こんにちは。究進塾 編者部です。

数学史の第3回-前編です。前回までの内容は、自然数、整数、商、無理数まで、数の世界が広がってきて「実数」と呼ぶところまできました。

今回は、虚数がどうして登場したのか、歴史的背景と合わせて解説していきます。

講師：新井康仁
日本大学文理学部数学科卒業 東京理科大学理学専攻科数学専攻修了
あるときは「分数の割り算」や「－×－＝＋」といった当たり前の概念を受け入れられない生徒に向けて、「実は数学者もそうだったんだよ！」と共感し、数学史を紐解きながら、数学者がどのように考えて、受け入れたか、を説き、またあるときは、数学の漫画や絵本を薦めて、生徒の数学への好奇心を掻き立てることに腐心する。「数学とは、すなわち考えること」を体現し続ける伝道師です。

前回の記事
【新井先生の数学史】第1回-前編 負の数を理解するまでの苦闘
【新井先生の数学史】第1回-後編 量の概念を手放した先とは？
【数学史第2回-前編-】四則計算のすべてで閉じる世界の創造
【数学史第2回-後編-】無理数の発見による最悪の結末

今回やること

前回、自然数のところから「マイナスっていう数を入れる」っていうところをスタートにしてたんですが、今回は数学者たちを何人か並べながら、数学者たちの時代と共に流れを追っていきたいと思います。

16世紀後半～17世紀

最初に出てきたのは「0-4」の話から出てきたパスカルさんなんですけど。

\ 第1回-前編に登場しておるぞ / パスカル（Blaise Pascal） ［1623～1662］ フランスの数学者・物理学者・思想家。パスカルの原理の発見が有名。著書は『パンセ』。

\ 第1回-後編にいました / デカルト （René Descartes） ［1596～1650］ フランスの哲学者・数学者。我思う、故に我あり。この人もマイナスの数が受け入れられない。

この人たちは17世紀の人です。デカルトさんは、今の数学で言うと、方程式の解をアルファベットの後ろの文字（ \(x\) や \(y\) など）を使いますが、最初に使い始めたのは、このデカルトさんなんですね。

それが出てくる以前は、ビエトさんっていう16世紀の人が使っていた記述方法がありました。

\ 数学は本業じゃないんです / ビエト （François Viète） ［1540年 – 1603年2月13日］ フランスの法律家、数学者。本職が忙しかった。1573年に最高法院ブルターニュ管区判事、1580-1584年はパリの最高法院の請願書審理官・王室顧問官を兼任、1589年以降アンリ4世に仕えるという多忙な人。スペインからの暗号文を解読したり。1564-1568年と1584-1589年は仕事がヒマな時期で、数学の研究に没頭。方程式の解法に詳しく、代数式の新しい表記を導入、一般係数の代数方程式を扱った人。

ビエトさんっていう人は、裁判官とか弁護士とかそっちの…全然数学と関係ないじゃんっていう人なんですけども、そういう人は結構多いんです。

元々この人が…今で言うと、「既知数」つまり「分かってる数」、それを母音を使って表しました。\(a\)とか\(i\)とか\(u\)とか。そして未知数を子音の文字、\(b\)とか\(c\)とかで表すっていうことをしました。

今の時代からすると、デカルトさんがやっている、アルファベットの最初の文字の部分を「既知数」として、アルファベットの最後の方の\(x、y、z\)みたいなやつは「未知数」として書くという、こっちの方が皆さんには分かりやすいかなと思います。

つまり今の学校の教科書っていうのは、このデカルトさんの作ったものに基づいて作られてるって思ってもらうと、「あ、この人すげえな」っていうのを感じるかなと思います。だから、ビエトさんは、あんまり学校の授業の中では出てきません。パスカルさんとかデカルトさんぐらいは出てくるかなと思います。

デカルトはどこで出てくるかっていうと、現代社会とか倫理とかですね。この人哲学者なので、そっちの方で扱われていることがあります。パスカルさんは「ヘクトパスカル」っていう気圧の単位で知られていますので、そちらの方でできますね。

そして1番、もう絶対知られていないと思うのは、ウォリスっていう人なんですけど。

\ イギリス人です / ウォリス （John Wallis） ［1616～1703］ イギリスの数学者。オックスフォード大学の教授。カバリエリやデカルトの考えを継承・発展させ、微積分学への道を開き、無限大の記号∞の導入なども。論理学にも業績を残し、暗号解読の先駆者でもある。

この人は、前回お話しした「数直線」を考案した人です。この人の著作『代数学』っていう本の中で、初めて数直線っていうものが登場します。

なので、それを元にしてデカルトさんが今度は「座標」、\(x\)座標、\(y\)座標ってやったと思いますが、それの原型になるものを作っていく。やっとそういう時代になってくるって感じですかね。

19世紀～20世紀

で、その次の時代です。「-1がどうして1なの？」っていう話をした時に「原点を置いて\(×(-1)\)っていうのが、ちょうど180°の回転する」いうふうな話をしましたね。あと\(+ (-1) \)っていうのは「逆方向の矢印が加わった足し算」ってやりましたけど。

第1回-後編で登場しました！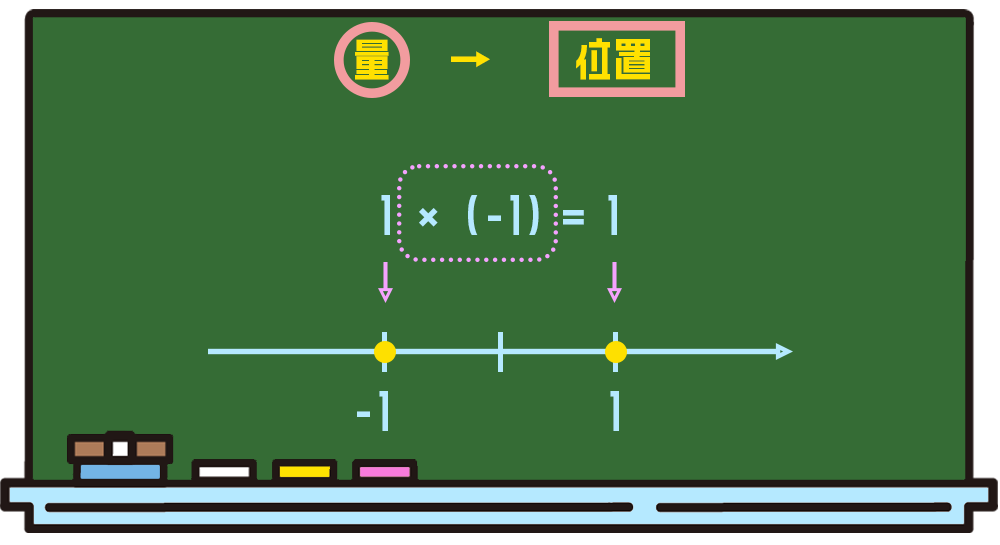
これは現代で言うと高校のカリキュラムで数学Cの「ベクトル」っていう内容です。矢印っていうのが出てきます。

「向き」と「大きさ」の要素が入ったものを「ベクトル」って言いますが、そこら辺の内容がちょうど入ってくるのが19世紀～20世紀あたりです。

だから、さっきの時代から、めちゃくちゃ飛んでるんですね。さっきまで17世紀だったのに、19世紀～20世紀の内容をやったりして。結構、時代を飛び越えながら「今やってる計算っていうのは、結局どういうことなんだろう？」というのを理解しようとしている、っていう感じです。

だから、ここまでで1回区切れるって感じですね。

新しい「数」の時代

ここまでの「数の世界」を、一緒におさらいしてみましょう。最初に自然数があって、その後は整数が乗っかってきて、有理数が入ってきて…と。

→→

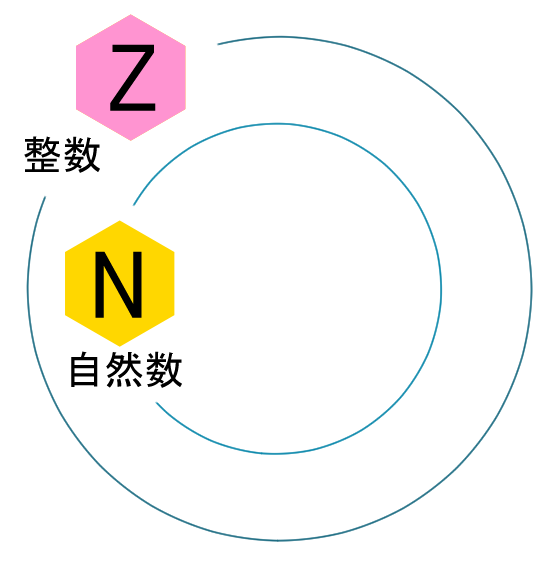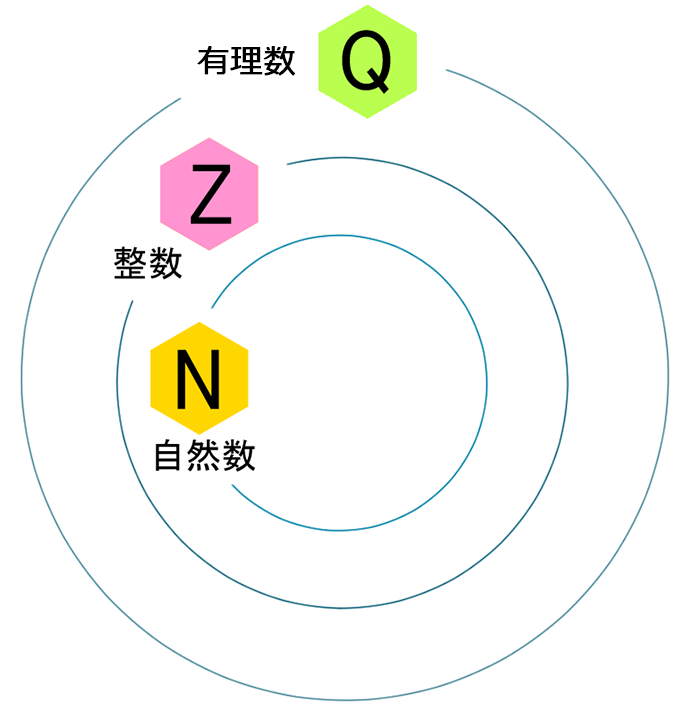
ここまでで「おそらく、これまで登場した数学者たちもなんとなく分かってくれるだろう」っていう数があったんですが、ここでちょっと時代を遡って…紀元前まで戻ります。

ピタゴラスさんの「ピタゴラス教団」のところで、ヒッパソスっていう人が「無理数」っていうのを発見してしまいます。

\ 認めません！ / ピタゴラス（Pythagoras） ［前570ころ～前496ころ］ 古代ギリシャの哲学者・数学者・宗教家。ピタゴラス教団を組織。永遠不変の真理を教える数学を重視し、「万物は数の関係によって秩序づけられる」と考えた。

\ だっておかしくないですか / ヒッパソス（Hippasos） ［紀元前500年頃］ マグナ・グラエキアに住んだとされる古代ギリシャの数学の研究者。無理数を最初に発見した人物であるという伝承が残っている。古代ギリシャ時代において随一の数学の研究機関だったピタゴラス教団のメンバー。

「√2」っていうやつですね。これが、\(a、b\)で、分数で書けないんだよっていうことが出てきました。式にするとこんな感じですね。

\(√2 ≠\frac{b}{a}\)

これを実際に発見した人、ヒッパソスを最後に紹介したという流れでした。数の世界としては、このように、「√2」っていうのは、Qの外側に、こんなふうにいます。

√2

有理数の世界に分類される数

で、他には実はまだ皆さんが知っている中だと…「円周率」って中学校で何て表しましたっけ。

πですね。πも今回、有理数の世界のところに入ってきます。

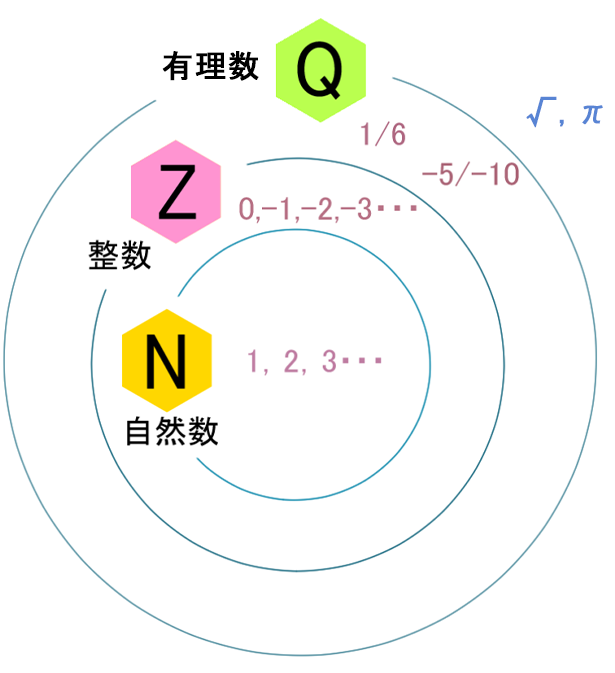
この他にも皆さんが知ってるもので、あとは「小数」があります。例えば0.1。0.1だったら分数に直せますが、何になりますか？

そうですね。\(0.1=  \frac{1}{10}\)ですね。では小数は、この3つの輪の世界だと、どこの輪に入りますか？

はい。なので、0.1は有理数のところに入ります。あと、小学校の時にやったかわからないんですが、例えば少数って言っても「1÷3」みたいなこういう割り算。これ、ちなみに「1÷3」って何になります？

そう。\(\frac{1}{3}\)を、実際に計算するっていう話になるんですけど、どうでしょう？

そうなんですよね。これ、0.333…って、この3がずっと続いていくんですけど、これ言い換えると「3が“循環してる”」って言うんですね。「3が繰り返される」っていう意味です。音楽の記号でそういうのありませんか？「繰り返し記号」って、ありますよね。数学にも繰り返す記号があるんです。高校の1年生で習うんですけど。

\( 0.\dot{3}\)

これ、0.333…という繰り返しを表す記号です。他にも例えば「0.123123123…」というのもあります。この場合は、繰り返しの「始まり」と「終わり」に点を打ちます。

\(0.\dot{1}2\dot{3}\)

これが。「1から3まで、ずっとこれが繰り返されますよ」っていう記号です。

一応、高校1年生で初めてやります。「数と式」っていうところでね。

なので、これみたいに、無限に続く中で循環される小数を「循環小数」って言うんですけど、無限に続く小数の中にも、繰り返されるものがありますよっていう。その循環小数も「有理数」に入ると。あとは、さっきの「0.1」みたいに、あるところで止まってくれる。これは「有限小数」って言います。有限小数も有理数に入ります。

で、さっき言ったπは、実は無限に繰り返される中で「循環しない小数」なんですね。3.1415…と続きますけれど、無限に循環はしないという。だから、そこがちょっと「有理数の仲間になるかそうでないか」っていうのを分けてしまう。

有理数の外側の数

ということで、この有理数の外側に「√2」とかがいます。「√2」は、教科書の後ろに√の表が載っかってるんですね。その表の、2とか3とかの列や行をダーっと見ていくと、1.14…とかって一応教科書には載っています。あんまり見ないと思いますけど、こういうのがあります。

で、この有理数と無理数を合わせて…何て言んでしたっけ？

そう、最後に少し出てきましたね。「ℝ」っていうやつを使います。これでもうちょっと数を広げたと。「ℝ」は「real」のRを使ってるんですね。なので、これは日本語では「実数」って言うんですね。「実際に存在する」って書くんですけど、「いや、どれも実際に存在してないだろう…」っていうツッコミを入れられるんですけどね。

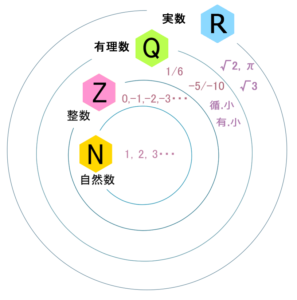
こんなふうに、自然数、整数、有理数、実数って言って、数をちょっとずつ…足し算、引き算、掛け算、割り算とかを自由自在にできるようにするために、どんどんどんどん 新しい数を、液体のように入れていって。で、その世界が「もう満杯になったよ」っていう段階で「じゃあ広げようとか」ってやってます。

数学者たちはこれを、食べ物とか飲み物で例えたりするんですけど…UCLA（カリフォルニア大学ロサンゼルス校）のエドワード・フレンケル先生が言うには「紅茶にミルクを入れた時に、こうやって広がるだろう？あれのイメージだと思えばいい」っていう、そういう話をしてて。

この0っていうのを自然数の世界のところに垂らしてあげると、自然数から整数の世界に広がる。だから、垂直線で言うと「左も考えていいよ」ってなるよねっていう。

そういう発想をしてるので、「白熱教室」っていうNHKの番組の中で、必ず食べ物を持ってくるんですよね。りんごとか、食べ物を持ってくるので、多分そういう感覚で数と向き合ってるんだろうなっていうふうに思います。

で、今こうやって「ℕ」「ℤ」「ℝ」「ℚ」っていう記号のパネルを用意してみてきました。「ℝ」が無理数なんですけど、無理数に対しては記号はあんまりないというか…当てないっていうのがあって。これは「ℚ」と「ℝ」を合わせて「ℝ」になってるので、逆に言うと無理数っていうのは「ℝ」から「ℚ」を除けば無理数が表せるっていう発想をします。なので、無理数にはちょっと記号がないということになります。

で、こんなことをやってくとですね、まだ広がるような感じがして。だんだん怖くなってくるっていうのが、数学者なんですよね。「いつまで、これどこまで広げるんだ」っていう話なんです。

表を使ってまとめてみよう

今やってきたことっていうのを、ちょっと表にしてまとめてみたいと思います。これも教科書数学の高校生がやる教科書に載ってるんですけれど、おそらくあんまり強調されないので。

	ℕ：自然数	ℤ：整数	ℚ：有理数	ℝ：実数
＋
―
\(×\)
\(÷\)

こういう表を用意します。まず、自然数（N）の世界の数の中から2つの数を取ってきた時に、足し算を行って、その結果ってどういう世界に含まれていたか？みたいなことを考えます。この試算を行った時、自然数の中に入っていれば「〇」と、記号書きます。

例えば…何でもいいですね。1と2を取ってきたら、\(1+2\)と試算してみて、答えは3。3は自然数の中に入ってるから、ちゃんとその世界の中で収まってる。…みたいなふうにしてちょっと表にしていきます。

こんな感じで、その世界の中で「足し算が閉じている」って言い方をするんですね。なんでもいいです。\(1+8\)とか\(10+12\)とかなんでもいいですけど、計算の結果がちゃんと必ずその世界の中で閉じていれば〇と書きます。

	ℕ：自然数	ℤ：整数	ℚ：有理数	ℝ：実数
＋	〇
―
\(×\)
\(÷\)

で、引き算の場合がこれが、できなかったんですよ。

\(0-4\)の計算をした結果は「0になる」という形で話が始まったわけですけれど「それだと矛盾が出てきちゃうよね」っていうことになりました。なのでマイナスの数が必要だっていうことで、自然数の中では閉じなかったのでこれは✕になります。

で、じゃあ割算は、掛け算はどうかっていうのも同じように考えていくと、成り立ってるのが、「足し算」と「掛け算」、この2つは必ず自然数の中のどの数を取ってきたとしても、足し算、掛け算は必ず自然数の中に入る。

で、割り算は、実は自然数も整数も、その中で閉じてくれないので…と、ダメなところを✕というふうにしていくっていう感じです。

	ℕ：自然数	ℤ：整数	ℚ：有理数	ℝ：実数
＋	〇
―	✕
\(×\)	〇
\(÷\)	✕	✕

こうすると、どこまでの世界だったら何ができるかっていうのが、この表から分かっていきます。こんなふうに〇をしていって。で、有理数の世界になっていくと、これ分数の世界なので、全部オッケーですね。

	ℕ：自然数	ℤ：整数	ℚ：有理数	ℝ：実数
＋	〇	〇	〇
―	✕	〇	〇
\(×\)	〇	〇	〇
\(÷\)	✕	✕	〇

ここに加えたものを書いていきますが、ℕとℤの世界の中に「0」「マイナスの数」を加えていって、でさらに、ℚとℝの世界に分数を加えていきます。

このとき、無理数が出てきた時に新しい記号としては、何の問題が出てきたかっていうと、「\(x^2 = 2\)は何ですか？」みたいなやつです。\(x^2=4\)、これはみなさんいけるんですね。2乗したら4になるxは何ですか？

そう、2。ところが今「マイナスの数もオッケー」となっているので、今では「2と-2」っていうふうに書いてあげます。

\(x^2=4\)
\(x=1, -2\)

これ、中学校3年生で初めて出てくるんですけど、「\(±\)」っていう書く方法があるんですね。

\(x^2=4\)
\(x=±2\)

同じ要領で言うと、\(x^2\)も\(±2\)って、なりそうなんですね。ところが、2乗したら2になるものなんて、このℕとℤの中に入ってないんですよね。で、ℚとℝの中にも入ってないんですよね。

…ってなったので、なんか反則的ですけど、こんなふうな「√2」っていう数を勝手に作る、っていうね。

\(x^2=4\)
\(x=±√2\)

「2乗したら2になるものはこういうふうに書きましょう」みたいな、そういうルールになりましたと。

ということで、は「√」っていう記号が入ってきたことによって「ℝ = 有理数」に加えたので、「数の世界を広げる」ということをしているっていうわけですね。

これで、合わせて実数になるので、もう全部できますよっていう。

	ℕ：自然数	ℤ：整数	ℚ：有理数	ℝ：実数
＋	〇	〇	〇	〇
―	✕	〇	〇	〇
\(×\)	〇	〇	〇	〇
\(÷\)	✕	✕	〇	〇

なので、

・ちょっとずつ何かを加えながら世界を広げてる
・どこまでだったら何算はできるのか？っていうのは、ちょっとずつ分かっていく

っていう感じです。だからなんとなく「もうこれ限界なんじゃないの？」っていうふうに、大体思うと思うんですよね。数学者たちも皆さんと全く同じ気持ちで計算をやっていましたから、まさかとんでもないものが出てくるなんて思ってないんですね。

だから時代をまた超えていく中で「こういう例が出てきましたよ」なんていうのを、ちょっと皆さんにお見せしていきます。

また新しいものが出てきた

それが、いつ出てきたのかっていうと、さっきデカルトさんの紹介をした時にも「17世紀」っていう話をしたんですけれども、この時は一応マイナスの数の計算はしてたわけですが、あんまりこう…全員が受け入れられたのかって言うとそうでもないし、デカルトさんも使ってはいたんだけど「いやなんかやっぱ気持ち悪い」みたいな。マイナスはやっぱり気持ち悪いみたいなふうに思っていました。

「でもあんた座標考えてんだから、マイナス気持ち悪いってどういうこと？？？」ってこっちとしては思うんですけど、それでも、デカルトさんもやっぱりマイナスは完全に受け入れられない…みたいな感じだったので。だからそうすると「もう自然数しか使えないじゃん」みたいな話になるんですけれど。

その中で、また変なのが出てきちゃうんですよね。

今…さっきのこれも十分変なんですけど。

\(x^2=√2\)
\(x^2=4\)

これ今、2乗したら全部プラスになってるじゃないですか。この例って、次に天才たちが何やらかすか、分かります？

今は2乗したらプラスになってますよね。ってことは、次に何やりたくなりますか？自分が子供だったら…って考えてください。

そうです。子供は逆方向へ行きますから、天才たちも逆方向に、今度は行きたくなるんですね。子供たちの方が天才になりやすいんです。逆に行きますから。もう常識はもう全部ぶっ壊しますので。例えば粘土で遊んでいて、何か作るものをやってて「これだったらこういうイメージでこれができるな…」っていうゴールが見えるわけですけど、あえてじゃあ水を変えてみようとか、絵の具を入れてみようとかっていうふうにした時に「何が生まれるだろう？」って考える子どもに似てる。天才たちは、そういう発想をしています。

じゃあやってみようっていう、そういう話です。

なので、またとんでもないものを考え始めるわけですね。「じゃあ2乗したら-1になるものって何だ？」というのを考えたら、何が生まれるんでしょうか？さっきのルールと同じような発想をする、っていうところは、できそうなんですね。

\(x2\)が2、これの場合は\(x=\)…もう1回。何でしたっけ。

ってことですよね。じゃあ同じ発想で、これ何者かは今分からないですが、分からなくても何かできそうですよね。\(x^2=2\)のときを真似すると、この時は何をしました？

そう。\(√\)をつけて、\(±\)をつけたんですよね。同じことしたら、どうなります？

それだけなんです。試そうと思ってるのは「同じことをしてみよう」なんです。

「\(\pm\sqrt{-1}\)ってなりそうなんじゃないの？」とかってなるんですね。これは別に自然ですよね。元の\(\pm\sqrt{2}\)の方が不自然なので。

「なんかこれが出てきたはいいけど、じゃあこいつが一体何者なのか」っていうのを、どうやって受け止めていくのかっていうことになります。

数学って変！

だから、数学のやっぱり変なところは、計算はできてしまうっていうのがあって。

だから計算自体は先に進んでいっちゃうんですよ。こっちは意味わかってないのに、「いや、俺たちはもう先に進むから」みたいな、勝手に進んでいっちゃうので。

これがすごく不思議なんですよ、数学やってると。

「これに何の意味があるんですか？」ってすぐ言いたくなるんですけど、世の中がまず安定しすぎちゃってるっていうのがあって。

数学は全然もう不安定なんで、行きたいところに勝手に動いていくっていうのがあるんですよね。

宇宙と似てるかもしれないですね。

ここまでの時代のまとめ

だから、ここからの時代はものすごく長いんですけど、これ今ちょうどやってるのが、17世紀とか16世紀の時代です。

計算はとにかくできるんだなっていうところで。

この後出てくる天才たちも「計算はもうとにかくこれできちゃうわけだから、何か矛盾が起こらなければやっていい」っていうのがあるので、「計算してなんか答えが出ればいい」みたいな感じにはなるんですけど。

でもやっぱり、さっきのデカルトさんじゃないですけど「マイナスの数はなんか気持ち悪いよな〜」っていう、その引っかかりだけはどうしても残ってしまうっていうのはあって、そのまま200年ぐらい過ぎます。

よく200年も耐えたなっていう。やたらと耐えるんですよね。

で、そこら辺で、時代的にはルートが出てきます。高校生だとルートが出てくるのは、高校2年生ぐらいの「複素数」っていう単元で、一応習います。

で、高校生の2年生の授業でも、あんまりそこの意味に立ち入った話をしてしまうと、結局もっと深く深く勉強しなきゃいけなくなっ ちゃうから「計算できればいいよね」っていうふうに、教科書も構成されちゃってるんですよね。

だから「計算できるからいいか」みたいなふうにして、学校の授業は進んでしまうっていうのがあって。そこはもったいないなっていう感想はちょっと持ってて。

なので、せっかくなんだから「これがどういう意味だったら、もうちょっとその近くにいられるか」っていうのを分かった方がいいよねっていうことで、一応歴史的なことをお話をするんですけれど。

意味を考えてみよう！

これは今、フランスとかの話なんですけど、舞台を移して、今度はイタリアです。

16世紀のイタリアになるんですけど、その中で初めて本に出てくるんですよね。イタリアの数学者で「カルダノ」っていう人なんですね。

\ 医師ですが占いもやります / カルダノ（Girolamo Cardano） ［1501～1576］ イタリアの数学者・医者・哲学者。カルダーノの公式とよばれる三次方程式の根の解法を発表。

カルダノさんは、お父さんがレオナルド・ダ・ヴィンチの親友っていう、一応有名な人なんです。この人の職業が、本業は数学者ではなくて医者なんですね。

結構多いんですよね。弁護士やったり、裁判官やったりして、暇な時間は数学やるっていう人が多くて。「何で暇な時間に数学やるんだよ」って話なんですけど。

もっと経歴をたどってみると、占い師をやったり占星術をやったり、あと賭博師をやったり。しかもこの人、最後は自殺っていうか⋯自分が死ぬ日を占って、その日まで何も食べないで餓死して死ぬんですけど。自分で決めてその日に死ぬっていう、なんかちょっと変な人です、この人。

で、一応こういう人が『アルス・マグナ』っていう自分の著作物に、初めて「\(√\)の中にマイナスが入ってくる」っていうものを載っけるんです。

その中に「10っていうのを2つに分割して、掛け算は40になるようにするには、その2つってどうなればいいの？」っていう問題を載っけるんですね。ちょっと式で書いてみますね。

\(a＋b=10\)
\(ab=40\)

\(a\)と\(b\)を2つにして足したものが10になって、かけたものが40になる。こういう\(a\)と\(b\)は何になるの？っていう、数遊びみたいなやつです。

これを解いた時に出てくるのが、結果として

a = 5+ √-15, b = 5- √-15

っていう。こんなのが出てくるんですね。で、この「\(a\)と\(b\)を10にする」っていうのは、線分の長さで言うと、線分があった時に2つに分割するんですが、別に当分の話をしてなくて、とにかく「分ければいい」っていう話の問題になって考えてたんですよね。均等の長さで分ける必要はないんです。

だけどこの時代って、パスカルさんの時にも話したんですけど、量の概念から抜け出せないっていう時代なんですよね。「マイナスの数なんてないんだから、考えてもしょうがない」って考えてた時代なんで。

だからそう考えると、\(5+√-15\)って長さなんですよ。カルダノさんにとって見ると。

\(5+√- 15\)cmって何なんですかって話なんですよね。

だから、一応答えとしてはこんなのが出てきたんだけれど、「この数自身にどういった意味があるのか」というか、意味っていうのが見出せないっていうか、その使い道っていうのはないんじゃないの？っていう。

この「√」っていうものっていうものは、「存在しない数」という意味を込めて、さっきのデカルトさんは「虚数」って呼びました。英語だと、「imaginary number」っていう。「imaginary number(想像上の)」の頭文字の「i」を取ります。

今回、ルートの話の最初に「\(√-1\)って、何なんだ？」みたいな話になりましたけど、今の学校の教科書だとこの「√-1」を「iと表記する」となっています。これはデカルトさんが最初に「imaginary」と言った、頭文字の「i」を残してるんですよね。

「こんなの存在するわけないでしょ」って言ってたのは、ピタゴラスさんも言ってました。「ルートなんて存在するわけない」って。新しい数が出るたびにみんな言うんですよ。「こんなのいるわけないでしょ」って言うのは一緒なんです。それを「じゃあどうやって乗り越えるのか」「じゃ、意味付けってどうしたらいいのか」みたいな話が今後出てくる、と。

で、ここから、この虚数って言われるものに対して、実はそのまま通り過ぎてもいいんですけど、見て見ぬふりができなくなってくる、っていう事態がきます。

やっぱりそういう出来事がないと、みんな素通りしていってしまうっていうのはあるんです。

〈後編へ続く！〉

動画バージョンはこちら↓