こんにちは。究進塾編集部です。

今回は、無理数についての解説です。前回は四則計算についてのでしたが、無理数の発見による最悪な結末とは一体？「新井先生の数学史 第2回-後編」です。

講師：新井康仁
日本大学文理学部数学科卒業 東京理科大学理学専攻科数学専攻修了
あるときは「分数の割り算」や「－×－＝＋」といった当たり前の概念を受け入れられない生徒に向けて、「実は数学者もそうだったんだよ！」と共感し、数学史を紐解きながら、数学者がどのように考えて、受け入れたか、を説き、またあるときは、数学の漫画や絵本を薦めて、生徒の数学への好奇心を掻き立てることに腐心する。「数学とは、すなわち考えること」を体現し続ける伝道師です。

前回の記事
【新井先生の数学史】第1回-前編 負の数を理解するまでの苦闘
【新井先生の数学史】第1回-後編 量の概念を手放した先とは？
【数学史第2回-前編-】四則計算のすべてで閉じる世界の創造

三平方の定理

「皆さんと数学者って、そんなにかけ離れてないよ」っていう話をしたんですけど、皆さんが知っている数学者の中で、「ピタゴラス」という人がいますが、まさにピタゴラスという人も「全ての数は全部有理数で表せるよ」というふうに言ってたんですよね。ということは、他の数出てきたらやばいなっていうふうになってくるわけなんですけど。

実は、皆さんが中学校の3年生で習う図形の問題の中で「三平法の定理」というのが出てくるんですよね。「三平方の定理」って覚えてますか？

「平方センチメートル」とかって言いますよね。「平方」って、「\(cm^2\)」と書きますよね。だからつまり、この小さい「2」を「平方」って言ってるわけです。これ、「平方」を初めて中学校でやるのにも関わらず、小学校で「\(cm^2\)」を教えるっていうね。

「三平方」の意味っていうのをちゃんとやると、「同じものを2回掛け算する」っていう意味です。

分かりやすい例で言うと、「3の2乗」って「\(3^2\)」と書くんですけど、これは「3×3」＝「3を2回掛け算している」という意味なんですよね。だからこれは「平方数」と言ったりします。

だから、三平方っていうのは、まさに「3つの何かが平方されている」ということです。「図形に関するもので、3つの何かが平法されてる」っていうふうに聞くと、何か想像できますか。

皆さんが知ってる図形って何がありますか？

そうですね。三角形の中でも、いろんな三角形がありますよね。「〇〇三角形」ってありますけど、そういう三角形って何が思いつきますか？

そうですね。そのようにいっぱいある中で、実は直角三角形って、かなり特殊な直角三角形の種類なんです。こういう形の三角形ですね → ◢

で、「直角」って昔の人にとって、すごい大事なんですよね。なんで大事か分かりますか？生活を考えると分かるかもしれないですね。

そうですね、傾いてたらやばくないですか？

あとは、昔の人って「縄を張って、比を測る」っていうことをやってる人がいて。「縄張り師」っていうんですけど。あとは、今でも「縄張り」っていう言葉が残ってるんですけど、「俺たちの縄張り」みたいな。あれって広さを表してるんですよね。それぐらい面積とかに関わってるから、生活に密着してるっていう意味では、直角はすごく大事になってくるということなんです。だから多分、直角三角形を研究したんだろうなっていう。

三平方の定理は、実は直角三角形に関係している定理です。「三」って何かって言うと、これは「3つの辺」の話をしています。

例えば、3つの辺をそれぞれ\(a,b,c\)としてあげます。

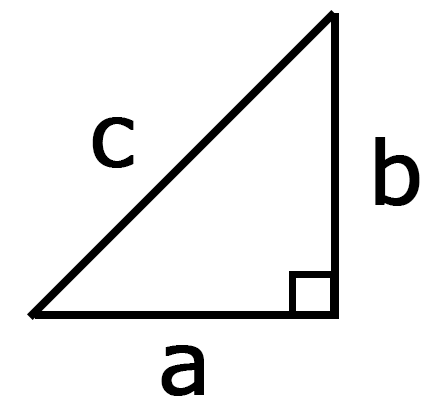
1番分かりやすいのは、昔の人が使ってたのは、3と4というやつですね。

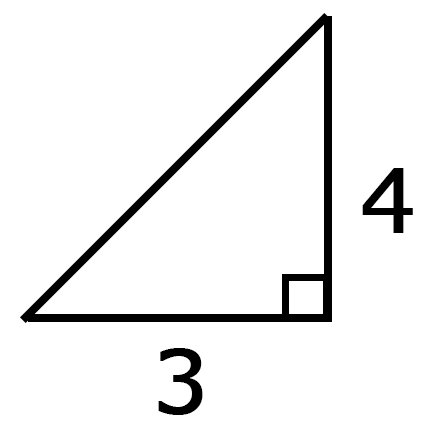
三平方の定理っていうのは、この直角を挟んでいる2つの辺（3と4の部分）の2乗だから、\(3^2\)と\(4^2\)。この2つを足したものが、辺cの2乗になる。これを「三平方の定理」って言います。

計算してみると、\(3^2+4^2\)は\(25\)になるので、\(3^2+4^2=5^2\)となります。辺cが分からなかったとしても、直角を挟む2本の2辺が分かれば長さが出てきてしまう。こういう定理があります。

そうすると、3、4、5ぐらいの数だったら、前回のこの輪から外れていないので、よかったんですよね。ピタゴラスさんにとってもよかったんです。

ところが、なんと弟子が「こういう例があるんですけど、これどうしたらいいんですか？」みたいなものを、持ってきちゃったんですよね。

今までの輪から外れたもの

それがどういうものかって言うと…さっき「正方形」っていう言葉が出たので、正方形を用意します。

正方形だと長さが全部等しいので、1番簡単な正方形を書いてみます。

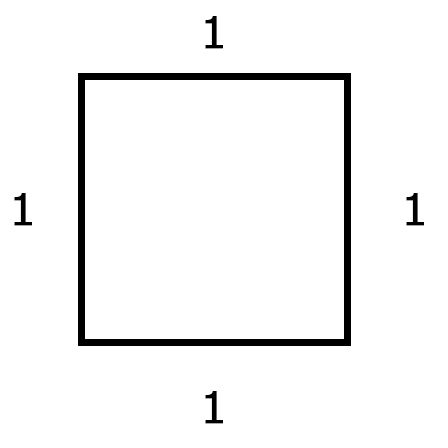
1番簡単な正方形は、一辺が1の正方形が1番簡単です。長方形とか正方形って、面積測る上での計算式は、1番みんなが分かりやすい「縦×横」なんですけど、実は面積を測るっていうのが、実はこれ英語の語源にもなっています。「幾何学」っていうものを英単語にすると「geometry」っていうんですね。

この単語を区切ってあげると分かるんですけど 「geo/metry」、こうやって区切るんですね。すると「geo」というのが「大地/土地」って意味ですね。で「metry」は「測る」という意味です。だから「土地を図る」ことから「幾何学」という言葉が出てきたんです。

紀元前とかで言うと、ナイル川が毎年決まった時期に氾濫してしまって、みんなの家とかを流してしまう、そういう時期があったので、測量しておいて自分たちの土地がどれぐらいかっていうのを、どうしても測っておく必要があるっていうところから、この言葉が生まれたっていうのが歴史的な背景なんです。

ピタゴラスの弟子にヒッパソスっていう人がいるんですけど。

ヒッパソス（Hippasos） ［紀元前500年頃］ マグナ・グラエキアに住んだとされる古代ギリシャの数学の研究者。無理数を最初に発見した人物であるという伝承が残っている。古代ギリシャ時代において随一の数学の研究機関だったピタゴラス教団のメンバー。

その人が、この1番有名な正方形、一辺が1という正方形の、対角線をこう測ったんですね。

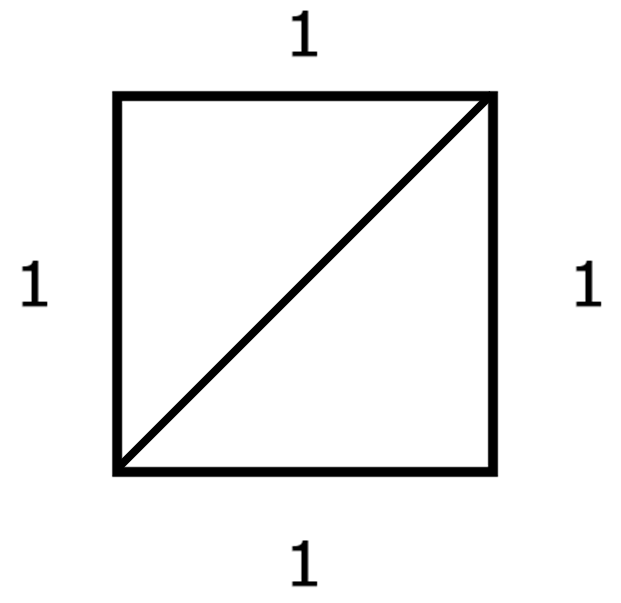
その時にですね、この対角線、分かんないじゃないですか。今の長さだと。分からないから、この対角線を\(x\)にしておいて、実際にちょっと三平方の定理を使ってみましょう。

どうなるんでしたっけ、三平方の定理って。

はい。\(1^2+1^2=x^2\)。そうなんですよね。これは計算すると何になりますか？2ですよね。\(x^2=2\)となりますよね。ということは、さあ、なんか久しぶりに出てきましたね。2次方程式ってやつです。ここで2次方程式が出てくるんですね。

(笑) これ、\(x\)にすると難しく見えるってことですよね。なので\(x\)と見ないで、じゃあ四角だったら難しく見えないですかね。\(□^2=2\)としましょう。2回かけたら2になる。元は何ですか？と、言ってるんですね。

だから、さっきで言うと\(3^2=9\)だったよねっていう話を振り返ると分かるんですけど、9という方が先に分かっちゃってて「解の方から3の方を出して」って言ってるんですね。

そうすると、今は2を考えてるんだけど、今はひとまず復習で、解の部分に4と置いた方が分かりやすいかなと。2回かけたら4になるもの。これは思いつきますか？

これ、2ですよね。だって2回かけたら4になりますよね。だから「2」って見つかるんですけど、これ今やりたかったのは、解の部分が2なんですよね。ってことは2回かけたら2になるものって、今までの輪の中にあるんですか？という。そういう問題が出てきちゃいます。

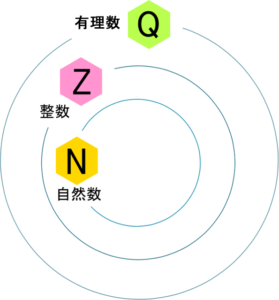
だって、この世界の中で計算してるんだから、ℕかℤかℚの世界に数が存在しないと計算できないんでしょ？って。みんな「自然数の中にあるかな」「整数の中にあるかな」「有理数の中にあるかな」っていうのを、ピタゴラスさんの弟子は皆さんと同じようにやりました。

「ない」ってことは、「じゃあ…ピタゴラスさん間違ってるんですか？」「有理数までしかないって言ってたじゃないですか！」「だってないんだけど…」とかってなっちゃって。

「じゃあ、こいつ…一体何者なんだろう」みたいな。

「自然数、整数、有理数でないもの」というのは、おそらく小学校の数の中で扱ってきたイメージからすると、まず「想像ができない」っていうのありますよね。だから数学って、想像できないものに対して「新しいものを想像してください」って言ってくるんですね。数学側が要求してきますっていう。「無かったら作ればいいじゃん」とかね。

そういうところで要求してくるものだから、そういうところで「なんか嫌になってしまう」ってのはあると思うんですけど。逆に言うと、皆さんに権限を与えてくれるんですよね。「なきゃ作ればいいじゃん」って言ってくれるわけですから。

ということで、2乗したら2になるものっていうのを「じゃあ記号で当てよう」っていうふうな発想になります。その記号というのが、中学校でやる「√2」っていうやつです。これ、なんか反則なんですよね。「2乗したら2になるものなんて無い」って言ってんのに「じゃ、なきゃこれ作ればいいじゃん」って。それズルくないですか？

ということでこいつが出てきたわけなんですが。

勝手に作ったはいいわけなんですが、この√2が、まずここの「ℕ」「ℤ」「ℚ」の中にいるかどうかが、まず全然分かってないんですよ。分かってないからどうするかっていうと、じゃあこのヒッパソスっていう人と同じように、一旦ピタゴラスさんを上に立てておいて。師匠ですから。

じゃあピタゴラスさんの言うように、有理数としてみようかと。よくわかんないけど。てか、よくわかんないんですよ、まずこの段階だと。この\(x\)というのを√2って書いたものの、そもそも√2が実体がよくわからないので、結局分からないんですよね。

だから、それまでの数の中で、今は限界が有理数になっちゃってるから「一旦こいつを有理数として話を進めてみたら何か見えてくるかもしれない」っていうふうに考えます。

数直線を考えた時、その手前の時に、パスカルさんが0-4を一旦0として、その後に「足し算が成り立たないからやっぱダメだよね」って発想したのと一緒で、一旦進んでみるっていう。

進んでみると何か分かるかもしれないっていう発想するんですよね。だから、そこら辺は数学者は柔軟だなというか、自由だなっていうのはあります。

ヒッパソスと同じことをやってみる

次にやりたいのが、ヒッパソスさんがやったことを、ちょっと皆さんで体感しようっていうのをやっていきたい。

問題を1個用意しました。この人がやったことなんですけど「√2」っていうのがおそらく「有理数の世界の数ではないんだろうな」っていう予想ですね。

予想で今は皆さんが高校の中で1年生で習う言葉の中で有理数に対して、…ま、「有る」の反対なんですよ、結局は。

「有るの反対だから何ですか？」っていう。そう、「無い」ってことなんですよね。だから有理数に対して無理数っていう話が出てくるわけですけど。これ高校生に話すと「無理だから無理数」とかって冗談を言い始めるんですよね…。(笑)

この段階だと、今これが無理数かどうかっていうのが分かってない段階で、このヒッパソスっていう人が「じゃ実際にピタゴラスさんが言うように、有理数なんだったらちょっと有理数として話を進めてみるっていうのが1番いいよね」っていうことで。

話の進ませ方としては無理数っていうことがよくわかんないから、無理数って言ったところで式にはできない。式にできないんだったら、式にできるような形を取ろうっていうことで。

有理数って分数ですよね。分数って、もう1回聞きますが、どんなものがありますか？具体例で。

そうですね。これ、小学校でやるのが、例えば4/6とかになってたら「約分しなさい」って言われますよね。

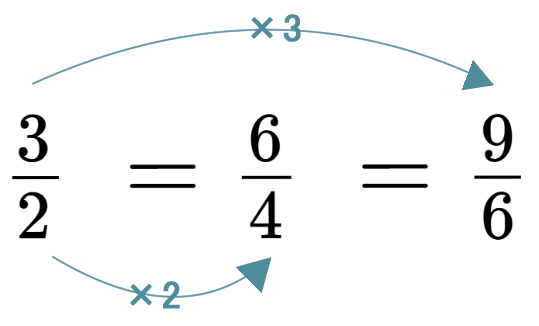
こうすると結局、全部一緒になっちゃう。約分ができる状態の分数って無限に出てきちゃうので、それだったら最初から約分がされてる分数を数えてしまえばいいよねっていうことで。

この「完全に約分されたもの」を、「すでに約分された分数」ということで、「既約分数」というんですね。漢字が難しいですよね。でもこれ、高校1年生で出てくるんですけど、分母と分子で「もうこれ以上約数がないよ」というふうにも言ってもいいですよね。「分母と分子は、最大公約数は1ですよ」というふうに言ってもいいです。

高校生向けにもう1個だけ言っておくと、分母と分子は「互いに素」という言い方をします。これは「最大公約数が1です」っていう意味と同じです。「分母と分子を割るのに、1番大きい数で割れても1だよね」っていうのを示す、こういう用語があるんですよ。っていうのは、もし高校生が見てる時に「なんかこんなの習ったな」っていうふうに思ってもらえればいいかなと。

で、実際にこの具体的な数字をいくつか見せても、証明というか…説明がちょっとなかなかできないので…皆さんここから1個我慢をしなきゃいけないところがあって。ちょっと文字を使わないといけないよねっていう。

文字…

話の進め方は、ピタゴラスさんがっているように「√2が有理数である」として話を進めてみましょう。そうすると分数だから、「\(\frac{〇}{〇}\ \)」っていうふうに表せるよね、ということで、例えば何でもいいんですけど、

\(√2= \frac{b}{a}\ \)

\(a\)と\(b\)みたいなものを使う表現できるっていう。ここら辺でだだ嫌になっちゃいますよね。(笑)

文字出すのはなぜかというと、具体的な例だと何か違う例を上げられちゃうと困るから。色々なパターンが出てきちゃうから、何か一般的なもので話を進めようってことなんですけど。

で一応、もうこれ以上約分できないよっていうことで、aとbはさっき言った「互いに素な自然数」っていうっていうふうに表せます。でも、このまま「何かをしなさい」って言われた時に、なんかこれ…何していいかわからないので「分数ちょっと邪魔だな」っていうところだけはあります。

これ\(a\)がちょっと邪魔なんですよね。\(a\)が邪魔なので、分数をちょっと消したいっていう時に、どうやったらこの\(a\)が消えてくれますか？

そう。これ、分数というのは\(a\)が割られてるので、逆の発想で\(a\)をかけてあげれば、どっちも消えてくれます。なのでどっちにも\(a\)をやってかけてあげると、約分されて消えます。

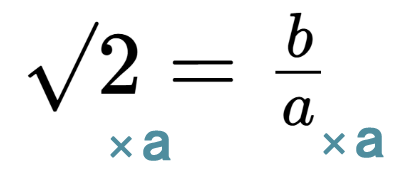
そうすると\(√2a = b\)ってなりますね。「これ…だからどうした」って話なんですよね。(笑)

で、結局そのヒッパソスが言ってることっていうのは「どこかで、何かが、おかしなことが起こる」ってことを、ピタゴラスさんに最後言いたいんですよ。

何かがおかしいって言っても、何がおかしいかはちょっとやってみないとわからないので、この式変形であと何ができるかっていうのやるんですけど。やれることは、あとは「両辺を2乗する」っていうのができるんですね。

さっきやった「\(x^2 = 2\)」になるっていうやつの\(x)のところが、この√ 2。ということは、2乗したら2に戻るだけです。

2乗したら2になる元々がこれだったから「\(√2\)の2乗が2」っていうことなわけなのでね。なので、元々√2ってことは、2乗してあげると\(√2a = b\)の√2は2に戻って、\(a\)が2乗されます。\(a\)は2乗されると、ただ上に2がかかれるだけです。

そうすると式は\(2a^2 = b^2\)。両辺を2乗してあげるとこうなります。

で、この式変形を進めていって、数学者たちって何に…関心というか注目をしているのかっていうと「何かの倍数とかになってたら、なんか特徴見えないかな」とか。時計もそうですね。12の倍数になってるとかっていうふうに捉えると発想と似てるんですけど。

これの場合って、\(a^2\)はちょっとよくわからないけど、ここに2が掛け算されてるっていう、こういうところ着目したりするんですよね。

「\(2a^2\)」の部分ですね。

中学校で「偶数を、文字を使って表しなさい」っていうのをやるんですよね。1番いいのは、2、4、6とかってありますよね。あれの「特徴的なものは何なのか」っていう。2、4、6、8、…、これこのまま見てるだけだと、なかなか「特徴って言われても…」って感じになっちゃうので、これを次のように書き直すんですね。

\(2×1、2×2、2×3、2×4、\)…

そうすると、これ全部に何がくっついてますか？そう。\(2×、2×、2×、2×\)…というふうになってて、偶数の特徴は「全部2が掛け算されている」っていう。なので、\(2a^2 = b^2\)の「\(2a^2 \)」って、これ偶数になるんですね。

aの2乗が分からなくても「偶数になる」っていうことが分かれば、数学者は細かいこと全然気にしないんですよ。すごいんですよね。普通、僕なんかからすると、なんか細かいことの方が気になっちゃうんですけど、数学者は「2を見つけたから、これ偶数だから、どうでもいいか！」みたいな感じになっちゃうので。

だから、これ偶数なんですよね。ということは右辺の「\(b^2\)」も偶数なんですよね。イコールで結ばれているから\(b^2\)も偶数になります。ってことは、2乗して偶数ってことは、元々は？

やっぱり偶数ですよね。

例えば\(2^2\)が4っていうのを考えるといいんですけど、そうすると今分かったことは、これ\(b\)は偶数って分かるんですね。\(b\)が偶数って分かるとこっちが偶数なので、今\(a^2\)には全然着目してなかったんですけど、\(a^2\)も分かっちゃいますね。

\(b^2\)が偶数、左辺には\(a^2\)の前に2がありますよね。その2と右辺、偶数で割り切れますよね。ちょっと計算だけちょっとだけやります。1個だけ文字を使ってあげると。\(a\)と\(b\)をさっき使ったので、\(c\)と置いてみます。こうしてあげると、\(c\)の細かい実体は分からなくても、「自然数になってて、偶数だな」っていうふうに思ってもらえればいいです。

そしたら、これをこの中に…代入って覚えてますか？「文字の中に文字を入れる」っていう。

これは実は、17世紀の数学者たちも初めてそういうことをやり始めたので、その前までは数字を当てはめるだけだったんですけど、「文字の中に文字を入れる」っていう発想はしないんですよね。ま、気持ち悪いっちゃ気持ち悪いですけど。

なので、そこの部分をやってもらうと。\(b=2a\)、これを\(2a^2=b^2\)に入れてあげます。なので形で言うと、\(2c\)の塊の2乗ということですね。

\(b\)：偶数より
\(b=2c\)
\(2a^2={(2c)}^2\)

すると、\({(2c)}^2\)は2×2で、c×cと2回掛かってるので、\(4c^2\)で、ここ2aの2乗です。そうすると左辺に2、右辺に4があるので、約分ができます。そうすると約分できます。

\(2a^2=4c^2\)
\(a^2=2c^2\)

そうすると、こうなるんですね。ここ、今\(c^2\)が分からなくても良くて「ここって結局偶数」ってことが分かればOKです。

ってことは、\(a^2\)は偶数なんですね。
ってことは、\(a\)も偶数なんですね。
ってことは、今分かったのは、\(a\)と\(b\)って、どっちも偶数なんですよ。

これ、最初に「何を出発にしたか」って言うと、「\(a\)と\(b\)って最大公約数が1」なんですよね。\(√2=\frac{b}{a}\)の、\(a\)と\(b\)は「互いに素」、最大公約数が1です。

そうすると「1番大きくても1でしか割れない」って言ってんのに、\(a\)と\(b\)は今何が分かったかっていうと、「\(a\)と\(b\)は偶数」なんですね。偶数ってことは、1番大きく…っていうか、少なくとも何で割れるんですか？

そう、2で割れちゃいませんか？っていう。「1番大きくて1だ」って言ってましたよね、最初。だけど、これを仮定して話進めてしまったことによって「2では最低限割れちゃう」と。

じゃ最初のこれ、「互いに素」っていうのは、どうなんの？っていう。ということで、矛盾になっちゃうんですよ。だから「分数で表せる」として話を進めると、「互いに素」と「偶数である」が矛盾してしまうんですね。

だから「最初に仮定していたことが誤りだった」っていう話になるんです。ということで「√2はやっぱり有理数ではないんだな」っていうことが分かるんです。いやでも無理数が分かったとは思えない…とか思いますけどね。(笑)

新発見によって起きた悲劇

こういう感じで、これをヒッパソスがピタゴラスさんに持っていったら、ものすごいショックを受けるわけですね。当たり前ですよね。自分が信じたものを覆されるんですから。

で、このことを「ちょっと秘密にしろ」っていうことを言ったっていうのが、伝説で残ってるそうです。ま、伝説なので真実は知らないですけど。大丈夫なのか？この教団…。(笑)　そういうことがあって、その後に結局バレてしまって、ヒッパソスはエーゲ海の海に沈められたとかなんか、色々な話が残ってるんですけど。

そんな感じで、たった1つの発見が「え、人殺すの？」みたいなところに繋がっちゃってて。「ピタゴラスさんはいいところ、いい面も産んでるのに、なんかすごい怖い面も産んでるな」みたいな。大丈夫なのかみたいな。

だから今後、新しい数を発見するたびに、みんなが「いやちょっとこれ発表しにくいな…」「殺されるかもしれないし…」みたいなふうになってくるんじゃないかなっていうのはあるなって思ってて。

これは高校の教科書で言うと「発展」とか「研究」っていう項のところに書かれたりすることもあるし、「こうやって仮定するとこうなってこうなって…で最初と矛盾するでしょ？」という論理の部分も結構見れてしまいます。

僕が授業でよく話をするのが、「数学って法律に近いね」って話をするんですよね。ある種、条例とかを決めてしまって、もう1個の何かを作りたいってなった時、「こっちの条例に反しないようには作らないといけないじゃん」とかって。だから法学者とかは数学をやる人っていうのが結構多いよね～、とかって話をするんですよね。

なので、実は後でまたアマチュアの数学者で「フェルマー」っていう人を紹介するんですけど、実はこの人は数学者というよりは裁判官とか弁護士なんです。そういう人も後で出てきます。

ということで、今回は自然数、整数、そして有理数。で、最後に出てきた、後に無理数というふうな名前になるわけですけど、それで新しい世界を拡張させて合体、これ実は「実数」っていう世界になります。実数っていう、英語で言うとそのまま「real number」といいます。これは普通ですね。なので記号では「ℝ」の二重線で当てたりします。

ここら辺までを今日は紹介して、次回はもしかしたら二次方程式の方に行くかもしれないし、数をどういうふうに広げようかなというふうに思っていますので、また次回をお楽しみにしてください。

動画をご覧になりたい方はコチラ！↓