こんにちは。究進塾編集部です。

今回は、四則計算についての解説です。自然数、整数、有理数を「閉じる」とは？数の世界をさらに広げる、「新井先生の数学史 第2回-前編」です。

講師：新井康仁
日本大学文理学部数学科卒業 東京理科大学理学専攻科数学専攻修了
あるときは「分数の割り算」や「－×－＝＋」といった当たり前の概念を受け入れられない生徒に向けて、「実は数学者もそうだったんだよ！」と共感し、数学史を紐解きながら、数学者がどのように考えて、受け入れたか、を説き、またあるときは、数学の漫画や絵本を薦めて、生徒の数学への好奇心を掻き立てることに腐心する。「数学とは、すなわち考えること」を体現し続ける伝道師です。

前回の記事
【新井先生の数学史】第1回-前編 負の数を理解するまでの苦闘
【新井先生の数学史】第1回-後編 量の概念を手放した先とは？

「0」という数の不思議

0っていう数って「不思議だな」って感じることってありませんか？何が不思議なのかっていうと

・足しても変わらない ・かけたら相手を0にしちゃう

っていうのはありますよね。特に、相手がいくら強かったとしても「相手を0にしてしまう」っていう。0って、そういう強さがあります。だからもう「0って強いな」っていうところが1つ。

あとは、掛け算はできるけど、実は割り算って⋯例えば小学校で「0で割る」っていうことをやってるのかな？っていうのを、ちょっと振り返ってみたいんです。

たぶん「0÷2」っていうのは、これはやってると思うんです。「0÷2」って、どういうふうに考えます？

そうですね。この場合だったら「個数」で考えて、いけそうですよね。前回のことを振り返るとわかるんですけど、割り算の反対って何算ですか？

掛け算ですよね。ということは、これ、元に戻ればいいから、「0×2」でちゃんと0に戻るから「ああ、なんかいけそうな感じがする」っていうことなんですけど。

じゃあ、逆にしてみましょうか。

「2÷0=？？？」

ここが一番、厄介なことが起こるんですよ。

今、割れないって言ってくれてよかったです！「割れない」ということは、つまり「この計算は、なんかできなさそう」って思ったってことですよね。

実はそれ、正解なんですね。

「計算せよ」って言っておきながら「計算できません」っていう問題って、多分ないと思うんですよね。まさにそれが初めて、中学校で出てきてしまう。

小学校では「計算できるから計算しなさい」って言ってるわけですけど、中学校の場合は「できないこともある。だけどじゃあちょっと調べてみて」みたいな。

？？

「え、じゃあこれ何なの？」っていうことなんですよね。

それで、教えていたりすると「え？0/2って0だから、じゃあ2÷0も0じゃないですか」ってふうに言ってくる子がよくいます。そういうときには、一旦0にしてしまって、後で考えればいいっていうやり方をします。

だからこれは0にしてしまおうと。

「2÷0=0」

としてあげると、確認するには逆を操作してあげればいいってことですよね。「0×0が2に戻るか」って考えてあげると戻らないわけですから、だから前回のことと、結局繋がっちゃうんですよね。

前回の内容というと、0-4がわからないから、最初は「まあ0なんじゃないか」っていうふうな話を進めていたわけですけど、0+4は0にならないわけですから、だからじゃあこいつは何なんだっていうところから「？」になって。

元に戻るためにはどうすればいいかって言ったら「そもそも意味がわからないんだから、量の話は無理だよね」っていうことで、意味を変えてあげて出てきたのが「数直線」ですよね。

「0-4」の式にある「マイナス」というものが「“向き”を持ってる」というふうに捉える、という感じです。向きを持っていると捉えると、矢印が右方向へ向いているときには「右に行けば行くほど大きくなる」というふうになります。

なので、今度は「0-4」の「0」を、その「基準点」という意味として扱っていきましょうと。そうすると「0-4」というのは、「上の図とは逆向き（左向き）に4進め」というふうに捉えていこう、という話になります。

これで初めて方向が生まれるっていう感じですね。これでやっと「あ、-4って出てきたね」という。

そうやって捉えてあげると、ルールとしては意味がわかりやすくなる。⋯というのは、結構「みなさん自由に作っていい」っていうことなんですよね。

子どものおもちゃを想像するとわかるんですけど、レゴブロックを与えてあげて「家とか何か自由に作ってごらん」というのに結構近くて。自由に作らせてあげて、そうすると何か意味が立ち上がって。

そして、意味が立ち上がっても前のルールと矛盾とか差異がなければ、数学は結構許されてしまうというのがあるので。

いいよ

じゃあ、作ってしまった後は「元に戻るか確かめればいい」ということですね。-4に4を加えて0に戻るんだから「じゃこれはなんかこれで良さそうだ」みたいな、そんな話になります。

ということで何が出てきたのかというと、小学校からやっていた⋯小学校で「整数」っていう言葉、やりました？何ていう呼び方するんですかね、小学校って。

そうですね。「数字」って言うんですかね。本を読んでいたら3つの言葉が出てきたんです。

・「数」
・「数字」
・「数値」

「これらの言葉には違いがある。この違いは何でしょうか？」ということを書かれていて。「いやそんなの考えたことない、どういうことだ？」みたいに思いますよね。

「概念」というか、1というのは見えないものです。「1本」と言ってしまえばわかるけど、「じゃあ、1というのがどこかにあるんですか？」というと、「1そのもの」というのは、そこら辺を探したところで見えない、みたいな。

そういうことなので、「数」は「概念」みたいですね。だから、これは中学生でも高校生でもそうなんですけど、テストをすると⋯僕の場合は、期末テストの採点をしていると、答えの中に0が含まれると、0というのを排除する子が数名出てくるんですよね。

「0って”ない”んだから、0なんてものは無いんだから、答えにはならない」

という心理がはたらくみたいです。0というのは、無いものに対して記号を当ててるんだから「無いんだから書かなくてよくない？」という心理になるみたいです。

なんか、これがすごく不思議だなと思っていて。

だから0という概念=無いものに対して数字を当てているわけですから、ここで初めて1や0というものが出てきて、「数字と数値の違いは何なんだよ」みたいな話なんですけど、これは計算をした後の結果みたいな感じですね。足し算を計算した値、みたいな感じで出てくる。

だから数字を元にしたものが「数値」っていう、そういうイメージみたいですけど。

まぁ普段なかなか意識しないので、こういう違いまで気になっていくんだろうなっていうのは、たぶんこの「0」のせいかもしれないですね。

というのがあって、今回は、実はそのまま、以前みなさんと一緒にやった「自然数」という世界、そこから整数という世界に広げていく、ということをやったんですが、じゃあ今回は「もっと数の世界を広げていく」っていうことを一緒にやっていきます。

数の世界をさらに広げてみよう

「集合」っていうものがあるんですけど。言葉で書くとただの「集まり」なので、なんか「集合してください」みたいなものと思えばいいわけですけど。

数学の場合は「何か決まったものを集める」というものです。前回やったもので言うと「自然数」を集める。で、自然数を全部集めていったものを、袋の中に入れていくっていう発想をするとわかりやすいんですけど。

「自然数」は、英語では「natural number」って、そのままなんですね。自然な数だから⋯いや僕にとっては全然自然じゃないんですけど。

それで「ℕ」っていう記号があるわけなんですが、普通の「N」と違って、二重線を書くんですよね。ローマ字は普通「Natural」なんですが、記号っぽくしたいから線を入れて、1画目を二重にしたり、「ℕ」にしたりするっていう方法があって。

で、数学って、物の集まりをいくつか並べて「それがどんなふうな違いがあるか」を研究したりするんです。例えば、「偶数と奇数の違い」とかね。2で割ったときの余りとかをやるので、これは「時計」がわかりやすいですかね。

「13時=午後1時」ってありますけど、あれって、「13」を「12」で割ったときの余りを数えています。あれは12まで基準にすればいいので、まず自然数が出てきますね。そこで、自然数全体というのを次のように表します。

ℕ={1,2,3,4,⋯}

ℕ=のあとは中括弧で表して、1番小さいものから並べていくんです。「これが全部自然数だよ」っていうふうな書き方をします。

で、この後に整数がでてくるんです。整数は、実は英語の表記を記号として当てて無くて、ドイツ語の方を当てちゃってるんです。

整数は、英語の場合は「Integer」っていうんですけど、本当はこの「I」を当てていいんですけど、「Interval」=「区間」という別の記号の方で使われてしまっているものだから「I」は使わないで、ドイツ語の「チール」( Zahlen / GanzeZahl )の太字記号「ℤ」を当てるというのが決まっています。

これで自然数があって、1,2,3⋯とあって、これに0があって。

ℤ={　　0,1,2,3⋯

左には全部マイナスがいますっていう。

ℤ={-2,-1,0,1,2,3⋯}

これが一応、整数世界になります。

ここまでが前回なんですね。今日はこの上をやりたいっていうことです。

ℕの世界とℤの世界

ということで、これを何回も書くのは大変なので、わかりやすくまとめちゃいます。自然数のパネルと整数のパネルを使って考えてみると、多分わかりやすいと思うんです。

この自然数という世界があって、この上に整数の世界がいます。

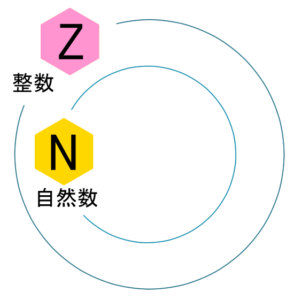
こんな感じです。

そうすると、ℕの枠の中に1,2,3⋯がいて、でℤの枠の中に0と、さらに-1,-2,-3⋯と。こんなのがいます。

前にお話した「0-4」とかっていうのが、つまり「小さいものから大きいものを引き算する」というのが小学校では出てこないのには、実はこれには理由があって。

もちろんマイナスを習っていないというのもそうなんですけれども、最初のこの「数の世界」の中で、何かを2つ取ってきた時に、その2つで足し算・引き算・掛け算・割り算のどれをしたとしても、この世界の中でちゃんと収まるものしかやらなかったんですね。

例えば、「4÷2」というのがあります。「4」と「2」というのは、自然数の世界の2つを取ってきました。

で、その中で割り算をしたときに、この結果って2ですから、結果もこの「ℕ=整数世界」の中にいるんですね。

ところが、これを逆にしてしまうと

2÷4=

この結果は何になります？

そう、1/2ってことですよね。ここの「ℕ=整数世界」の中にいないんですよね。「ℤ」の枠の中にもいないんですよね。ということは、今度はどういう世界が必要になるんでしょうかということになるんです。

こんなふうにして、みんなで世界をつくっちゃってるんですね。

結局、やりたいことって「足し算・引き算・掛け算・割り算」をやりたいんですけど、何でもかんでもこの「ℕ」と「ℤ」の世界から取ってきた中でこの結果が収まるかっていうと、そうではないっていうのが出てきちゃって。

だから、最初に出てきちゃったのが小さいものから大きいものは引けないっていうのは、この自然数の中に入ってないから。

で、それをもし、完全にどの計算結果をやったとしても、その中に入っていれば「足し算・引き算・掛け算・割り算」に関して「閉じている」っていう言い方をします。

つまり「小さいものから大きいものを引いたとき」っていうのは、引き算の中で自然数は「閉じてない」んですね。

だから、閉じさせたいんですね。

封じ込めたい感じです。封じ込めるために、1回、ℕの世界からℤの世界まで、世界をもっと広げたっていう。

そのために何が必要だったのかっていうと、「0」がどうしても必要になっちゃう、っていうことですね。マイナスを登場させるためには0がないと、何を基準として左側なのか、右側なのかがわからないんですよね。

これは、実はホテルとかにも影響を与えているんですね。日本のホテルって、「0階」ってないですね。西洋だと「ground floor」 みたいなのがありますね。あれがあるおかげで、「0階、1階、2階」っていう区別をちゃんとしています。ですから、他の国はちゃんと「0」っていう概念をめちゃくちゃ大切にしてるっていうのが、すごく表れていますね。

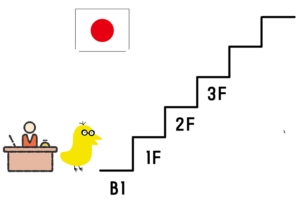
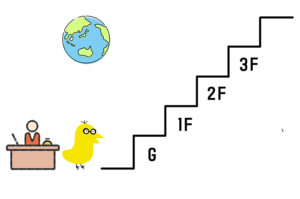
なので、「基準」というのは結局大事になります、っていうことで。

そうすると「地下1階」っていうのが、なんかあんまり…「1F」とか「B1」とか見たとしても「B1って結局なんなんだろう？」っていうふうに残っちゃうんですけど。「地下1階」って、何に対する「1階」なのか？っていう。

そこがわかってくると、世の中大体、数字転がっちゃってるんですよねっていうのはあります。

ということで、この整数の世界に広げたのは、引き算をまずその世界で「閉じさせたい」っていうのがあって。

「足し算」は全部大丈夫です。必ずこの「ℕ」中に閉じちゃうから大丈夫なんですけど、引き算がまず問題で。

で、そうすると結局人間は何をやりたくなるかっていうと、掛け算でも閉じさせたいし、割り算でも閉じさせたいんです。でも、割り算は閉じさせてくれないんです。4÷2はいけますけど、2÷4がいけないんですね。2÷4が1/2になっちゃうから。

ってことは、この自然数・整数の外側って、どんな世界が必要になりそうですか？どうでしょうか。これ、小学校6年生くらいで出てくる分数が必要になるってことですね。

「なんで分数をやってるんだろう」みたいな話が出てきて「分数を分数で割る」なんて話が出てきたんですけど。「分数を分数で割る」って、その中で完成させて、閉じさせたいんです。計算結果を「5/6÷12/7は？」とか聞かれても、意味がわからないですよね。だって「何を言ってんの？こんなの日常生活でいつ使うんだ？」みたい話なんですけど。

あれはもう計算結果をその中に納めさせたいための、新しい、拡張させたことなんですけど、この世界が今度は⋯まあ分数って言ってもいいんですけど、数学はもうちょっと正確に「有理数」というふうな言葉を使います。

有理数も、西洋から言葉が入ってきたときに結構誤訳なんじゃないかと思うんですけど、「比」で表せるんだったら「有比数」って書けばよかったんじゃないの？みたいなふうに言われるんです。

これ元々、英語だと「rational number」＝「合理的な数」っていう。何が合理的なのかよくわからないんですけど、「合理的な数」っていうのの直訳を、多分当てちゃってるというのがあって。

昔の人が、最初に偉い人が訳を当てちゃうとこうやって残っちゃうんですよね。だから「有理数」って聞いても何かみんなピンとこない、っていうのはしょうがないんですよ。昔の人が決めちゃったものが残るので。

とりあえず「有理数」というのが「分数」ということなので、分数は割り算が入ってきちゃうから、「商」の話をするんですね。割った時の答えのことを「商」と言いますが、英語で言うと「quotient」というんですね。これも頭文字の「Q」を取って太字二重線にして、こうやって新しい世界を広げるっていう感じです。

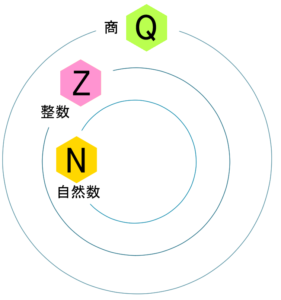
そうすると、今度は割り算の世界も完全に収まります。何でもいいので、何か好きな割り算を言ってください。

(笑)。じゃあ何でもいいので好きな数字を2つ言ってみてください。それを割り算してみましょう。プラスでもマイナスでも何でもいいです。

マイナスの数も、何か言ってみてください。

そうするとこうなりますね。

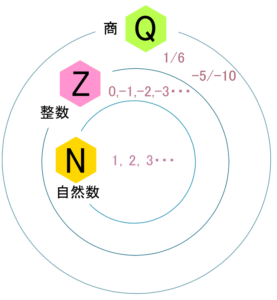
今回はマイナスとマイナスが「掛け算の場合はプラスになる」とやったので、割り算も同じようにプラスになりますので、1/2という形で、結局こういうふうに書けます。

これで割り算ができるようになりました。嬉しいですね。ということで掛け算もできるようになって嬉しいですね、みたいになってくるんですね。

「何が嬉しいの？」と思われるかもしれないですけど、計算できる世界が広がっていくのが一番嬉しい。というのは、何かこう、自由になっていくんですよね。

子どもたちのことを想像してみたらわかるんですけど、なんか縛られてる中で遊ぶ⋯例えば「砂場の中だけで遊びなさい」って言われるのと、「外も使っていいよ」って言われるのとでは、行動範囲が増えるっていうか。

そうするとなんか面白くなるよねっていう。そういう話が出てきます。

だから実は、ここら辺で「数の世界、もうよくない？」ってなってきませんか？(笑)　自然数、整数、有理数…って言ってて、もうお腹いっぱいって感じしますよね。

〈後半へ続きます！〉

 

動画をご覧になりたい方はこちら↓