こんにちは。究進塾編集部です。

究進塾youtubeチャンネル「新井先生の数学史」第1回の続きです。前回は、歴史上の数学者もマイナスの数を受け入れられなかったということがわかりました。今回はいよいよマイナスの数を受け入れ、「量の概念を手放す」ということについての解説です。

講師：新井康仁
日本大学文理学部数学科卒業 東京理科大学理学専攻科数学専攻修了

新井康仁

あるときは「分数の割り算」や「－×－＝＋」といった当たり前の概念を受け入れられない生徒に向けて、「実は数学者もそうだったんだよ！」と共感し、数学史を紐解きながら、数学者がどのように考えて、受け入れたか、を説き、またあるときは、数学の漫画や絵本を薦めて、生徒の数学への好奇心を掻き立てることに腐心する。「数学とは、すなわち考えること」を体現し続ける伝道師です。

前回の記事
【新井先生の数学史】第1回 負の数を理解するまでの苦闘

生きていると動くってことが先に出てきて、意味は後からついてくることもあるし、実はよく分からなくなってからが面白くなるっていうのが数学なんですね。今までと違うものが出てきたときに、「ちょっと待ってあげよう」「別に間違ったっていいじゃん」というか。

マイナスを受け入れられない数学者がもう1人。

哲学者の中で「デカルト」っていう人がいるんですけど。

デカルト（René Descartes） ［1596～1650］ フランスの哲学者・数学者。近世哲学の父とされる。方法的懐疑によってすべてを疑うが、疑っている自己の存在を真理と認め、「我思う、故に我あり」の命題によって哲学の第一原理を確立。さらに、この思惟する実体と延長を本質とする物体を、相互に独立とする物心二元論を展開した。また、解析幾何学の創始者でもある。著「方法序説」「省察」「哲学原理」など。 （デジタル大辞泉 「デカルト」より引用）

「我想う、ゆえに我あり」っていう言葉、多分皆さんはもしかしたら倫理か何かの授業で習ったかもしれませんが、この人は今で言う「座標」の原型を考案したって言われている人なんですけど、あの人でさえもマイナスの数を受け入れられなかったっていう時期がありまして。

その後にまた新しい数が登場しても「こんなの存在しない」っていうことで、「そんなの偽りの数だ」っていう考えを当ててしまう時期がありました。

0ゼロの概念

ところが、今の話は全部フランスとかヨーロッパの「数学の時代」の話をしているんですが、実は「0ゼロの概念」って聞いてピンとくる国が、多分あると思うんですけど、どこの国でしょう？

そう！インドなんですね。実は、インドは結構早くマイナスの数を受け入れちゃってます。

マイナスの受け入れ方

記録に残ってるのが、7世紀のブラフマグプタっていう数学者が、書物の中で「借金を計算するときの計算」としてマイナスの計算を残しています。

ブラフマグプタ（Brahmagupta） [生没年：598-665以後] インドの天文学者，数学者。628年にラージャスターナのビッラマーラで完成した《ブラーフマスプタ・シッダーンタ（梵天により啓示された正しい天文学）》はブラーフマ学派を代表する天文学書として，インドはもとよりイスラムの天文学にも大きな影響を与えた。同書には数学に関する2章が含まれていて，とくに不定方程式や図形の問題には数学者としてのすぐれた才能が発揮されている。若いときに書かれたこの書物では先人の業績を厳しく批判しているが，晩年に著した天文計算書《カンダカードヤカ》においては，アールヤバタの学派を継承・発展させている。この書もインド内外においてきわめてよく利用された。 （改訂新版　世界大百科事典 「ブラフマグプタ」より引用）

皆さんが意味として分かりやすいのは借金の例だと思うんです。借金の例だと、この「0-4」の答えが「-4」だっていうふうに受け入れるのは簡単なんですよね。

だからさっきの規則を大事にした上で「0-4」っていうのをとらえると、最後は「0+4」で「0に戻ってほしい」ということがイメージできると思います。

逆の計算をしてるから「戻ってほしい」という話になっちゃうので、歴史的にはこの後「数直線」っていうのが必要になります。

そうすると、実は「量」の概念から抜け出さなくてはいけなくなってしまって、じゃあどこに行くのかというと、今度は「位置」の話になります。

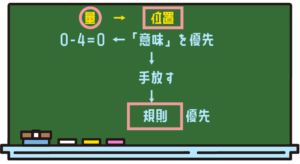
数直線を思い出そう！

数直線って、覚えてますか？

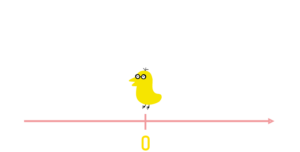
こういうやつです。0は「原点」です。

0-4っていうのが最終的に-4になるっていうことをどうやって受け止めたのかっていうのは、これは中学校の教科書の一番最初で、人間が動く例が載っていると思います。原点に人がいるとして、右を「東」、「西」を左、みたいにしてあげるっていう感じですね。

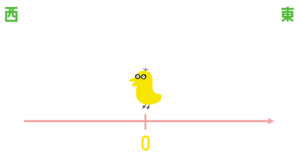
そうすると、最初に0っていうところにいたときに、じゃあ「-4」っていうのを、捉え方としては・・・今「位置」っていう話をしましたけど、この図を見ると今どうやって捉えられますか？

そうですね、これは「進む」っていう感覚ですかね。「どっちに」っていうのを、符号で方向づけをしているような感じですかね。プラスだったら東方向、西に行きたかったらマイナス方向、みたいなふうに決めているので、-1、-2、-3、-4・・・みたいな感じで方向づけして動く、っていう感じになっています。

でもこれだと、つまり「-1と-1をかけると1になる」だと、多分この移動するっていうのが伝えられないとは思います。では、-1×-1の前に、

1×（-1）=

これだったらどうでしょう？

そう、(-1)が「西」を示していて、1が「1個分進む」ことを示していますね。だから、始まりは「1×（-1）= -1」というところから始まったんですよね。そうすると困るのが

-1 × -1 =

の話です。それで、さっきの「1 ×（-1）」の方の話ですが「1に対して(-1)かけると答えが-1」というのを「もう1個の捉え方をしてみましょう」というのが、今回のお話になります。

1×(-1)=1 の捉え方

最初の「1」というのを、数直線上の「1の点」だと思ってもらうんですね。で、最後の「-1」っていうものを、数直線上の「-1」と捉えます。この「1」の点と「-1」の点を、「×(-1)」がどう繋げているのか、というふうに考えるんです。

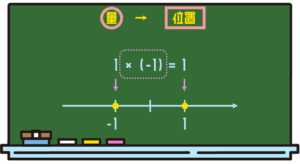
「×(-1)」にどんな意味を持たせたら、みんなの解釈がもうちょっとすっきりするだろうか、みたいな。ということで出てきたのが、今度は「回転」という方法なんですね。

回転とは？

「× -1をする」っていうのは「原点を基準にして元の点を180度回転させたらどうなりますか？」と捉えるという考え方です。この例の場合だと、原点を中心に回転させると、1の点が-1の点のところにきますね。

この方法で、式の数字を別の数字に変えてみましょう。最初の1を「2」に変更してみます。式は「2×(-1)=」ということで、数直線上に「2」っていう点があって、それに(-1)をかけるっていうのは、かけた後に180度回転するから・・・っていうふうに、頭の中でイメージができるわけですね。

なので、「反対側にとんでいく」っていう感じですかね。

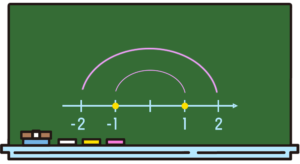
「×(-1)」っていうのが、「180度回転」っていうふうな、図形的な認識を持てるようになるっていう感じですね。

いよいよ-1×-1を考えてみよう！

で、最初の質問がまさに、この「× (-1) を2回行っている」っていうことなんですね。だから(-1)と(-1)っていうのを考えるときに、元を基準にしてもいいですね。「1」っていうやつが最初にいたとして、「1 × (-1) × (-1) =」とやってもいいんですが、しなくてもいいので「“180度を2回転してる”って捉えてもいいよね」っていうことです。もしくは、「-1をスタートの点にしちゃう」っていう。-1の点から始まったとして、ここから180度回転させるって考えることができます。

こうすると「-1 × -1 って、こんなことをしてるんだろうな」っていうニュアンスというか、“感じ”ということですかね、なんとなく掴めると思います。

「動く」が先か、「意味」が先か

生きていると「動く」っていうことが先に出てきて「意味」は後からついてくることもあるし、先に「意味」がわかって後で「動く」っていうこともあるし。数学をやっているとそういうことを考えちゃうっていうのがあるんですけど。「動く」っていうことと、「感じる」っていうことですね。

動く ←→ 感じる

意味を先に捉えようとしちゃうと、先に「感じる」っていうことを捉えようとしちゃうっていう。だけど数学は、「先に動いてしまう」っていうのが数学の存在なので、「もう先に動いちゃうんだよね」っていう。で、動いた結果「何をやっているんだろうな」っていうのを観察していくと、結構感じられるというか。分数を分数で割っていかないと「あれっ分数を分数で割るってどういうことか？」みたいなのが感じられない、みたいな。そういうことに近いのかもですけれど。

それを今、「感じていく」っていうことをやってるんですね。

だから勉強の勉強の仕方で、結構「計算が面白くないな」っていう時が来ると思うんです。学年が上がるにつれて、抽象的になっていって「なんか言ってることがよくわからない」ってなるんですけど、実は「よく解らなくなってからが面白くなる」っていうのが、数学なんですね。「よく解らなくなってからが面白い」というのは、解らないときって「感じられない」から、「感じるってどういうことか」みたいなのを探すというか。

その「どういう感じ」っていうのは、例えると球技でサッカーやバレーボールがあると思うんですけど、その「ボールの振る舞い」に近くて。例えばバレーボールだとレシーブするわけですが、最初うまくいかないわけですけど、「ボールがこういうふうに返ってきたときには、ここに当てればいいんだ」みたいなのって、それにだんだん近づいていって馴染んでいって、体で感じていくっていうか。

それで後で意味が解って「あ、だからこの練習はこのためにやってたんだ」っていうか。意味は後についていってるような気がするんですけど。

練習のメニューは「こういうメニューだからやってますよ」っていうふうに先生に言われて「じゃあこういうメニューだからやるのか」みたいな。そういう感じだと思うんですけど、プレイヤー自体は、やってるときは多分最初から意味が解ってないと思うんですよね。「言われたからとりあえずそうなんだな」っていう感じでやっているというか。それにすごく近いと思うんです。

そう考えると、なんか「数学も部活動もそんなに変わらない」というか。「勉強」っていう名前がついちゃってるから変わって感じるということがあるかもしれません。

そういう今までと違うものが出てきたときに「ちょっと待ってあげよう」というか。「振る舞いをちょっとずつ見ていくと、何か見えてくる」みたいなふうに構えておくと、嫌になる確率はちょっと減っていくというか。そういう受け入れというのが必要かなと思っていて。

高校生とかであれば、留学生が来たりすると思うんですけど、留学生が来た時に、英語が話せないから「ちょっと不安だな」というか「緊張するな」というか、「うまく話せなかったら伝えられない」っていうふうに思うかもしれない。そういうことにちょっと近いなと思っていて。なんかよくわからない数が出てきたからこわいなというか。「これ、できなかったらどうしよう」というか。

新しいものが出てきたときに、ちょっと広く構えてあげて「別に間違ったっていいじゃん」というか、そういう感じで掴まえてあげるといいのかなと思っています。

今回のまとめ

第1回目は「マイナスの数」の話をメインにしました。次回は、中学校3年生で学ぶ「√（ルート）」あたりの話が出てくるんですけど、実はこれもみなさんと多分一緒だと思うんですけど、とある有名な数学者が「√2」っていう数を受け入れないために、いろいろな問題が出てきます。

ということで次回は「無理数」のお話をしていきます。

お楽しみに！

今回の動画はこちら↓