こんにちは。究進塾編集部です。今日は新井先生の数学史「第3回-後編」をお届けします。前回の内容では、虚数が登場した背景を追いかけてきました。

今回は、発見してしまった虚数を、数学の天才たちはどう捉え、受け入れていったのかについて解説していきます。

前回の記事
【新井先生の数学史】第1回-前編 負の数を理解するまでの苦闘
【新井先生の数学史】第1回-後編 量の概念を手放した先とは？
【数学史第2回-前編-】四則計算のすべてで閉じる世界の創造
【数学史第2回-後編-】無理数の発見による最悪の結末
【数学史第3回-前編-】虚数が初めて登場する歴史的な背景
【数学史第3回-後編-】虚数の居場所を見出すまでの歴史的な背景

前回・今回の内容

前回お話しした内容の最後に、カルダノっていう人が出てきました。前回話した内容、何か覚えていることあります？

いろんな数の話をしましたね。

そう。無理数に始まって、無理数と有利数が合わさって、なんていう数になりましたっけ？ヒントは、英語だと「Real number」っていいますね。

はい。実数がまず出てきて、その上に虚数って数が出てきます。虚数って「Imaginary number」って当ててますけど、これはデカルトが名前をつけているわけなんです。デカルトが結構、重要な人物としてあげられます。

2次方程式の歴史が長いので「方程式って、暗黒の時代が結構続きました」みたいな、そんな話をしていきます。

2次方程式に至る前

2次方程式が出てきたのはピタゴラスとかの辺りなので紀元前の5世紀とか4世紀とかそこら辺なんですけど、実はもっと前に2次方程式を計算しているのが残っています。

それが紀元前の4,000年とか、それ以降の古代エジプトとかです。皆さんも世界史で「ナイル川の近くで文明が栄えましたね」とかっていう話をやったと思います。

ナイル川って毎年8月から10月ぐらいで必ず氾濫が起こる時期があって、それで自分たちの土地が流されてしまうから、どうしても「測量」=土地の面積を図るっていうことが必要になったところから始まってるんです。

古代エジプトの他に、もう1つ世界史でよく出てくる、メソポタミア文明でも同じようなことがありました。「川と川の間」という意味がある「メソポタミア」は、チグリス川とユーフラテス川の間で栄え、紀元前3,500年から539年ぐらいの文明がありました。

紀元前4,000年って、全然イメージできないところだと思うんですけど、このくらいからもう2次方程式をやっているっていう感じです。

ここら辺は「ユークリッド」っていう人、これは世界史では「エウクレイデス」っていう名前で出てくるかなと思うんですけど「ユークリッド」っていうのはこれの英語読みですね。ギリシャ語だとエウクレイデスって書きます。多分、世界史の資料集とかに載っています。「ユークリッドの原論」っていうのが載ってたりするんです。

この「ユークリッドの原論」って、当時「聖書に次ぐベストセラー」って言われてます。それぐらいものすごく長く読まれている本なんですね。ニュートンとかも、この人の本を読んで勉強したらしいんですけど、そういう人がまず出てきます。

その後、ディオファントスっていう人が出てきます。おそらく「フェルマーの最終定理」っていうのは皆さん聞いたことあるかもしれないんですけど、フェルマーがディオファントスの算術をアレンジしたんです。このディオファントスが書いた本に書き込みを入れていきながら、自分で問題をアレンジしていって出来上がったのが「フェルマーの最終定理」っていう。なのでその元を作った人です。ディオファントスはギリシャの人なんですけど、エジプトに遠征しながらそういうことをしました。

高校生で習う、この人に関するものだと、整数の性質の時に「不定方程式」っていうのが出てきます。方程式の数と未知数の個数がずれるっていう、「\(ax+by=c\)でここの\(a\)と\(b\)を求めなさい」みたいな、そういうのやると思うんですけど、「ディオファントス方程式」と言われることがあります。

で、この人たちの時代でも、まだ2次方程式の解の公式はまだなんですね。

みなさんは中学校3年生で習いますけど、解の公式って覚えてます？

解の公式っていうのは、

\(ax^2+bx+c=0\)
\(x=\)

という、「\(a\)と\(b\)と\(c\)で表しなさい」みたいな。そういうことをやっています。これは後で図形から作っていきますので、数学的な解説はここでは省きます。

このように、この部分に至るまでにかなり時間がかかっているっていう話を今からしていきます。

まだまだ時間がかかる数学の進化

全然まだ、進んでいないんです。方程式自体は「言葉で説明されて書いていく」という方法です。

その後にブラマグプタっていう人が出てきます。ブラマグプタっていうのは、教科書でいうと三角比のところに関係する人です。「ヘロンの公式」っていうのをやると思うんですけど、あれはこの人から来ています。

ヘロンの公式は三角形の面積の公式です。

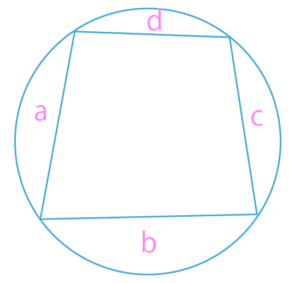
上に、円に内接している四角形ABCDがありますね。で、大文字のSと小文字のsの2つが出てくるんですけど、

\(s=\frac{a+b+c+d}{2}\)
\(S=\sqrt{(s-a)(s-b)(s-c)(s-d)}\)

こういう公式がありますが、この式のdの部分を0に近付けると、図形の四角のdの長さがちっちゃくなっていって、三角形になります。

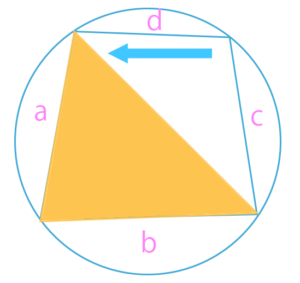
ヘロンの公式を学校の先生は推奨してないっていうのがあります。ルートの中にルートが入ってくると、二重根号がめんどくさいので、あんまりお勧めはしてないんです。けど、検算で使う分にはいいよねっていうところで出てきます。なるべく公式をたくさん教えないようにしてるのは、「覚えなきゃいけない」っていうふうに思わせたくないっていうのもあるのであんまり教えないんです。でも余裕があったら…というかここら辺だと完全に趣味の領域に達しちゃうので。

この辺りがブラマグプタのところなんですけど「流石インドだな！」という感じですね。この辺りになると、もう0も受け入れてるし、マイナスも受け入れています。大体5世紀ぐらいで0とかマイナスっていうのも出てくるんですけど、この人が書いた数理天文書の中に、初めて「借金の計算」とかでマイナスの計算が出てきます。

マイナスの計算をヨーロッパが受け入れるのはもっと後です。全然後です。パスカルの話をした時に言いましたが、パスカルなんか「0-4」さえ受け入れないですから。17世紀でですよ？17世紀ってことは、ブラマグプタから1,000年後です。1,000年以上かかるっていうのは、何か宗教的なものが邪魔してるような気はしますけど。そこら辺はインドは早めにすんなり受け入れてるような気はしますね。ヨーロッパでは、ピタゴラスの時にも無理数を受けれなかった文化とかがありますので。新しい数が出てくると、みんななかなか友達にはなりたくないみたいな、そういうのがあるかなという感じです。

そこら辺が、インドであったことです。

しかしまだ7世紀だった…

ブラマグプタでさえ7世紀なので、ここから1,000年でようやくパスカルです。「1,000年、何してたんでしょうね？」っていう。他の国は何をやってたんだろうみたいに思ってしまいますよね。パスカルはフランスですけど。

ヨーロッパどうしたんだろうね…っていうところで、1,200年代にフィボナッチっていう人が出てきます。

フィボナッチ数列っていうすごく有名な数列がありまして、お父さんが貿易商人だったってこともあってアラビアとかを経由して、ヨーロッパに「算用数字(今一般的に私たちが使っている0,1,2,3,4,5,6,7,8,9の表記)」を持って帰りました。ローマ数字の「Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ,Ⅵ,Ⅶ,Ⅷ,Ⅸ」っていうスタイル、ちょっと不便だよねっていうのを改めて、それで今度はヨーロッパが栄えるという話になっていきます。これはフランスのお話です。

そして今度はビエトっていう人が出てくるんですが、この人は数学者っていうよりは、法律家なんですね。

フェルマーも一緒で、弁護士というか裁判官というか。そういう職業の人たちが暇を持てあまして数学やってた時代ですね。「暇だったら数学やるんですかね？」っていうツッコミを入れたくなりますけど。

それはそうとして、ビエトはフランスの法律家・数学者ってことで、王様のアンリ4世に仕えていたっていう人です。この人がやったことが結構大きくて。

今皆さんが使用する教科書に載っている、さっきも書きました「\(ax^2+bx+c=0\)」っていうのは、今はこうやって方程式として「これ一般的な式だよ」っていうふうに教わるんですけど、数学が嫌な人って、これ全部文字列に見えちゃうんですよね。「\(ax^2+bx+c =0\)…全部分かんないじゃん…」みたいな話に見えてしまいます。

よく、数学は「文字は何でも置いていいよ」っていう言い方をするんですけど、何でもいいっていうふうには言ってるものの、言ってる側は「何でもいいとも思ってない」っていう。

「じゃどう思ってんだよ」って話なんですけど、そこでデカルトを紹介します。

現代にもつながるデカルトの発想

ビエトとちょっと比較をしてみましょう。

ビエトの実績は何だったのかって言うと、今で言うと分からないもの=「未知数」は\(x\)とか\(y\)とか\(z\)みたいにアルファベットの後ろの文字を使うっていう文化がありますが、これはデカルトの影響なんです。

そして\(a\)、\(b\)、\(c\)みたいなアルファベットの最初の文字を使うものは、これは「既知数」って言って、ただの定数というふうな1とか2とか3とかみたいなものですよっていうふうな見方を実はしてるんですね。

だから、数式に色をつけてるような感覚なんですよ。そういうふうに思ってもらえると、数式の読み方が変わります。ただの文字列のような感じはしなくなるので、高校の数学で「因数分解しなさい。〇〇という文字について解きなさい」って言われた時に、それに対して「意味が分からない！」みたいになるっていうのは、多分この変数と定数っていうのがよくわからないっていうふうになってるのかなっていう感じですね。

ビエトがデカルトに影響を与えたことは何かっていうと、元々ビエトは既知数を母音で、未知数を子音で表すとかっていうのをしているんですね。でも、母音とか子音とかで表すのだと、ちょっと難しくなっちゃうんです。

デカルトの方が今の皆さんの教科書に近いところは、「求めたいものを\(x\)で置きなさい」ってよく言われるのは「分からないものを\(x\)と置くんだな」っていうふうに見ています。これが、教科書がデカルトさんの影響をもろに受けてる部分じゃないかなっていうふうに思います。

そういうふうに思ってもらえると、デカルトさんに親近感が湧いてくるかなという感じです。

あとデカルトさんがやったのは、この人は結構色々な影響を与えちゃってて。古代のギリシャでやっている数に対する見方を大きく変えてしまったっていうのがあるんですね。

っていうのは、例えば\(a\)っていうものが「1つの量」っていうふうに捉えてた時代なので、例えば\(a^2\)ってなった場合、捉え方が今とちょっと違うんですけど、\(a\)は1つの線分で見てるんですね。だから1個の長さとして捉えてて、これを2乗した結果っていうのは、これは線分と線分をかけてるので面積って捉えてるんですよね。

今で言うと「\(cm^2\)（平方センチメートル）」って\(cm\)の上に2乗を書きますよね。これはそれを受け継いじゃってるから「量」から逃れられないんですね。逃れられないから、マイナスをどうしたって受け入れられないんですよね。デカルトさんはそれをぶっ壊してるのです。

量で捉えるということをやっちゃうと、\(a^4\)とか、絶対受け入れるの無理ですよね。4次元なので、まず想像できないよねっていうことになりますよね。

こういった「狭い見方」っていうのが、古代ギリシャからもっと前の時代になっています。

思考をもっと自由にさせてくれているっていうのが、デカルトがやったこととして1番大きい。完結にまとめちゃうと、次元の枠を取り去っているっていうのが大きいですね。

結局\(a\)だって1次元、\(a^2\)は2次元＝平面で考えていて、で次は\(a^3\)にすると体積になるので、これは立法体の体積を求めるみたいなやつで、「縦、横、高さが出てくるから3乗なんでしょ」とかっていうのが出てくるんですけど。

\(a\)→1つの線分
\(a^2\)→面積
\(a^3\)→体積

これだと限界があるよねっていうところです。

これらは全部「1つの量」と捉えてしまおうっていうふうに発想します。キリスト教とかの文化をそのままずっと受け継いでいる時なんてのは、\(a, b, c\)の未知数とか既知数、こういった文字を数字扱いしてるので、そういう時は「絶対にこれはマイナスを取らない」っていう見方をしちゃってるんですね。

だからマイナスの数が出てきた時には「もう意味がない」みたいな判断をしてしまいます。意味がないと先に進めないですから、どうしたって遅れますよねっていう。

「新しい発想」をできることがすごい

あとは僕が高校生の時にデカルトに共感できたところがあって。

デカルトも、古代ギリシャの図形「ユークリッドの原論」を読んでいたんですけど。ここに書かれてるものって、ほとんどが図形の証明…というか図形に対する考察が主に書かれているので、読むのがすごく大変なんです。「〇〇ならば□□である」というように内容が全部証明なので今読んでも大変で、すごく無機質的な扱い、論理だけをすごく大切にされてしまってるんです。なので想像力が必要で。図形に対する想像力も必要になってしまうし、例えば補助線を引くとなったら感覚も必要になったりするし。

常に図形に限定されている世界っていうのはすごく息苦しいというか。「もっと自由にさせたらいいんじゃないの？」っていうふうに、デカルトさんはずっと思っている。

だから実はこの面倒くさがりな側面が、自由度を上げようとするところに繋がったという感じなんですね。この次元を全部取り去ってしまって「1個の量」「1個のもの」として、数字として考えればいい。

それがなかなかできないですよね。新しい発想っていうのが。だから、今までの発想を1回白紙にして「じゃあ、こうだったらどういう世界が見えるだろうか」って考えるのは、現代に生きていても大事になるような考え方かなって感じます。

それで出てきたのが図形の分野と、デカルトがやっていた代数（文字を1個の数字として扱う）分野です。「代入」っていう言葉は、このあたりの人たちがいないと出てこないんですよね。

今は当たり前のように\(x=2\)を代入するっていうことをやってますけど、アレ全然当たり前じゃないんですね。「文字に数字を入れるなんて、おかしくない？文字と数字は違うだろう」って思ってしまう。だけど、数学でよくあるのが「同一視」っていうのが出てくるんですよね。「違うものを同じものと見る」っていうのはすごく出てきてしまいます。

数学に抵抗感がある人は「\(x\)の中に\(x+2\)を代入してください」って言われると、意味わかんなくなるんです。「どういう…？何を言ってんの？」って。1つの塊の中に塊りを放り込むっていうのが、なかなか抵抗感があるから。

だから「関数が嫌になる」っていうのはこういう要因があるのかなっていうふうにすごく感じます。これ本当は「すごく便利なものが出てきた！」っていうことなんですが、それが二極化してしまっているのかなと感じますし、「便利さ」を逆に「難しさ」と捉えてしまうというのも同時に出てきちゃってるんです。

これについての対策は、いきなり問題を解いて慣れていくよりも「どうして便利なのか」みたいな、そういうところを知ることが近道なんじゃないかなと思います。この人たちの考え方が出てくる前の不便さを1回味わって「じゃあどうして便利なのか」っていうのを味わっちゃった方が、多分抵抗感はちょっとずつなくなるんじゃないかなっていうふうに思ってますね。

\(x, y, z\)とかにちゃんと意味付けをするというか。実際はいいんですよ別に。\(a, b, c\)は既知数、\(x, y, z\)は未知数だって、数学者たちは思っているし、数学の本を書いてる人たちはそう認識をしてるから問題文で「\(a, b, c\)は定数とする」って書いてますよね。

実際は「〇〇と置く」っていう宣言をしてもらえればどっちで使ってもらってもいいと思いますが、皆さんは多分もうデカルトの\(x, y, z\)に慣れ親しみすぎちゃってるので、「\(x, y, z\)を定数とする」って書かれてしまうと、逆に気持ち悪くなるんじゃないかなというふうに思います。

「2次方程式の解の公式」を図形で考えてみよう

2次方程式の解の公式に辿り着くまでに1,000年かかったんですが、それを順に追って一緒に見ていきたいと思います。最初は量の話をして、そこから代数の世界に行くっていうのを、図形のところから一緒にやっていきましょう。

簡単なやつにしますね。

いきなり\(ax^2+bx+c=0\)をやるの難しいと思うので、ここは最終的なゴールとします。この解の公式に到達することを目指します。

【目標の形】	【考えてみよう】
\(ax^2+bx^+c=0\)	\(x^2+2x=15\)
↓
\(x=\)

これをやるのはおそらく中学校の3年生ぐらい、公立学校だと中3、中高一貫校だと多分中2ぐらいでやります。この式を現代で解くってなった場合、右側の式を見てみると、右辺に「15」が残ってるので「なんか気持ち悪い」っていう感覚を持ってるんじゃないですか？「解の公式の方は右辺に0って書きましたよね？なんで右の式は右辺に15って書いたんですか？」…って思ったら、これは完全に、みんなはデカルトの影響を受けちゃっています。

なのであえて書いたこの15を見て、皆さんには「この右の式をどう読み取って欲しいんだろうな…」っていうのを感じて欲しいんです。

デカルトさんが出てくる以前は「量」で考えてたので、これ自体を「面積」っていう捉え方をしてるんですよね。なので図形をちょっと見てみましょう。

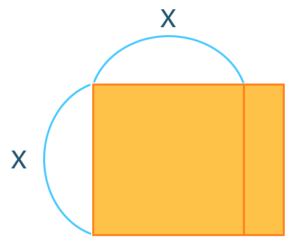
一辺が\(x\)の正方形っていう捉え方をして、\(x^2\)っていう部分と\(2x\)の部分を分けて見ていくことにします。\(x^2\)の部分の面積と、\(2x\)の部分の面積、と捉えます。

多分これ見てる人は「こんなことしなくても15を移行させて因数分解しろ！」って思ってるかもしれないですけど、ちょっと平方完成の話をするために簡単な例を見せてるだけなので、とりあえずこれで説明していきます。

そうすると、ここで縦×横で面積が分かりますよね。「\(x^2\)」と出ます。

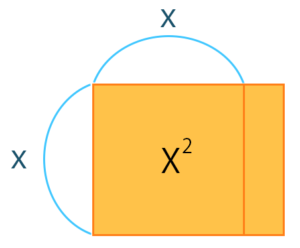
で、式にある「\(2x\)」っていうのは、図形で言うと次のようになります。

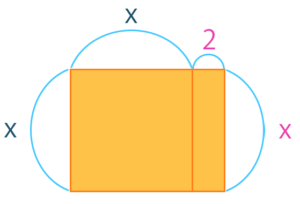
縦が\(x\)で、2っていうのが掛け算されてるので横の部分を2というふうに見てあげればいいよねっていうことです。

なのでこう考えると、\(x^2\)は正方形で\(2x\)は長方形なので、結局\(x ^2+2x\)までで長方形の面積なんですね。だから\(x^2+2x=15\)を考えるときには「“面積が15”って言ってる」って思ってもらえればいいです。

昔の人が解けなかった問題は、右辺にマイナスがあるとき。面積がマイナスになっちゃうから「そんなの受け入れない」っていう時代だったんです。だからこういう方程式ばっかり解いてたんですよね。マイナスを受け入れてないから、それでどうしても先に進めないんですよ。

さて、話を進めていきます。

今、高校生で2次関数のグラフをやる時に「平方完成」っていう言葉が出てきます。「平方」って何のことでしたっけ？

\(cm^2\)、これです。2乗のことですね。なので「2乗を作りたい」っていうのがあるんですよね。

【目標の形】	【考えてみよう】
\(ax^2+bx^+c=0\)	\(x^2+2x=15\)
↓ 2乗＝平方完成
\(x=\)

で、今これ長方形なので2乗にならないんですね。なので「縦と横を揃える」っていう発想をします。これを正方形の面積にしていこうっていう。

そのために何をしたかって言うと、平方完成をした経験がある人は分かると思いますが、\(x^2\)の係数aで割ってあげて2で割る…とかっていう作業が出てくるんですけど、2で割るっていう作業をさっきの長方形で見ていくと、

この「2」の長さのところを、半分だけ移動させちゃうんです。

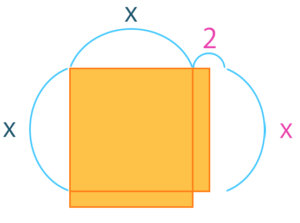
こうやって、長さ2だったところを長さ1にして、追加した部分も長さ1です。で、そうすると隙間が出てきちゃいますので、あとこの右下の欠けた部分があれば正方形になってくれますよね。

ここの欠けている部分の面積は、縦が1、横1が1の四角形の面積を、式の両辺に足してあげるっていうことをします。

\(x^2+2x+1=15+1\)

この式だけ見ていると図形の方が想像できなくなっちゃいますが、「元々の正方形の面積」＋「横1の長方形の面積」に、欠けた「1×1の面積」を足してるよ、っていう見方をすればよくて。

式を分けて考えてあげると「\(x^2+2x\)の面積と\(+1\)の面積は、結局正方形になる」ということです。

縦が\(x+1\)
横が\(x+1\)

なので、縦×横は何になりますか？

縦が\((x+1)\)ですよね。横も同じなので2回掛けるということは\({(x+1)}^2\)になって、右辺は16になります。

\({(x+1)}^2=16\)

2乗したら16になるっていうことで、これを「平方完成」って呼んでいるんですね。

数字でやると簡単なんですけど全部文字なので、いかに難しいことをやっているかというのが分かるかなと思います。この後は平方根を外して、\(x\)を移行してあげれば数字が出てきます。

\({(x+1)}^2=16\)
\(x+1=\pm4\)
\(x=3, -5\)

今、高校では実はこんなことしないんですけど。高校では「15を移行させて()にまとめて因数分解して解けば、答えが出る」っていう発想をします。

これ、右辺が15じゃなくてもいいようにするために、他の数でやってもらえるといいと思うんです。

例えば、\(x^2+2x=15\)の右辺を14に変えて\(x^2+2x=14\)とすると、正方形にした時に15になって、さらに計算していくと\(\pm \sqrt{15}\)になるので「√が結局必要になるよね」とかっていうことも分かります。

数字でやってみよう

ということで図形を思い出して、もう1回平方完成を数字に戻ってやってみるっていうのをやります。

図形から数式に行くときに、\(x\)の係数2で\({(x+1)}^2\)を割ってるんですよね。この場合はどっちも1を足したんですけれど、今だとこの\(x+1\)は中学校の3年生で「展開の公式」を習います。

\({(□+△)}^2=□^2+2□△+△^2\)

こういったものですね。これ中学校でやりますが「発想を変えて\(□^2+2□△\)を左辺に持っていくっていうのを考えると()の2乗をつくれるから、\(△^2\)をこっち持っていってあげればなんか作れそうだよね」みたいなものをさっきの\(x^2+2x=14\)の式に使っていく平方完成ができますっていうことなんです。

なので、これで軽くやってみます。

元々の\(△^2\)を左辺に持っていくと、こうなります。

\({(□+△)}^2-△^2=□^2+2□△\)

最初の右辺の係数2で(□+△)を割って、この□を取ってしまって△が残って、そこから\(△^2\)を引くっていうことをやっていきます。

っていうのを、\(ax^2+bx+c=0\)でやってみますか、みたいな発想をしていきます。

なんですけど、多分\(a, b, c\)で平方完成していくの、難しくないですか？だから、図形の方でやっちゃいましょうか。

これ見てる人は多分、平方完成は何回か練習する機会があると思うので「そんなにこれでやらなくてもいいかな…」と思うんですけど。

「2次方程式の解の方式」は、高校では「平方完成」っていうのを習って、それでやると思うんですけど、今回はさっきお話した図を使ってやってみます。

\(ax^2+bx+c=0 (a≠0)\)

さっき見せた例が、\(x^2\)の係数が1の例を見せましたが、今回は\(a\)になっていてこの\(a\)が邪魔になってるっていうのもあるので、1回\(a\)で割っていきます。

\(x^2+\frac{b}{a}x+\frac{c}{a}=0\)

ここから始めていきましょう。1個1個さっきと同じように面積で考えていくという見方でやっていきます。

多分、普通の与えられ方が\(+c\)で書いてあるので、これをそのまま\(a\)で割って\(\frac{c}{a}\)になるので、これを右辺に持っていっちゃうと面積がマイナスになってしまうため、厳密にはこの図で説明するのは変な気がするんですけど、そういう細かいことはちょっと置いといて、さっきの図形を使ってやっていきます。

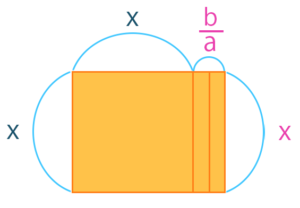
右側の長方形の面積が、最初は\(\frac{b}{a}\)となります。「長方形全体の面積が、左辺になってる」って考えてください。で、ちょっと\(+\frac{c}{a}\)が邪魔だから右辺に持ってきます。

\(x^2+\frac{b}{a}x=-c\frac{c}{a}\)

それからさっきの考え方にのっとって、右端の長方形の部分を半分にして、また下に持ってってあげます。

 

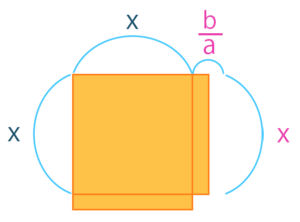
その時に、この\(\frac{b}{a}\)が半分になるっていうのがあって。半分ということは\(\frac{1}{2}\)倍なので\(\frac{b}{a}×\frac{1}{2}\)ですね。

もうなんとなくわかると思うんですけど、次のようになります。

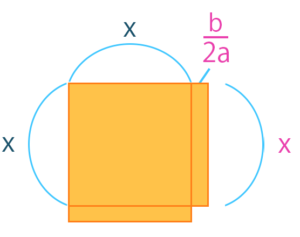
\(\frac{b}{2a}\)っていうのが出てきます。

で、欠けている右下の四角の面積は、\({(\frac{b}{2a})}^2\)になります。これを両辺に加えてあげると、正方形の面積になります。

\(x^2+\frac{b}{a}x+{(\frac{b}{2a})}^2=-\frac{c}{a} = \frac{c}{a}+{(\frac{b}{2a})}^2\)

こんなふうになります。この式で言うと\(x^2+\frac{b}{a}x\)までが、図形の「縦の長さ」と「横の長さ」になります。計算を続けていくと、

\({(x+\frac{b}{2a})}^2=\frac{b^2-4ac}{4a^2}\)

ここで「あれ？\(b^2-4ac\)って見たことあるぞ…？」って高校生は思うかなと思いますが、ひとまず左辺を見てみると2乗の形が平方完成になっているので、平方を取ってあげます。

\(x+\frac{b}{2a}=\pm \frac{ \sqrt{b^2-4ac}}{2a}\)

\(-\frac{b}{2a}\)を移行して、

\(x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)

ということで、これは中学3年生で習う公式ですが、中学校でやる公式の中で多分最も長い公式だと思うんですよ。高校1年生でも「こんな長い公式あったかな？」っていう感じですけど。

解の公式はなんでやたら難しいのかっていうと、分数とルートがあるから厄介なんですね。分数も嫌だし平方根も嫌だし。

だから高校生に授業を教えていると、答えが分数だった場合、生徒の心理としては心配になるんですね。「これ、答えが分数で出てちゃったんですけど…これで答え本当に合ってるんですかね？」って聞いてくるんですね。「いや合ってる時もあるでしょ」っていうことではあるんですけど。

√出てきても気持ち悪いし、分数出てきても気持ち悪い。みんなが好きなのは、やっぱり「整数」なんですよね。答えとして整数が出てくる、綺麗なのがいいらしいです。

だから確率とかの答えは、みんな心配になります。「本当にこの答え、合ってるんでしょうか…？」みたいなね。

っていう感じで、今回は解の公式についてのお話でした。2次方程法程式の解の公式に至るまでに、1,000年かかったのを体感してもらいました。

動画バージョンはこちら→