こんにちは。究進塾 編集部です。
今回の記事は、江口先生「電磁気学 第2回」の最終回です。電場、電位、立体角についての練習問題の解説です。

江口先生の動画解説

はじめに：当記事は、動画で解説をしている内容をご紹介していますが、音声を流せる環境にある方はぜひ動画をご覧いただき、江口先生の授業の雰囲気も一緒に掴んでいただければと思います。

江口和弘講師：「【大学物理】電磁気学 第2回 – Coulombの法則, ベクトル解析の基礎, 電場, 電位,立体角」（所要時間 1:01:49 ）

この記事に該当する箇所：46:21～(分数をクリックすると開始分数箇所から別窓で開きます）

練習問題

今回の最後に、練習問題をいくつかやってみたいと思います。

\(+q\)、\(-q\)の二つの電荷が距離\(2l\)離れておいてある。 (1) 両電荷を結ぶ直線上の電場の強さを求めよ。 (2) 両電荷を結ぶ線分の垂直二等分線上で、電荷を結ぶ中点から距離\(x\)における電場の強さと方向を求めよ。

 

「(1) 両電荷を結ぶ直線上の電荷の強さを求めよ。」

座標軸を、両電荷、\(-q\)と\(+q\)の真ん中に原点Oを取るような座標軸を考えます。そのときに、先述のように\(+q\)による電荷と\(-q\)による電場の足し算になるわけですから、3つの領域によって電場の向きはそれぞれこの図に書いたようになります。

つまりマイナスの電荷には、電場はマイナスに向かうように働くので、青で書いたような矢印になります。そして赤はプラスの電荷なので、ここから出ていくように電場は働くので、赤で書いたような矢印になります。それで各々3つの領域について計算しておくわけですが、このように減点法を取って位置座標\(x\)を取ると、まず\(xE\)の位置の電場は、\(+q\)による電場は左向きに距離が\(l – x\)になるので、\(\frac{q}{4πε_0(l – x)^2}\)、このような電場が左向きに働きます。
\(-q\)による電場は、\(-q\)に入る方向に働きます。この場合の距離は\(l + x\)になるので、\(\frac{q}{4πε_0(l+x)^2}\)となります。

この2つの電場の足し合わせが、この\(+q-q\)の間にある電場ということになります。これを計算すると、それぞれ足すと下記のような式に計算できる、ということになります。

両電荷間
左向きに \(E = \frac{1}{4πε_0} \left\{ \frac{q}{(l-x)^2} + \frac{q}{(l+x)^2} \right\} = \frac{q}{4πε_0} \frac{2(l^2 + x^2)}{(l^2-x^2)^2} \)

次に、\(+q\)の電荷より右の領域を考えます。

\(+q\)による電波は右向きに働きます。大きさはここに書いてあるように距離が\((x-l)^2\)ということになります。

で\(-q\)による電場はマイナスに入っていくわけですが、ここの領域では、\(+q\)による電場と\(-q\)による電場が逆方向にあります。大きさは\(x\)の\(1\)は、これは\(-q\)からの距離が\(x+l\)ですので、\(\frac{q}{4πε_0(x+l)^2}\)となります。で、この電場を2つ足し算してやればいいわけですから、次のように計算できる、となります。

\(q\)の外側
右向きに \(E = \frac{1}{4πε_0} \left\{ \frac{q}{(x-l)^2} – \frac{q}{(x+l)^2} \right\} = \frac{q}{4πε_0} \frac{4xl}{(x^2 – l^2)^2} \)

で、\(x + l\)と\(x – l\)の大きさを考えると、赤の\(+q\)による電場の方が大きいので、この領域の電場は右向きになります。

今度は\(-q\)の左側です。

この場合は\(+q\)から出てくる電場は左向きになりまして、距離が\(x+l\)になります。それから\(-q\)には電場が入っていくので、右向きになりまして、このときの\(-q\)と\(x\)の距離は\(x-l\)になります。で、この2つを足し算してやると、次の計算したような式になります。

\(-q\)の外側
右向きに

\(E = \frac{1}{4πε_0} \left\{ \frac{q}{(x-l)^2} – \frac{q}{(x+l)^2} \right\} = \frac{1}{4πε_0} \frac{4xl}{(x^2-l^2)^2}\)

この場合は\(x-l\)の方が当然\(x+l\)より小さいわけですから、この領域の電場は右向きに向くということになります。

以上をまとめると次のようになります。

このように\(+q\)と\(-q\)の間のでは電場を左向きに働き、大きさは\(\frac{q}{4πε_0}\frac{2(l^2 + x^2)}{(l^2 – x^2)^2}\)になります。
\(-q\)の外側では右向きに働き、大きさは\(\frac{q}{4πε_0} \frac{4xl}{(x^2-l^2)^2}\)となります。
そして右側の領域では、電場はやっぱり右向きに働いて、大きさは\(\frac{q}{4πε_0} \frac{4xl}{(x^2-l^2)^2}\)となります。
これをグラフにして右向きを正としてグラフに書きますと、次のようなグラフになります。

これが、\(+q\)と\(-q\)を結ぶ線分上での電場の大きさということになります。

 

「(2) 両電荷を結ぶ線分の垂直二等分面上で、電荷を結ぶ中点から距離\(x\)における電場の強さと方向を求めよ。」

「電場を求めなさい」と言うんですが、縦軸上の電場を求めるわけですから、これを\(x\)と置いて計算していきます。

そうすると、\(+q\)が作る電場は、赤矢印の部分、ここの向きに\(E+\)というこういう電場を作ります。そして大きさは距離が三平方の定理を使えると\(l^2+x^2\)の√が距離になるので、\(E_+\)の大きさは\(E_+ = \frac{1}{4πε_0} \frac{q}{l^2 + x^2}\)となります。

マイナスの電荷の作る場合はマイナスに入っていくわけですから、青の矢印の向きになります。大きさは対称性から全く同じ向きになります。ただ、向きだけが違うということです。
で、この点の電場を求めます。これを足し算するわけですが、先述のように電場はベクトルなので、これをベクトルで足し算します。

するとこうなります。そうすると、この緑の線で示したようなのが合成の電場になり、これは対称性から考えて菱形の対角線になるので、左向きの電場になります。
で、計算すると\(E = E_+ \frac{2l}{(l^2 + x^2)^{1/2}}\)という式になり、これを計算していくと、次のようになります。

\(E = E_+ \frac{2l}{(l^2 + x^2)^{1/2}} = \frac{1}{4πε_0} \frac{q}{l^2+^2} \frac{2l}{(l^2+x^2)^{1/2}}\)
\(= \frac{1}{4πε_0} \frac{2ql}{(l^2 + x^2)^{3/2}}\)

それでこれを、どんな大きさかをグラフで書いてみると、次のようなグラフになります。

ここにあるときが電場が一番大きくて、離れれば離れるほど小さくなっていき、向きは常に左に正＝左向きというような電場ができることになります。

 

練習問題３

一様な線密度λの電荷が線分上に分布している、Pから線分に卸した垂線の足をOとすると、\(\overline{OP} = a\) である。 （１）Oを原点として線分に沿って座標をとる。線分の両端の座標が\(l1\)・\(l2\)のときのP点の電位を求めよ。 （２）Pが線分の中点の場合の電位、および電場の強さを求めよ。 （３）無限に長い直線の場合の電場の強さを求めよ。

(1)の解説
「Oを原点として線分に沿って座標をとる。線分の両端の座標が\(l1\)・\(l2\)のときのP点の電位を求めよ。」ということです。

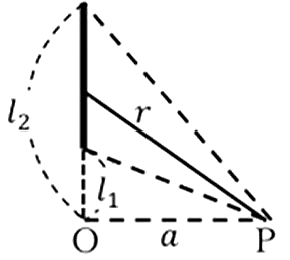
先ほどのように、ここに非常に微小な長さの電場、線要素\(ds\)を考えるわけですね。

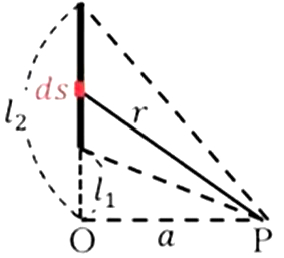
そこには\(λds\)という電荷があるので、これを電場、点電荷として考えて、これを\(l1\)から\(l2\)まで積分してやればいい。

\(V=\frac{1}{4πε_0}\ ∫ \frac{λds}{r}\)

これを計算してやればいいということになります。

\(V=\frac{1}{4πε_0}\ ∫ \frac{λds}{r}\)=\(\frac{1}{4πε_0}\displaystyle\int_{l_1}^{l_2}\)\(\frac{λds}{\sqrt{s^2+a^2}}\)

 

さてここで、ここの積分（\(\frac{λds}{\sqrt{s^2+a^2}}\)）なんですが、この積分が問題になるわけです。これ、色々な積分の計算方法はあるのですが、１つの定石として\(s^2＋a^2\)があるので、「\(s＝\ a\ tanθ\)と置換する」という方法はあります。それで計算してもいいんですが、非常に計算量が多くなってしまいます。

この積分は、\(s+ \sqrt{s^2+a^2}=t\)と置換すると非常に楽にできまして、途中は省略しますけれども、これ積分すると、\(\ ∫ \frac{ds}{\sqrt{s^2+a^2}}\ = log (s + \sqrt{s^2+a^2}) + c)\)、このようになります。これは高校の数学Ⅲで出てくる中では難易度が高い部類の置換積分になるわけですが、このように大学に入ってくると平気でこういう積分が出てくることになります。

なので積分はこう計算できるので、\(l_1\)から\(l_2\)まで積分すると、電位分布は、ここに示したように計算できます。

\(= \frac{λ}{4πε_0}\ log \frac{l_2+\sqrt{l_2^2 + a^2}}{l_1 + \sqrt{l_1^2 + a^2}}\)

 

(2)の解説
「Pが線分の中点の場合の電位を求めなさい」ということですので、この場合は中点ですので以下のように座標配置を考えます。

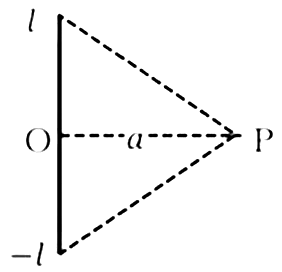
そうすると、先ほど計算した\(l_1\)を\(-l\)、\(l_2\)を\(l\)と置き換えればいいわけですから、単純に\(= \frac{λ}{4πε_0}\ log \frac{l_2+\sqrt{l_2^2 + a^2}}{l_1 + \sqrt{l_1^2 + a^2}}\)の\(l_1\)を\(-l\)、\(l_2\)を\(l\)と置き換えるだけで計算できます。

でそれを計算してみますと、単に代入するだけなので、次のような式になります。

V\(=\frac{λ}{4πε_0} log \frac{l + \sqrt{l^2 + a^2}}{-l + \sqrt{l^2 + a^2}}\)

もう１つ、今度の場合は「電場の強さを求めなさい」ということなので、これは\(l\)だけの式になってますので、電場は計算していくとこのようになります。

\(= \frac{λ}{2πε_0} log \frac{l + \sqrt{l^2 + a^2}}{a}\)

電場はさっき言ったように\(a\)の方向、対称性から右向き、水平方向のこともわかっていますので、これを\(a\)で微分してマイナスを取れば電場は計算できます。

\(E = -\frac{∂V}{∂a}\)

で、この微分はその難しくない微分ですので計算すると、このように計算できるということになります。

\(= \frac{λ}{2πε_0} \frac{l}{a\sqrt{l^2 + a^2}}\)

 

(3)の解説
最後に今は有限の線分布を考えたんですが、「これが無限に流れる場合の電場はどうなりますか」っていうことが(3)の問題ですが、(2)で、この場合の電場を\(E = -\frac{∂V}{∂a} = \frac{λ}{2πε_0} \frac{l}{a\sqrt{l^2 + a^2}}\)のように計算したわけですから、無限遠に持ってくる場合は\(l\)を無限大に持っていけばいいと、いわゆる\(l\)の極限を取ればいい（\(l\)→∞）ということになりますので、\(E\)を持ってくるとこれはこの極限\(\frac{l}{a\sqrt{l^2 + a^2}}\)を取ればいいということになります。この極限も難しい極限ではないので計算すると、

\(E= \frac{λ}{2πε_0a}\)

のようになります。

 

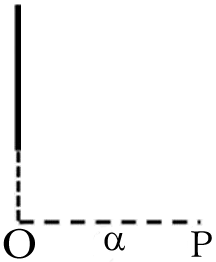
練習問題４ Oを頂点とする半頂角\(a\)の一つの錘面できりとられる面の立体角を求めよ。

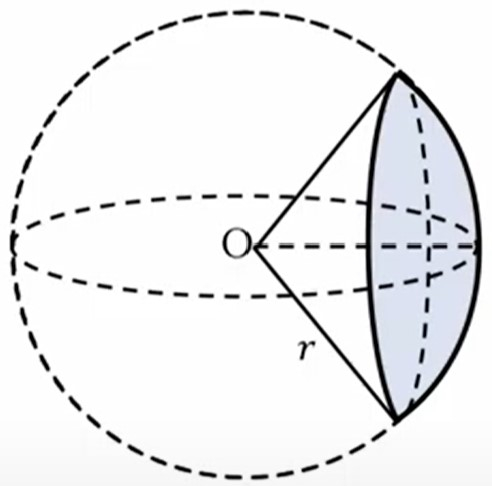
先ほど立体角導入しましたが、この後、いくつか続いていくので、この立体角を求めてみたいと思います。「Oを頂点とする球の、半頂角\(α\)の球を切り取ったような面、この青で塗った面をOから見込んだときの立体角はいくつですか」ということを計算します。そうすると、次のように赤で囲ったドーナツ状の領域を「微小な\(dS\)」と考えます。

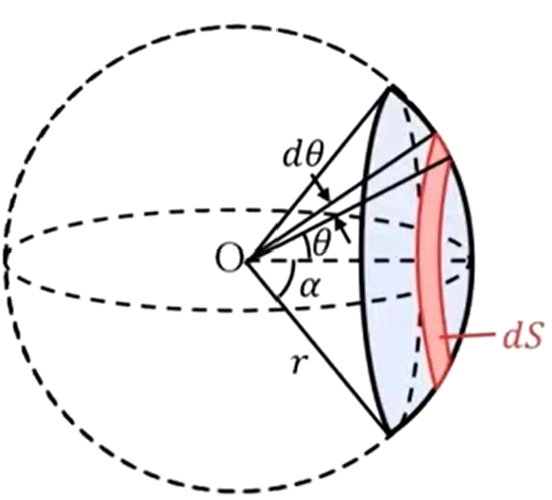
そうするとoから\(dS\)までの角度が微小な\(dθ\)になりますので、これをわかりやすく書いてみます。この赤の部分を平らにしてみると、このようなドーナツ型になります。

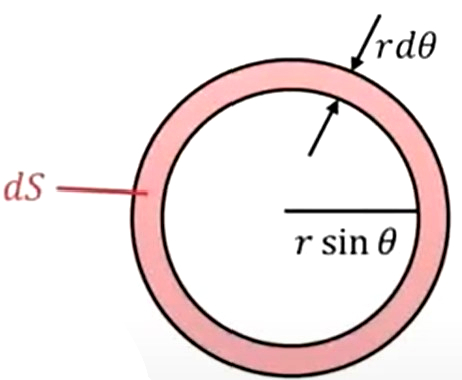
半径は\(r \ sinθ\)、幅が\(rdθ\)ということになります。なので単純にこれは、中心の円周の長さに幅を掛ければ面積になります。\(ds\)は、長さ\(2π (r\ sinθ)\)に幅\(rdθ\)を掛ければいいということで、この赤の部分の面積は、

\(ds = 2π(r\ sinθ)rdθ\)
\(= 2πr^2 sinθ \  dθ\)

ということになります。で、これで立体角を計算するわけですが、\(ω\)は\(\frac{dS}{r^2}\)、これを積分することによって計算できます。

\(ω = \int\frac{dS}{r^2}\)

で、\(dS\)をそのままこの式に代入してやりますと、

\(=\int_{o}^a \frac{2πεr^2 \ sinθ \ dθ}{r^2}\)

で、\(r^2\)はキャンセルされますので\(=2π \int_{o}^a \ sinθ \ dθ\)、これは単純に「\(sin θ\)の積分」ということになりまして、この場合は立体角は\(2πr\)なので、円錐状の形ですね、これ半頂角が\(α\)ある場合の立体角は

\(=2π(1-cosα)\)

このような形になります。これはこの後もいくつか使っていくことになります。

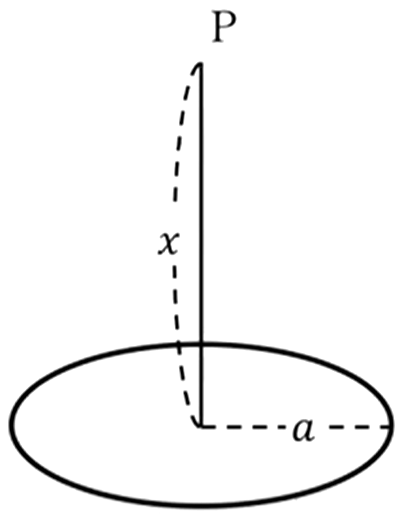
練習問題５ 半径\(a\)の円板に面密度σで電荷が一様に分布しているとき、円板の中心軸上中心から\(x\)の距離の点Pでの電位および電場を求めよ。

それから、今度は面分布してる場合の例です。これは半径\(a\)の円盤、「ここに入ってる円盤状に一様に面密度\(σ\)、単位面積当たり\(σ\)の電荷が分布してますと。でこのように、このときにこの円盤の中心から垂直に\(X\)離れたところでの電位と電場を求めなさい」という問題です。

まず電位を求めますが、どうやって求めるかというと先ほどと似てるんですが、これもここで赤で書いたような面積要素を考えます。

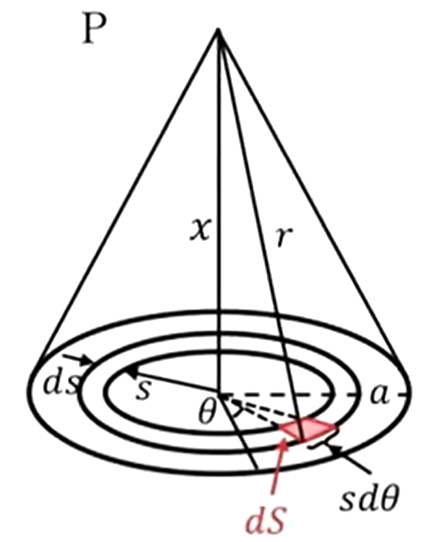
このところ面積は幅が\(dS\)で誇張が半径×小さい角\(dθ\)になりますので、ここに書いてあるように、赤で書いた部分の面積は、\(dS = sdsdθ\)だと計算できるわけです。

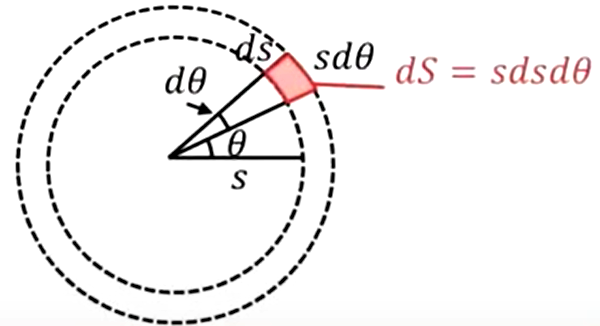
で、これにσをかけたのが電荷ですので、これを点電荷として積分して計算してやります。この場合は\(s\)と\(θ\)、\(θ\)方向と\(r\)方向と両方向に積分してやりますので、重積分になります。

\(V =\frac{1}{4πε_o} \int \frac{σdS}{r}\)
\(=\frac{1}{4πε_o} \int_{o}^{2π} \int_{o}^a \frac{σsdsdθ}{\sqrt{s^2 + x^2}}\)

で、これを計算すると、分けてやると積分自身は難しくないのですが、このような積分形になります。

\(= \frac{σ}{4πε_0} \int_{0}^{2π} dθ \int_{0}^a \frac{sds}{\sqrt{s^2 + x^2}}\)

こちらの積分は単純に\(1\)の積分だから問題ないと思います。で左側の場合も、この場合は先ほどと違って上に\(s\)があるので、単純にこれ\(s^2 + x^2\)を置換すれば簡単に積分できるので、この積分も問題なく計算できます。

ので、これ計算すると、このような形に計算できます。

\(= \frac{σ}{2ε_0} ( \sqrt{a^2 + x^2} – x\))

で、その次に電場を計算するわけですが、これも対称性から考えて下図の緑矢印方向に電場が働いていると必ず反対側の電場（青矢印）がはたらいているわけです。

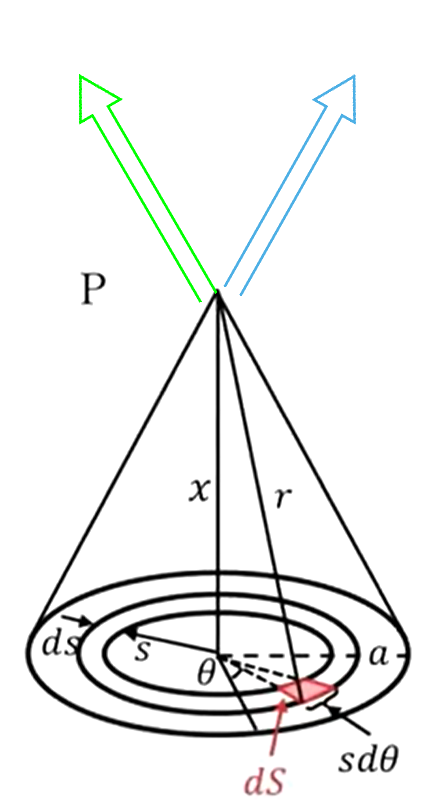
ですから、水平方向はキャンセルして、電場は常に垂直上方向に向くことになります。なので、電位を\(x\)で微分してマイナスをつけてやれば電場は計算できるということになります。

\(E = – \frac{∂V}{∂x}\)

この微分も難しい部分ではないので計算してやると、このような形になります。

\(=\frac{σ}{2ε_0}(1 – \frac{x}{\sqrt{a^2 + x^2}}\))

そうすると、\(\frac{x}{a^2+x^2}\)というのは\(\frac{x}{r}\)になるわけですから、これは

\(= \frac{σ}{2ε_0} (1 – cos \ α)\)

ということになります。そうすると、先程のように立体角で見ると、この立体角は\(ω = 2π(1 – cos α)\)で表されるわけですから、この立体角を用いてやると、

\(=\frac{σ}{4πε_0}ω\)

というふうに計算できます。このように、立体角を使うと、非常にシンプルな形で表現できる、というのが特徴になります。

 

---

 

関連記事：【大学物理】電磁気学シリーズ

第1回 – 静電気、帯電、静電誘導、誘電分極 –
第2回-【大学物理】電磁気学 第2回① – Coulombの法則
第2回-【大学物理】電磁気学 第2回② – ベクトル解析の基礎（電場、電位に必要な数学）
第9回 – 静電容量(コンデンサー) –