こんにちは。究進塾 編集部です。
今回の記事は、江口先生「電磁気学 第2回」の続きです。電位を勉強する前に必要な数学について解説します。

江口先生の動画解説

はじめに：当記事は、動画で解説をしている内容をご紹介していますが、音声を流せる環境にある方はぜひ動画をご覧いただき、江口先生の授業の雰囲気も一緒に掴んでいただければと思います。

江口和弘講師：「【大学物理】電磁気学 第2回 – Coulombの法則, ベクトル解析の基礎, 電波, 電位,立体角」（所要時間 1:01:49 ）

この記事に該当する箇所：10:23～22:45（分数をクリックすると開始分数箇所から別窓で開きます）

電磁気学が苦手になる人がいますが、電磁気学がわからなくなってしまうポイントは、大体2つあります。

①電気が目に見えないものだから概念がつかみにくい。
②高校のときと違って、高度な数学を使って記述していくので、数学がわからなくてちんぷんかんぷんになってしまう。

今回は、ここで使う範囲に限りますが、必要な数学のところだけおさらいします。

ベクトル

①内積（スカラー積）

内積は高校でやっている範囲なので、深く説明はしませんが、以下のようになります。

\(A・B = AB cosθ\) \(　　  = A_x B_x +A_y B_y +A_z B_z\)

内積のことを、別名「スカラー積」と言います。スカラーはベクトルに対して使われる言葉で、向きを持っておらず、大きさだけを持っている積です。

内積は、計算した結果ベクトルではない（大きさしか持っていない）ので、スカラー積と言います。また、「\(A・B\)」のように記号として「・（ドット）」を使うので「ドット積」とも言います。

②外積（ベクトル積）

内積があるから当然「外積」という言葉もあるわけですが、これは高校のときには出てこなかった概念です。

\(A×B=\begin{vmatrix}
e_x & e_y & e_z \\
A_x & A_y & A_z \\
B_x & B_y & B_z \\
\end{vmatrix}\)

上の「\(A×B\)」のように、外積は記号では「\(×\)」を使うので、この結果を結論から先に言うとベクトルになります。そのため「ベクトル積」、もしくは掛け算の記号を使うので「クロス積」と言います。

大きさを求める AとBと外積というのを求めようとすると、まず大きさ自身はAとBが張る平行四辺形の面積、具体的に書くと\(S = AB sin θ\)これが「外積のベクトルの大きさ」になります。
向きを求める 向きは、AからBに右ねじを回した時に進方向なので、外積は・Aにも垂直 ・Bにも垂直という方向を向くことになります。なので当然、外積の場合は逆向きの交換法則を計算してみると、\(B×A\)は向きが逆向きになってしまうので、これは\(A×B\)と一致しません。なので、外積の場合は交換法則は成り立ちません。もっと言うと、これは単に向きが変わるだけなので\(-A×B\)は外積です。 ・\(B×A ≠ A×B\) ・\(B×A = -A×B\)	向きを求める 下図のように逆向きになってしまうので、交換法則は成り立たない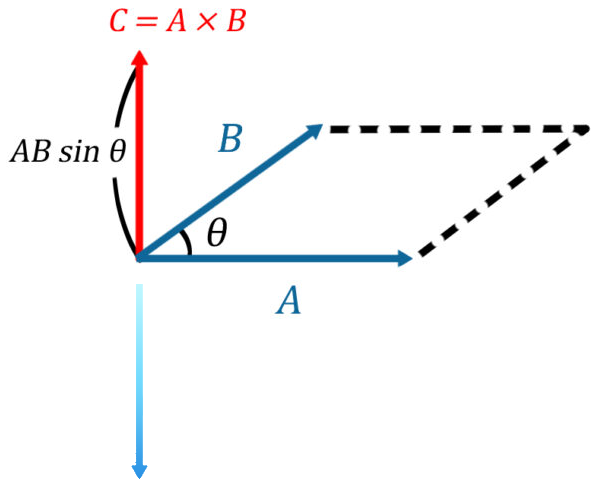

これは電磁気学では色々なところで使っていくので覚えておいてください。

ではこれを成分で表すとどうなるかというと、行列の形を取らせてもらっていますが、成分表示は以下のようになります。

\(A×B=\begin{vmatrix}
e_x & e_y & e_z \\
A_x & A_y & A_z \\
B_x & B_y & B_z \\
\end{vmatrix}\)

ここで\(e_x、e_y、e_z\)と書いているのは、「\(x\)軸、\(y\)軸、\(z\)軸方向に沿った単位ベクトル（大きさ1のベクトル）」です。この値を計算する方法がありますので、おさらいしておきます。

行列の計算方法

一般的に行列式の値には、3つ数字が並んでいます。

\(\begin{vmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
\end{vmatrix}\)

右上がりに全て掛けます。 \(a_{11} \)は\(a_{22} \)と\(a_{33} \)、 \(a_{12} \)は\(a_{23} \)と、その先がないので回って\(a_{31} \)、 \(a_{31} \)は同様に先がないので\(a_{23} \)、\(a_{12} \)と掛けます。 右下がりの場合は、符号は全部「＋」です。 マイナスの場合は、左下がりになります。符号はマイナスです。

これを掛け算したものを全部足したものが、行列の式の値になります。こういう計算の仕方があります。

この例で、外積を成分表示で計算してみる、ということをやってみます。

\(A×B=\begin{vmatrix}
e_x & e_y & e_z \\
A_x & A_y & A_z \\
B_x & B_y & B_z \\
\end{vmatrix}\)

これを全部展開する
\(e_x\)のベクトルが絡む方向は、1つは右下がりの方向です。右下がりは「プラス方向」でしたので「\(A_yB_z\)」です。もう1つは左下がり「マイナス方向」の部分なので「\(-A_zB_y\)」です。プラス方向、マイナス方向の両方ともに「\(e_x\)」が入っているので、式は

\(=(A_yB_z – A_zB_y) e_x\)

となります。

同じように\(y\)が絡むところの右下がりと左下がり（\(y\)成分）、\(z\)が絡むところの右下がりと左下がり（\(z\)成分）を計算していくと、

\(=(A_yB_z – A_zB_y) e_x\)
\(+(A_zB_x – A_xB_z)e_y\)
\(+(A_xB_y – A_yB_x)e_z\)

成分表示すると、行列形式で書きましたが、全部展開してしまうとこういう式になります。これがなかなか大変ですが、ここはよく使っていくので理解しておいてください。

スカラー3重積とベクトル3重積

この2つは今のところあまり使わないので、詳しい説明は今回は省きます。簡単に言うと、次のようになります。

①スカラー3重積

「\(A\)、\(B\)と\(C\)の外積」ですが、外積「\(B × C\)」はベクトルです。そして\(A\)もベクトルですが、これは内積を取っているので、結果がスカラーになるので「スカラー3重積」と呼びます。その結果は先程の行列を使って表すと、上記のようになります。

これは幾何的には少し意味を持っていて、「この大きさって何か？」というと、

\(A\)というベクトル \(B\)というベクトル \(C\)というベクトル

この3つのベクトルで張ったときの平行四面体を作ったときの「体積の大きさ」になります。

②ベクトル3重積

スカラー3重積に対し、ベクトル3重積は\(A・B・C\)を全て外積を取ったものです。

\(A × ( B × C  )\)

外積を取ったので\(B × C\)はベクトル、そして\(A\)もベクトルです。ベクトルとベクトルの外積なので、結果はベクトルになります。結果は、

\(A × ( B × C ) = B ( A ・ C ) – C ( A・B )\)

という公式があります。

ベクトルの微分演算

ここが、電磁気学をとても大変にしている数学のところです。ベクトルの解析の分野で「微分演算」というのがあります。

〇微分演算子

「∇」という記号があり、これは「ナブラ」と読みます。∇は以下のように定義されます。

\(∇ = \frac{∂}{∂_x}\ e_x + \frac{∂}{∂_y}\ e_y + \frac{∂}{∂_z} e_z\)

∂の記号は、偏微分を表す記号です。

\(x\)方向、\(y\)方向、\(z\)方向のとき、それぞれ表しています。このとき、

\(\frac{∂}{∂_x}\)

このように微分演算をしています。

\(\frac{∂}{∂_x}\)は、\(x\)を掛けている、いわゆるベクトルライクなように表現しているわけです。これを「微分演算子」と言っています。これをいろんなものに掛けます。

①スカラー\(φ\)の勾配

1つは、この微分演算子をスカラー量「\(φ\)（ファイ）」に掛けた時です。これは別の言い方をすると「grad \(φ\)（グラッド ファイ）」という書き方もしています。

そうするとこれは単純にスカラー量\(φ\)を∇に書ければいいわけですから、

\(∇φ = gradφ =\) \(\frac{∂φ}{∂_x} e_x + \frac{∂φ}{∂_y} e_y + \frac{∂φ}{∂_z} e_z \)

となります。

②ベクトルAの発散（湧き出し）

それから、ベクトルにナブラを内積で作用させる場合、これは「div A（ divergence A）」とも書きます。これは、内積になってしまうので、結果としては方向を持たない量になってしまいます。結果的に、

\(∇A = divA = \frac{∂A_x}{∂_x} + \frac{∂A_y}{∂_y} + \frac{∂A_z}{∂_z}\)

となります。これは「発散」と言って、いわゆる「湧き出し」というものを表しています。

③ベクトルの回転

もう1つ、∇という微分演算子を外積でAに作用させます。このことを「rot（rotation）」または「curl」と書く教科書もあります。これは結果的に、行列で全部成分を表してやると、以下の様になります。

\(∇× A = rotA = curl A\begin{vmatrix}
e_x & e_y & e_z \\
\frac{∂}{∂_x} & \frac{∂}{∂_y} & \frac{∂}{∂_z} \\
A_x & A_y & A_z \\
\end{vmatrix}\)

④ラプラシアン

もう1つ重要な要素として「ラプラシアン」という微分演算子があります。

\(△ = ∇^2 = ∇・∇ = \frac{∂^2}{∂x^2} + \frac{∂^2}{∂y^2} + \frac{∂^2}{∂z^2}\)

これは∇を2回掛けたもので、∇と∇の内積と考えるわけですが、

\((\frac{∂}{∂x} e_x + \frac{∂}{∂_y} e_y ) + \frac{∂}{∂_z} e_z\)

これを2つ掛け合わせるわけです。内積なので、成分同士を掛け合わせれば良い、という話になるので、

\(=\frac{∂^2}{∂^x} + \frac{∂^2}{∂y^2} + \frac{∂^2}{∂z^2} \)

このようになります。これはあくまでも\(x\)、\(y\)、\(z\)という直交座標で表示した話ですが、これはのちのち色々な計算で使っていきます。

以上が、今回の解説で使っていく、電磁気学に必要な数学です。

関連記事：【大学物理】電磁気学シリーズ

第1回 – 静電気、帯電、静電誘導、誘電分極 –
第2回-【大学物理】電磁気学 第2回① – Coulombの法則
第9回 – 静電容量(コンデンサー) –