こんにちは。究進塾 編集部です。
江口先生の電磁気学の解説シリーズの第3回です。今回は、多重極とそれによる電位を考えていきます。

江口先生の動画解説

はじめに：当記事は、動画で解説している内容をご紹介していますが、音声を流せる環境にある方はぜひ動画をご覧いただき、江口先生の授業の雰囲気も一緒に掴んでいただければと思います。

江口和弘講師：「【大学物理】電磁気学 第3回 – 多重極とそれによる電位」（所要時間 37:59 ）

今回の解説の流れ

多重極とそれによる電位を解説するにあたり、数学的補足として、極座標とその微分演算子の話を、最初に少し解説します。そして、その後に多重極の話をしていきます。

極座標（2次元）

🔵極座標

まず極座標です。

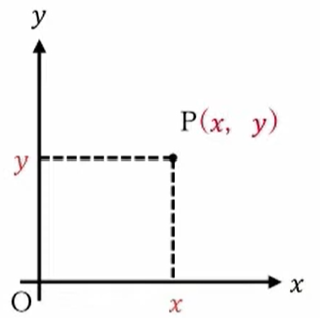
今回は2次元に限った場合の話をしますが、一般に、直交座標を\(xy\)で表した場合に、点Pを\(xy\)で表しているわけです。これを極座標で表すと、このようになります。

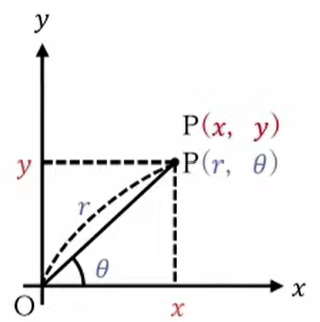
この角度変化の\(θ\)と原点間の距離\(r\)で表します。これは数学Ⅲでも出てくる範囲ですが、このように\(r\)と\(θ\)でも点は表すことができます。これが2次元の曲座標です。

で、\(xy\)と\(rθ\)の関係には、それぞれ次の式のようになります。

\(x = r \ cos θ\)　\(r = \sqrt{x^2 + y^2}\)
\(y = r \ sin θ\)　\(θ = tan^{-1} \frac{y}{x}\)

\(r\)と\(θ\)を\(xy\)で表すと、\(r\)は三平方の定理で\(r = \sqrt{x^2 + y^2}\)、\(θ\)は\(θ = tan^{-1} \frac{y}{x}\)です。

大丈夫だと思いますが、これは「タンジェントの逆関数」です。このように表すことができるわけです。

 

🔵基底ベクトル

次に、ベクトルで位置を表すのですが、\(xy\)座標の場合は基底ベクトルです。

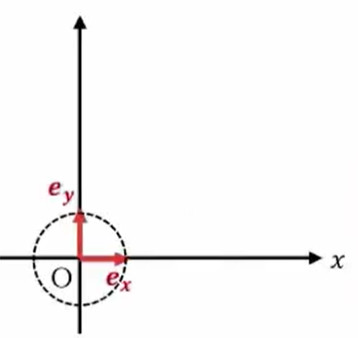
基準となるベクトルを、\(x\)軸に沿った長さ\(1\)の単位ベクトル\(e_x\)と、\(y\)軸に沿った長さ\(1\)の単位ベクトル\(e_y\)、この2つで表していくわけです。

極座標の場合、点Pにある座標\(e_r\)という基底ベクトル（大きさ\(1\)のベクトル）ですが、これは\(r\)のみが変化して\(θ\)が変化しない方向に向けて取ります。

そして\(eθ\)は、これも大きさは\(1\)ですがやはり\(r\)は変化せず、\(r\)は一定で、\(θ\)だけが変化することになります。

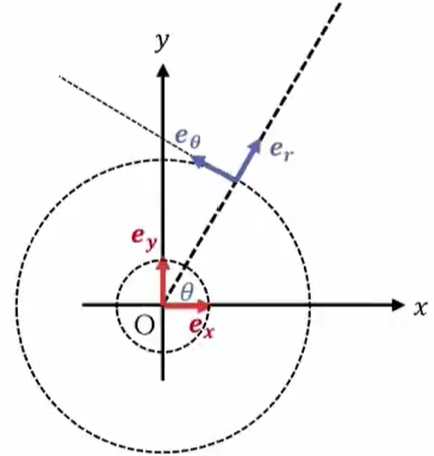
そうするとこのような向きになって、これは直交することになります。

ここで1つ注意が必要です。\(e_x\)と\(e_y\)の場合、点Pがどこにあっても絶対変わらないベクトル（定ベクトル）なのですが、\(e_r\)と\(e_θ\)は点Pの位置によって大きさは\(1\)ですが、向きが変わります。例えば、\(x\)軸の少し上のあたりを考えた場合、\(e_r\)は右斜め上方向へ向き、\(e_θ\)は上方向の向きのことになりますから、\(e_r\)と\(e_θ\)は\(e_x \ e_y\)と違って定ベクトルではありません。位置によって変わる、ということに注意が必要です。

で、この\(e_rx\)を原点の方に平行移動すると、このような感じになります。

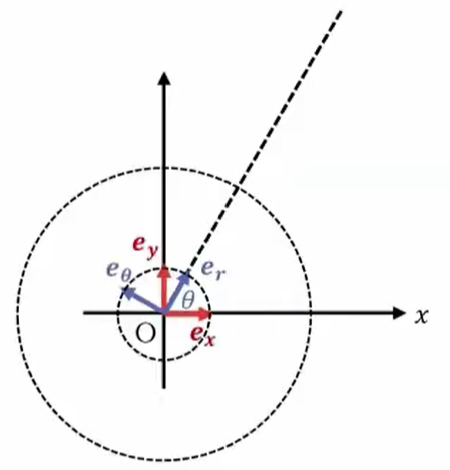
\(e_x\) \( e_r\)と、\(e_r\) \(e_θ\)の関係を求めることができるわけです。

\(e_x = cos \ θ \ e_r \ – \ sin \ θ \ e_θ\)
\(e_y = sin \ θ \ e_r \ + \ cos \ θ \ e_θ\)

\(e_r = cos \ θ\ e_x \ + \ sin \ θ \ e_y\)
\(e_θ = \ – sin \ θ \ e_x + \ cos _ θ \ e_y\)

ここに書いたように、\(e_x\)と\(e_y\)を\(e_r\)と\(e_θ\)で表すと\(e_y = sin \ θ \ e_r \ + \ cos \ θ \ e_θ\)、逆に\(e_r\)と\(e_θ\)を\(e_x\)と\(e_y\)で表すと\(e_θ = \ – sin \ θ \ e_x + \ cos _ θ \ e_y\)、このようになります。これは上の図のところで成分を取ってやって計算すれば、簡単に求めることができます。

で、これを行列表記すると、以下のような表記をすることができるわけです

\(
\left(
\begin{array}{crl}
cos \ θ & -sin \ θ\\
sin \ θ & cos \ θ
\end{array}
\right)^{-1} =
\left(
\begin{array}{crl}
cos \ θ & sin \ θ\\
-sin  \ θ & cos \ θ
\end{array}
\right)\left(
\begin{array}{crl}
e_x\\
e_y
\end{array}
\right)= \left(
\begin{array}{crl}
cos \ θ & -sin \ θ\\
sin \ θ & cos \ θ
\end{array}
\right) \left(
\begin{array}{crl}
e_r\\
e_θ
\end{array}
\right)\)

\(
\left(
\begin{array}{crl}
cos \ θ & sin \ θ\\
-sin \ θ & cos \ θ
\end{array}
\right)^{-1} =
\left(
\begin{array}{crl}
cos \ θ & -sin \ θ \\
sin \ θ & cos \ θ
\end{array}
\right)\left(
\begin{array}{crl}
e_r\\
e_θ
\end{array}
\right) = \left(
\begin{array}{crl}
cos \ θ & sin \ θ\\
-sin \ θ & cos \ θ
\end{array}
\right) \left(
\begin{array}{crl}
e_x\\
e_y
\end{array}
\right)\)

\(\left(
\begin{array}{crl}
cos \ θ & -sin \ θ\\
sin \ θ & cos \ θ
\end{array}
\right)\)と\(\left(
\begin{array}{crl}
cos \ θ & sin \ θ\\
-sin \ θ & cos \ θ
\end{array}\right)\)のところを、いわゆる「回転行列」とも言うわけですが、これらの関係はお互いに逆行列の関係になっています。簡単に行列表記すると、こういうことになります。

🔵微分演算子∇の極座標表示（2次元）

ここで「微分演算子∇を極座標で表したい」ということを考えるわけですが、目的は、今回の多重極展開のところで極座標で表した弦を求めたいので、\(∇f = \frac{∂f}{∂r}e_r \ +\frac{1}{r} \frac{∂f}{∂θ} e_θ\)が使いたい。これを出すところが目的です。

以下は、全部、微分演算子が「2次元の極座標で表すとどうなりますか」という結論だけを書いてある式です。

\(∇= \frac{∂}{∂_r} e_r \ + \ \frac{1}{r} \frac{∂}{∂θ} e_θ\)
※ \(∇ = \frac{∂}{∂_r}e_r \ + \frac{∂}{∂θ}e_θ\)ではない！

\(∇^2 \ = \ Δ \ = \frac{∂^2}{∂r^2} + \frac{1}{r} \frac{∂}{∂_r} + \frac{1}{r^2} \frac{∂^2}{∂θ^2}\)
※\(∇^2 \ = \ \frac{∂^2}{∂r^2} + \frac{∂^2}{∂θ^2}\)ではない！

 

\(∇f = \frac{∂f}{∂r}e_r \ +\frac{1}{r} \frac{∂f}{∂θ} e_θ\)

\(∇・A = \frac{1}{r}\lbrace \frac{∂}{∂_r}(rA_r) + \frac{∂A_θ}{∂θ}\rbrace\)
\(Δf = ∇^{2}f = \frac{∂^{2}f}{∂r^2} + \frac{1}{r} \frac{∂f}{∂r} + \frac{1}{r^2} \frac{∂^2 f}{∂θ^2}\)

注意が必要なのは、直交座標の時は\(∇ = \frac{2}{∂x} e_x + \frac{∂}{∂y} e_y\)で良かったわけですが、極座標で表すと\(∇ = \frac{∂}{∂_r}e_r \ + \frac{∂}{∂θ}e_θ\)ではないということです。

それは何故そういうことが起こるのかというと、先ほど述べたように\(e_r \ e_θ\)が定ベクトルではないからということになります。これを計算していきます。

いろんな計算をしていきますが、 非常に計算量が多い計算になりますので、使うものだけを先に用意しておきます。

🔵使うもの

\(\frac{∂}{∂x} = \frac{∂}{∂r} \frac{∂r}{∂x}+\frac{∂}{∂θ} \frac{∂θ}{∂x}\)
\(\frac{∂}{∂y} = \frac{∂}{∂r} \frac{∂r}{∂y} + \frac{∂}{∂θ} \frac{∂θ}{∂y}\)

まず\(x\)であるものを微分した\(\frac{∂}{∂x}\)というのを考えます。

これは数学の偏微分のところの基礎で出てくるように、変換すると上の式のように表すことができる、というのが数学で出てくる話です。

この偏微分の記号というのはよく出てきまして、\(\frac{∂}{∂r} \frac{∂r}{∂x}\)の\(∂r\)を約分すると\(\frac{∂}{∂x}\)になるわけです。そのような形に変数していく、というようなことを使います。

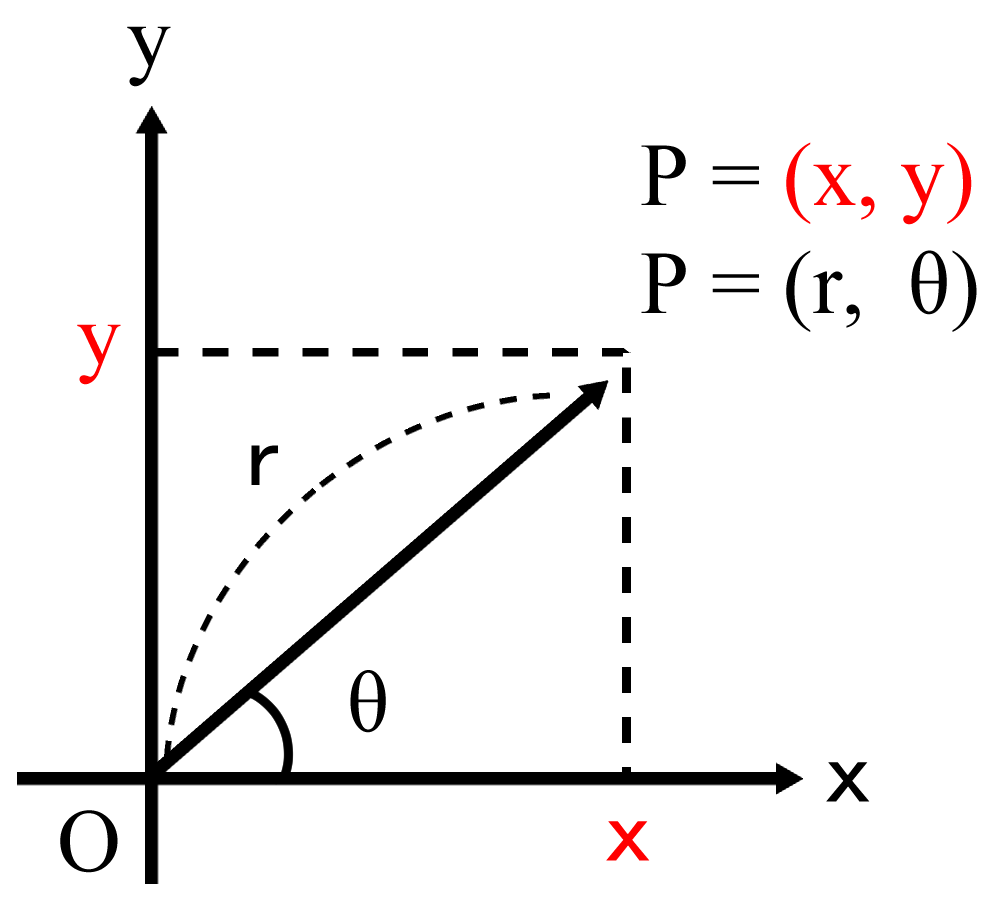
\(x = r \ cosθ\)　\(r = \sqrt{x^2 + y^2}\)
\(y = r \ sin \ θ\)　\(θ = tan^{-1}\frac{y}{x}\)

 

次に、先ほど書いたように\(xy\)と\(rθ\)はこのような関係があります。

なのでこれを微分しなければいけないので、例えば\(r\)を\(x\)で偏微分すると、

\(\frac{∂_r}{∂_x} = \frac{x}{ \sqrt{x^2 + y^2}}= \frac{x}{r} = \frac{r \ cos \ θ}{r} = cos \ θ\)

これを偏微分すると\(\frac{r \ cos \ θ}{r}\)なので\(cos θ\)になります。同じように、\(r\)を\(y\)で微分すると、\( sin \ θ\)になります。これは簡単に計算できます。

\(\frac{∂r}{∂y}=\frac{y}{\sqrt{x^2+y^2}}=\frac{y}{r}=\frac{r cos θ}{r} = sin θ\)

今度は逆に\(θ\)を\(x\)で積分すると、

\(\frac{∂θ}{∂x}\ = \frac{-\frac{y}{x^2}}{1+(\frac{y}{x})^2} = \frac{-y}{x^2+y^2} = \frac{-r \ sin \ θ}{r^2} = -\frac{sin \ θ}{r}\)

\(θ\)を\(y\)で微分すると、

\(\frac{∂θ}{∂y}\ = \frac{\frac{1}{x}}{1+(\frac{y}{x})^2} = \frac{x}{x^2+y^2} = \frac{r \ cos \ θ}{r^2} = \frac{cos \ θ}{r}\)

このような形になります。ここで使っているのは\((tan^{-1}x)^1 = \frac{1}{t+x^2}\)という公式です。これは高校では出てこないのですが、大学ではもう数学で既に出てきていると思います。数学の範囲でも逆関数の微分を使えば、これは簡単に計算できるのですが、これを使います。

その次に、先ほど基底というのを導入して\(e_x\)・\(e_y\) と\(er\)・\(rθ\)の関係、あるいは\(e_r\)・\( e_θ\)と\(e_x\)・\(e_y\)の関係には「こんな関係があるんだよ」という説明をしたのですが、\(e_r\)・\(e_θ\)は定ベクトルではないので、これの微分ということをやらなければいけなくなります。なので、この微分を考えます。

その前に\(e_r\)・\(e_θ\)を直交する大きさ\(1\)のベクトルなので、

\(e_r\)と\(e_r\)の内積は\(1\)
\(e_θ\)と\(e_θ\)の内積も\(1\)
\(e_r\)と\(e_θ\)は直交しているので内積\(0\)

という関係を使っています。

次に、\(er\)が定ベクトルではないので、これを\(r\)と\(θ\)で微分するということを考えるのですが、つまりこの式、

\(e_r = cos \ θ \ e_x + sin \ θ \ e_y\)
\(e_θ=-sin \ θ \ e_x + cos \ θ \ e_y\)

これを\(r\)と\(θ\)で微分してやればいいわけです。そうすると、この関数には\(r\)はどこにも入ってないので、\(e_r\)も\(e_θ\)も\(r\)で微分したものは\(0\)になります。

\(e_r・e_r = e_θ・e_θ = 1\)
\(e_r・e_θ = 0\)
\(\frac{∂e_r}{∂_r}=0\)

θで微分したものは\(cos \ θ\)と\(sin \ θ\)で微分すればいい、ということになります。

で、\(e_x\)と\(e_y\)は定ベクトル、乗数と同じことですので、そのまま乗数で残ります。これを計算すると、

\(\frac{∂er}{∂θ}= -sin \ θ \ e_x +cos \ θ \ e_y = e_θ\)

このようになり、答えは\(e_θ\)になります。そして\(\frac{∂e_θ}{∂_θ}\)はこのように計算できます。

\(\frac{∂e_θ}{∂_θ}=-cos \ θ \ e_x – sin \ θ \ e_y = -e_r\)

このようなものを、計算のパーツとして随所で使っていきます。

極座標での微分演算子

微分演算∇を計算していきます。∇は直交座標で表すと、

\(∇= \frac{∂}{∂_x}e_x+\frac{∂}{∂_y}e_y\)

このような形に表せるわけですから、これを\(rθ\)に変換していきます。

まずこの偏微分の公式を使って\(\frac{∂}{∂x}\)を変換してみると、上の式の\(\frac{∂}{∂_x}\)と\(\frac{∂}{∂_y}\)のところが、次のような関係になります。

\(=(\frac{∂}{∂r}\frac{∂r}{∂x}+\frac{∂}{∂θ}\frac{∂θ}{∂x})(cos \ θ \ e_r – sin \ θ \ e_θ)+(\frac{∂}{∂r}\frac{∂r}{∂y}+\frac{∂}{∂θ}\frac{∂θ}{∂y})(sin \ θ \ e_r +cos \ θ \ e_θ)\)

\(e_x \)と\(\ e_y\)はこのように書き換えられたわけですから、まずこのように計算することができます。

それから、さきほどの計算結果（下記）を、随所に代入していって計算します。

\(\frac{∂r}{∂x}=cos \ θ\)
\(\frac{∂r}{∂y}=sin \ θ\)
\(\frac{∂θ}{∂x}=-\frac{sin \ θ}{r}\)
\(\frac{∂θ}{∂y}=\frac{cos \ θ}{r}\)

そうすると、各々次のように計算できます。

\(=\{ cos \ θ \frac{∂}{∂r} + ( – \frac{sin \ θ}{r})\frac{∂}{∂θ} \}(cos \ θ \ e_r – sin \ θ \ e_θ) \)

\(+ ( sin \ θ \frac{∂}{∂r}+\frac{cos \ θ}{r} \frac{∂}{∂θ}) ( sin \ θ \  e_r + cos \ θ \ e_θ)\)

その結果、∇の演算子は

\(=\frac{∂}{∂r}e_r + \frac{1}{r}\frac{∂}{∂θ}e_θ\)

と表せます、ということになるわけです。

これを使っていくので、これを出したかったための計算でした。

🔵∇\(f\)（傾き）の計算

スカラー値\(f\)の傾きを考えますが、これは\(f\) に∇を左から演算するわけですので、これは単純に次のようになります。

\(∇f =( \frac{∂}{∂r}e_r+\frac{1}{r}\frac{∂}{∂θ}e_θ)f\)

そして\(f\)はスカラーなので、そのまま次のように計算できる、ということになるわけです。

\(=\frac{∂f}{∂_r}e_r+\frac{1}{r}\frac{∂f}{∂θ}e_θ\)

これを後で使っていくことになります。

電気双極子

さて、本題に入ります。

🔵電子双極子（Electric dipole）：等量、異符号の電荷が接近しておかれたもの

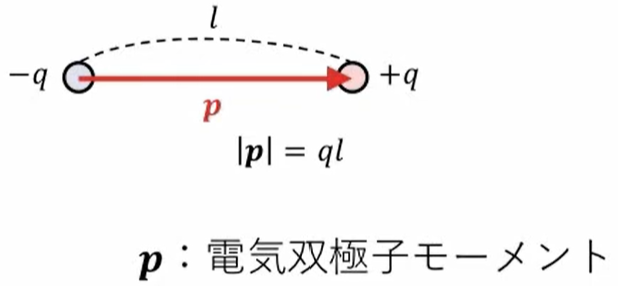
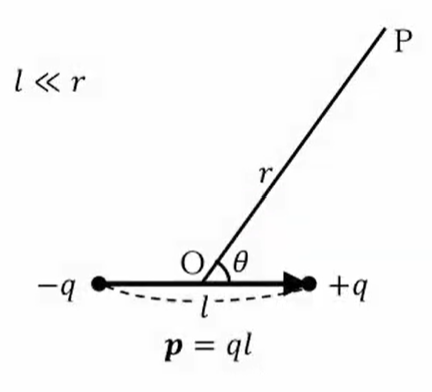
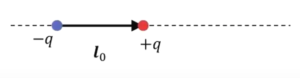
まず 「電気双極子」というものを考えます。「dipole」といいますが、これは等量で異符号の電荷が非常に近い距離（この場合は\(l\)）を離しておかれたもの、\(-q\)と\(+q\)、このことを「電気双極子」というふうに呼んでいます。で、これをベクトルで表して、ベクトルの向きを\(-q\)から\(+q\)に向かう方、マイナスからプラスの方向に取ります。

\(p\)の大きさ：この電荷\(q\)と\(l\)をかけたもの
向き：マイナスからプラスに向かう方向

このように「電気双極子モーメント」というベクトルを定義します。

電気双極子による電位、電場

ではまず最初に、「この電気双極子による電位と電場がどうなるのですか？」というのを計算するのですが、

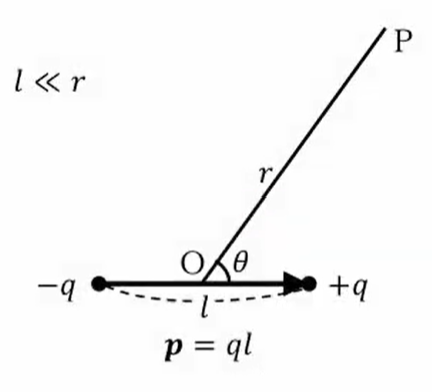
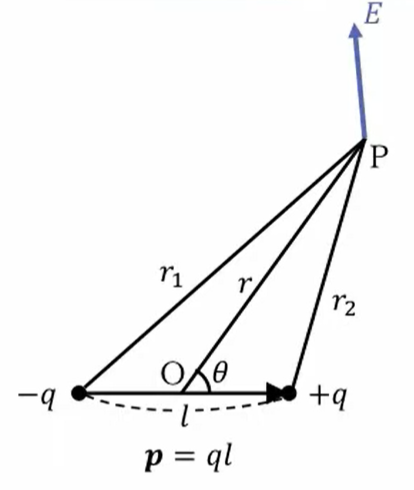
この\(-q\)と\(+q\)のところでの中心を原点\(O\)とおき、極座標\(θ\)を\(r\)で表します。その時\(p\)点の電位を計算するわけですが、さっき言ったように\(-q\)と\(+q\)は非常に接近しておかれているので、「考えている\(r\)に比べて\(l\)は非常に小さい」ということを想定します。そうすると、\(+q\)による電場と\(-q\)による電場を2つを重ね合わせればいいわけです。\(+q\)からの距離は\(r1\)、\(-q\)からの距離は\(r2\)になりますので、電位はこれの足し算ということで、次のように式に書くことができます。

\(V=\frac{q}{4πε_0r_1}-\frac{q}{4πε_0r_2}=\frac{q}{4πε_0}(\frac{1}{r_1}-\frac{1}{r_2})\)

この\(r1\)を\(r\)と\(θ\)で表すわけですが、次に書いた青のところ、三角形に余弦定理を適用しますと\(r1\)は下記の式のように表せます。

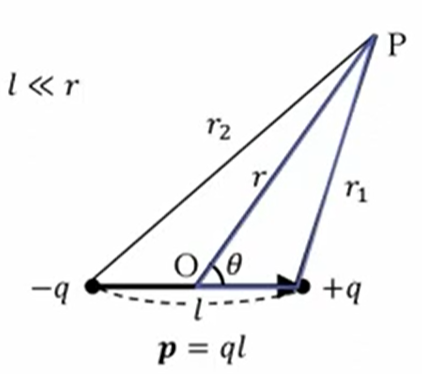
\(=\frac{q}{4πε_0} \{ \frac{1}{\sqrt{r^2+(\frac{l}{2})^2}-2r\frac{l}{2} cos \ θ} \}\)

で\(r2\)の方は、次の緑で書いた三角形に余弦定理を計算して適用すれば計算できます。

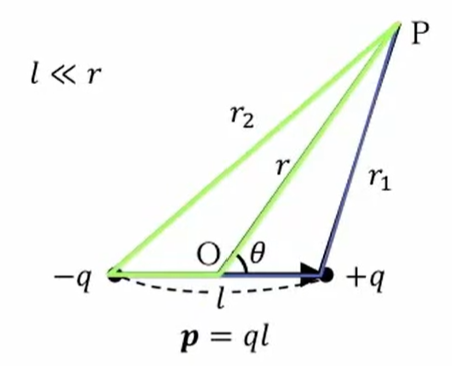
\(=\frac{q}{4πε_0} \{ \frac{1}{\sqrt{r^2+(\frac{l}{2})^2}-2r\frac{l}{2} cos \ θ} \ – \frac{1}{\sqrt{r^2+ ( \frac{l}{2})^2 – 2r \frac{l}{2} cos (π-θ)}}\}\)

\(=\frac{q}{4πε_0} \{ \frac{1}{\sqrt{r^2+(\frac{l}{2})^2}-rl \ cos \ θ}  – \frac{1}{\sqrt{r^2+ ( \frac{l}{2})^2 – rl \ cos (θ)}}\}\)

cos π-θは、-cosθですので、このような形になります。あとはこれを計算していくだけなんですが、あとはこれを計算していくだけなんですが、まず、ルートが分母にかかってきますので、これを指数表示して\(-\frac{1}{2}\)乗という形に書いておきます。

\(=\frac{q}{4πε_0} \{ (r^2+(\frac{l}{2})^2 – rl \ cos \ θ)^{-\frac{1}{2}} – ( r^2+ (\frac{l}{2})^2+rl \ cos \ θ)^{-\frac{1}{2}} \}\)

ここで\(r\)を前にくくりだして変形すると次のような形になります。

\(=\frac{q}{4πε_0r} \{ (1+\frac{1}{4} ( \frac{l}{r})^2 – \frac{l}{r} cos \ θ )^{-\frac{1}{2}} – (1+\frac{1}{4} (\frac{l}{r})^2+\frac{l}{r}  cos \ θ)^{-\frac{1}{2}} \} \)

\(l\)が\(r\)より非常に小さいわけですから、\(\frac{l}{r}\)というのは非常に微小な量になります。なので、まず2乗の方を無視してしまいます。

\(=\frac{q}{4πε_0r} \{ (1- \frac{l}{r} cos \ θ)^{-\frac{1}{2}} – (1+ \frac{l}{r} cos \ θ)^{-\frac{1}{2}} \} \)

このような形になります。

\(=\frac{q}{4πε_0r} \{ (1+ \frac{l}{2r} cos \ θ) – (1\frac{l}{2r} cos \ θ) \} \)

で、ここで物理学でよく使う近似式、 \(x\)が非常に小さいとき1より小さい時は\(1 +x\)の\(α\)乗は\(1+αx\)と記述できます。

\((1+x)^a≒1+ax　\ \ \ (x«1)\)

という近似を使って計算すると\(V\)がこのように計算できるわけです。

\(= \frac{ql \ cos \ θ}{4πε_0r^2}\)

で、\(\frac{p \ cos \ θ}{4πε_0r^2}\)になるんですが、\(p・r\)の内積であると、このような形になります。

\(= \frac{p \ cos \ θ}{4πε_0r^2}=\frac{p・r}{4πε_0r^3}\)

これが電気双極子によって点\(P\)に作られる電位ということになります。

じゃあ、電位が計算できればそれを微分することによって電場が計算できるわけですが、先ほどやったように原因は計算でき、\(rθ\)の関数として表すことができました。

\(V = \frac{p \ cos \ θ}{4πε_0r^2}\)

\(E = -∇V\)

電位はこの傾きを取ればいいわけですが、今は極座標で表しているので、先ほどやったように∇はこのような形になります。

\(E = -∇V = – \frac{∂V}{∂r}e_r – \frac{1}{r}\frac{∂V}{∂θ}e_θ\)

これを計算していけばいいわけです。\(r\)方向の成分は\(- \frac{∂V}{∂r}\)を計算すればいいわけですから、単純にこれを\(r\)で微分すればいいということで、このような形で計算できます。

\(E_r = -\frac{∂V}{∂r} = \frac{p}{2πε_0r^3} cos \ θ\)

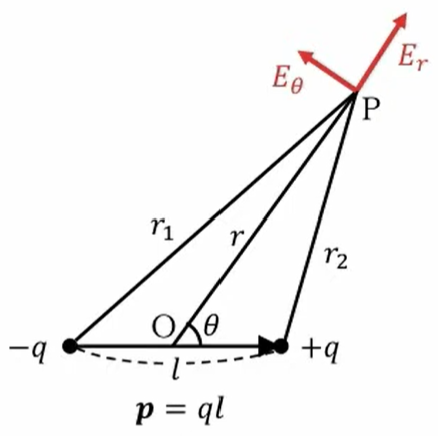
\(θ\)方向の成分は\({∂V}{∂θ}\)ではなくて、\(\frac{1}{r}\)が極座標にかかってきますので、このような計算をすれば\(E_θ\)が求まるわけです。

\(E_θ = -\frac{1}{r} \frac{∂V}{∂θ} = \frac{p}{4πε_0r^3} sin \ θ \)

微分するとこんな形で表せます。

すると、\(e_r\)と\(e_θ\)方向は極座標の基底ベクトルの方向を互いに持っているので、これを足し算してやると、実際の電場の方向になります。

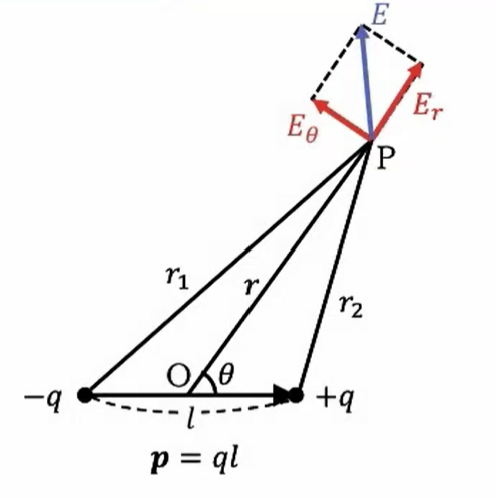
で、大きさは三平方の定理を使い、このような形で計算できます。

\(E = \sqrt{{E_r}^2+{E_θ}^2} = \frac{p \sqrt{1+3 \ cos^2 \ θ}}{4πε_0r^3}\)

これが電気双極子によって作られる電場です。

電気二重層

次に、似たようなもので「電気二重層」があります。

🔵電気二重層（Electric double layer, EDL） ■面密度が等しく、正電荷が一方の面、負電荷が他方の面に分布した、薄い層 ◆互いに接触した異種物質 ◆解質溶液に浸した正（負）の電位とした電極

ここに書いているように、綿密度が等しくて正電荷が一方の面、負電荷が他方の面に分布した、非常に薄い層のことをいいます。

最近、この「電気二重層コンデンサー」というのが市販されて使われているわけですが、非常に容量が大きいコンデンサーとして使われています。

では、「こういう状況がどのようなところで起こるのか」というと、互いに接触した異種物質のところ、片方がプラスを持ってマイナスを持っているとき、あるいは電解質溶液に浸した電極のところ、このところにも電極と反対側のイオンが溶液中で寄ってくるので、非常に薄いのが、プラスのもマイナスのもできるということです。

これが、具体的な電気二重層の例になります。

電気二重層による電位

この電気二重層による\(P\)点の電場、電位を計算していくことになるわけです。

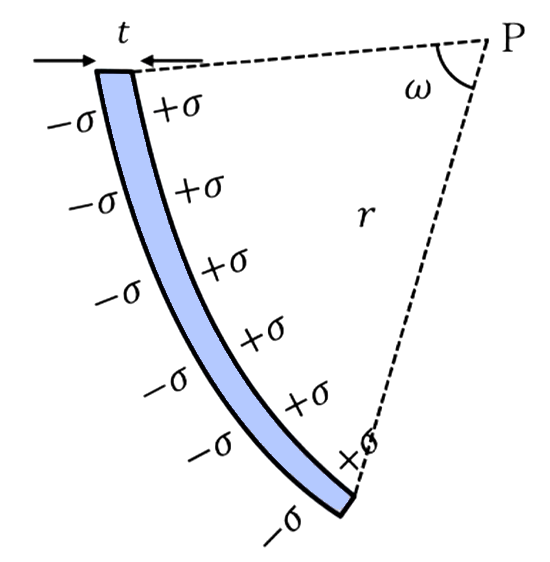
ここで書いてある\(Ω\)は、これは立体角です。これを計算していきます。

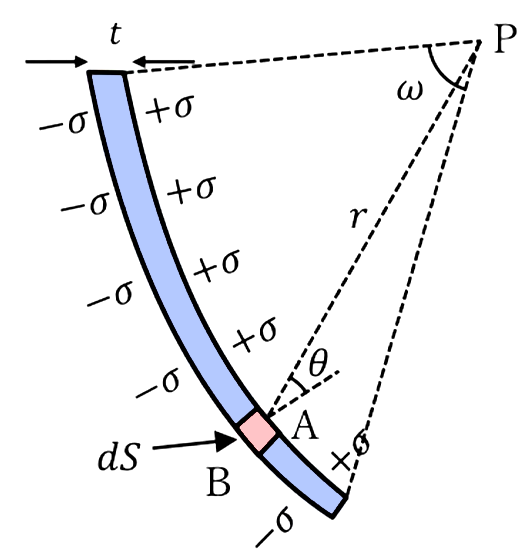
図形の赤い部分、微小なところの領域（\(ds\)）を考えますと、青いところが先程説明した双極子になってるわけです。

で、どのような双極子かというと、距離が\(t\)で電荷が\(σds\)という双極子になってる。

そうすると、それによる電場は先ほど計算しましたように計算しましたので、それを使いますと、この微小な領域による電波はこのような表せると。

\(dV = \frac{tσdS \ cos \ θ}{4πε_0r^2}\)

そうすると、この立体角、これを見込む立体角で表してあげますと、立体角はこのように微小立体角をこのように定義できますので、

\(±dω= \frac{dS \ cos \ θ}{4πε_0r^2}\)

これをまず用いてこれを変換してあげると、このような形に微小立体角で表すことができます。

\(=±\frac{tσ}{4πε_0}dω\)

\(±\)の符号が付いているのは、この場合は立体角はプラス側にある場合は正と定義しましょう、でこっちが逆にこっち側にある場合は、ここの時の立体角をマイナスと定義しましょうということで、プラスマイナスをつけてます。

立体角
＋：Ｐが＋側
ー：Ｐがー側

なので、これでこの微小なところにある双極子による電位が計算できたわけですから、これを全部で積分してやればいいわけでございまして、

\(= ±\frac{r}{4πε_0}dω\)
\(t=σt\) 　単位面積当たりの双極子モーメント

\(V\)は\(dV\)を計算して呼ばれるわけでありまして、これを積分するとこのような形で、非常にシンプルな形で立体角を用いると、シンプルな形に表せることになります。

\(V= \int dV = \int ±\frac{r}{4πε_0}dω=±\frac{r}{4πε_0}ω\)

 

電気二重層の表裏の電位差

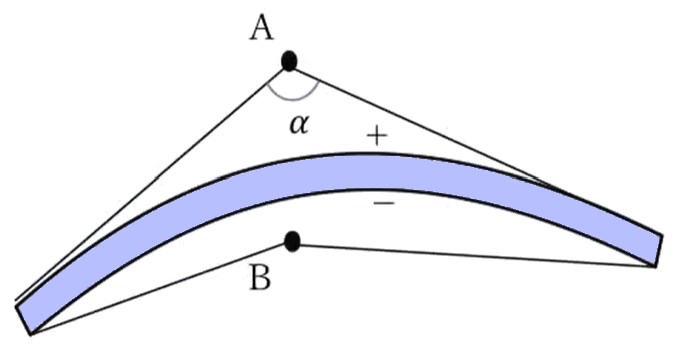\(V_A = \frac{τ}{4πε_0} α\)

で、それから「裏側と表側の電位差がどうなるの？」という話なんですが、先ほどあったように、\(Ａ\)がプラス側にある方の立体角を\(α\)て考えますと、\(A\)点の電位はこのように表されたわけです。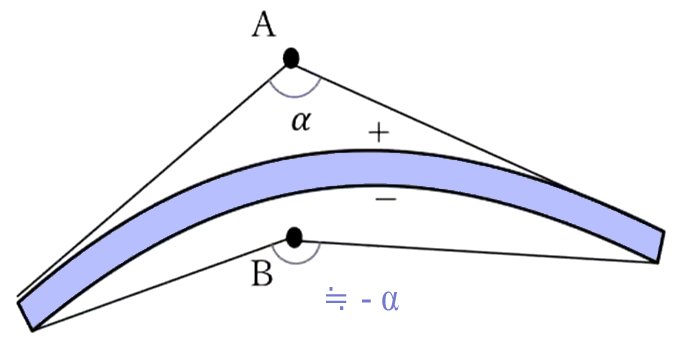

じゃあ裏側の電位は、非常にこれが近いとここの角度っていうの はαとほぼ同じになりますが、マイナス側にあるので、先程言ったようにこの角度はマイナスをつけておきます。

で、そうすると、これを見込む立体角は全体からこの部分を引いたものになります。

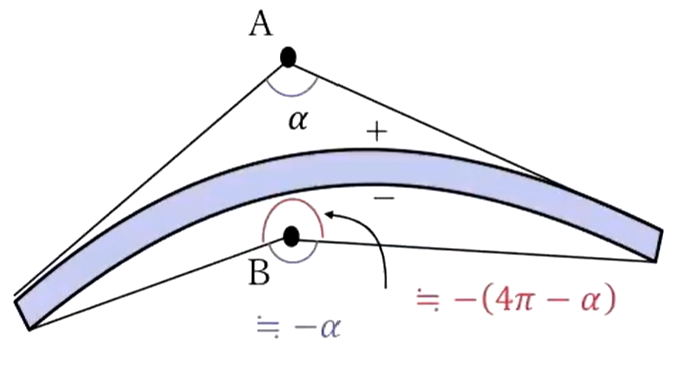
で、全方位を見渡した立体角は\(4π\)なので、\(4π\)から\(α\)を引いたもの、なのでこれがB点の電位になりまして\(V_B\)点の原因がこのように計算できます。

\(V_B=\frac{τ}{4πε_0} \{ -(4π – α) \} \)

そして\(A\)点と\(B\)点の電位差を計算しますと、これを引き算してやればいいわけでして、単純に非常にこれもシンプルです。

\(V_{AB}=V_A-V_B = \frac{τ}{4πε_0}4π=\frac{τ}{ε_0}\)

裏側と表側の電位差は\(ε_0\)分の\(τ\)（タウ）、タウというのは\(σt\)です。厚さを今「面密度を\(t\)」と考えていますので、このような電位差になります。これが、電気二重層による電位差の話です。

 

例題

では、例題をやっていきます。

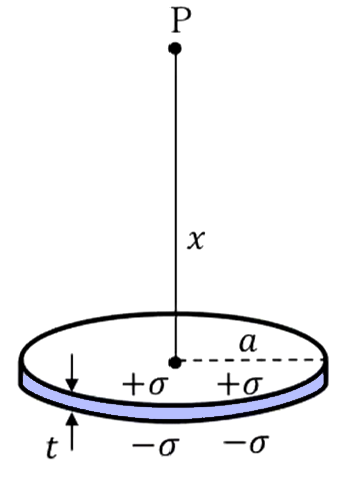
半径\(α\)、厚さ\(t\)の円板が、表裏に一様な面密度\(±σ\)で帯電しているとき、円板の中心軸の板から正電極側に距離\(x\)の点\(P\)での電位と電場を求めよ。

これは非常に薄い円盤の電気二重層になっているわけでして、まず立体角を計算すると、これ対照的ですので、

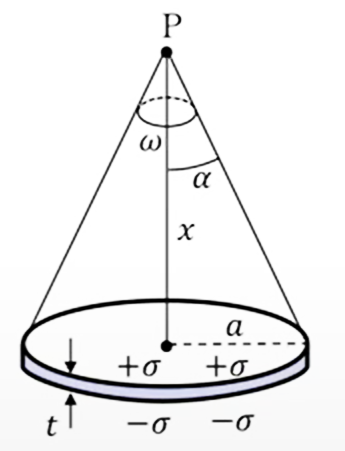
半頂角を\(α\)とすると\(Ω\)は先ほどから出ているように、\(2π (1-cosα)\)ということになります。で、\(cos α\)を以下の

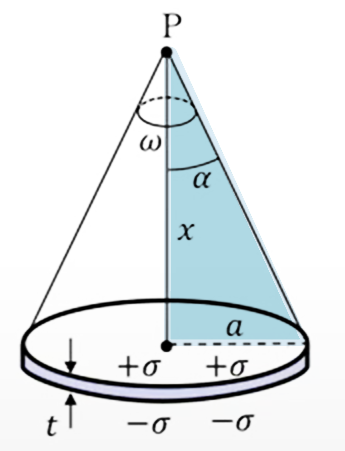
この直角三角形で書き直してやると、このような形に計算することができます。

\(ω = 2π (1 – cos \ α ) = 2π (1- \frac{x}{\sqrt{x^2+α^2}})\)

で、そうすると、電位は\(\frac{σt}{4πε_0}ω\)の立体角と表せたわけですから、立体角の\(ω\)にこの上の式を代入してやると、\(V\)を\(x\)の関数として表すことができます。

\(V=\frac{σt}{4πε_0}ω=\frac{σt}{2ε_0}(1- \frac{x}{\sqrt{x^2+a^2}})\)

そうすると、もうこれは電場は単純に電位を微分すればいいわけですから、\(E=-\frac{∂V}{∂x}\)を\(x\)で微分してやると、このように計算できます。

\(E=-\frac{∂V}{∂x} =\frac{σt}{2ε_0}\frac{a^2}{(x^2+a^2)^{\frac{3}{2}} } \)

これが円板状の電気二重層による、電場と電位の例題になります。

 

電気多重極子

さて、先ほどは\(+q\)と\(-q\)の2つの電荷がある、いわゆる双極子というのを考えたのですが、一般にこれをずっと展開していって多重極子というのが考えられます。一般に考えられるのは2の2重極子なので、考えられるのは2重極子、4重極子、6重極子、8重極子、16重極子という2のN乗倍になります。多重極子のことを次のように言っていました。

🔵\(2^n\)重極子：\(p^{(n)}\)

で、これをどのように定義するかというと、それの1個前の多重極子、\(2^n\)重極子は、\(2^{n-1}\)重極子と、それと逆符号にした多重極子を持ってきて、その多重極子をある方向に変異させる、というふうに考えます。

■\(2^{n-1}\)重極子とその逆符号のものを\(l_{n-1}\)変位

これはわかりにくいので、具体的に図で説明したいと思いますが、その後でその多重極子の大きさを有限にしたまま距離を非常に小さくしていくという作業をとります。

で、n重極子のモーメントは、「\(n\)と\(p^{(n)}\)に変異した距離をかけたもの」というふうに定義します。

■モーメント：\(p^{(n)}=np^{(n-1)}l_{n-1}\)

で、\(p^{(0)}\)の場合は、この場合は、単に点電荷があるだけ、というふうに考えます。

■\(p^{(o)}=q\)（点電荷）

多重極子は非常にわかりづらいので、具体的に見ていきたいと思います。

まず\(n=1\)の場合です。2の\(n\)乗の場合で、2の\(n\)重極子ということです。これは\(p^{(1)}\)で表すわけですが、これは先ほどやったように双極子ということになりますので、そのままです。

🔵\(n=1\)：2重極子（双極子）：\(p^{(1)}\)
■\(2^0\)重極子（点電荷）

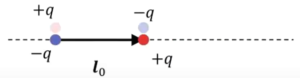
同じように、ここにまず\(-q\)というものを考えると、その1個前なので、\(p^{(0)}\)、点電荷を考えるわけです。最初に\(-q\)を考えると、それと反対符号の点電荷を持ってきますよと。

で、これを\(l_0\)動かします。

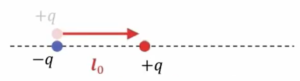
そうするとこのようになって、

これが\(p\)の双極子ということになります。

■モーメント：\(p^{(1)}=1p^{(0)}l_0=ql_0\)

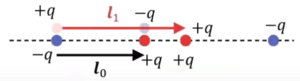
で、次に\(n=2\)の場合、4重極子ですが、40重極子なのでその1つ前の2重極子、双極子を考えます。

🔵\(n=2\)：4重極子：\(p^{(2)}\)
■\(2^{1}\)極子（双極子）

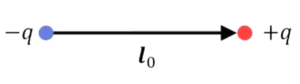
この双極子でこれと逆符号のものをまずポンと置いてあげます。

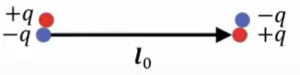
で、これをある方向に、\(l_1\)方向に変位させます。

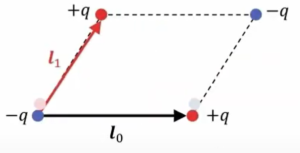
■\(2^{1}\)極子（双極子）とその逆符号のものを\(l_1\)変位

これが、一つの4重極子の例になります。

でこれは、\(l_0\)と\(l_1\)と方向を、別の角度の方向に動かしたわけですが、同じ方向に動かすことも可能です。

■モーメント：\(p^{(2)}=2p^{(1)}l_1=2・1ql_0l_1\)

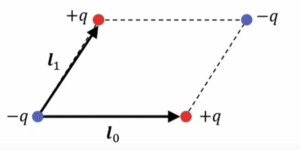
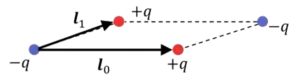
これもやっぱり双極子を考えて、逆向きの双極子を考えて、

これを右側にずらしてやると、

このような形になって、4つの電荷が並ぶわけですが、これも4重極子の1部です。

で、次に\(n=3\)ぐらいまでは図にかけますが、それ以上書くのは難しいですが、まず8重極子です。\(n=3\)を考えます。

🔵\(n=3：8\)重極子：\(p^{(3)}\)
■\(2^2\)重極子（4重極子）とその逆符号のもの

なので、その1個前の\(p=2\)、2の2重極子、つまりまず4重極子を考えます。

で、それと反対符号のものを持ってくるのでしたから、これの符号を全部入れ替えたものを考えます。

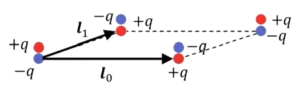
これを、ある変位\(l2\)方向にポンと動かします。だから、電荷が8個あります。

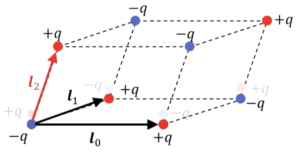
結果的にこれが8重極子の1つの例になります。

で、この後ずっと考えられていくのですが、これ以上はちょっと絵に書くのは難しいので、これぐらいのところでやめておきますが、これを電気多重極子と言います。

多重極子（\(2^n\)重極子）による電位

では次に、多重極子\(2^n\)重極子による電位、ということを考えていきます。

そうすると、まず定義として、ここに赤で囲った\(p^{(n)}\)重極子があると考えるわけですが、

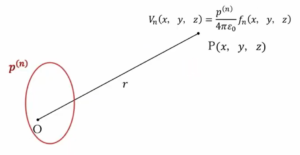
これから距離\(r\)離れたところの点電位を考えます。で、これを\(n\)重極子による電荷ということで\(Ｖ_n\)というふうにするわけですが、これを必ず\(\frac{p^{(n)}}{4πε_0}\)というのが入ってくるので、\(4πε\)の\(p^{(n)}\)と\(rxyz\)における関数\(f_nx\)で表せますよ、というふうに定義しておきます。

\(V_{n+1}(x,y,z)=\frac{p^{(n)}}{4πε_0}f_{n+1}(x,y,z)\)
\(P(x,y,z)\)

そうすると、\(V_{n+1}\)を考えるわけですが、\(V_{n+1}\)はこのように\(\frac{p^{(n+1)}}{4πε}\)の\(FのN+1XYZってことになるわけです。

\(V_{n+1}(x,y,z)=\frac{p^{(n+1)}}{4πε_0}f_{n+1}(x,y,z)\)

そうすると\(n+1\)重極子はその前の双極子、\(p^{(n)}\)重極子をある変位\(l_n\)を符号を変えて動かしたものですので、符号が違うのが元あった「\(fn(x)\)」)です。

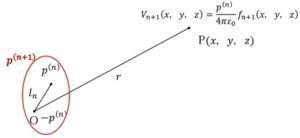
\(V_{n+1}(x,y,z)=\frac{p^{(n+1)}}{4πε_0}f_{n+1}(x,y,z)\)
\(=\frac{p^{(n)}}{4πε_0}[f_n(x-α_nl_n, y-β_nl_n, z-γ_nl_n)-f_n(x,y,z)]\)

で、符号をかけて\(ln\)だけ動かします。で、上記の\(α_n\)、\(β_n\)、\(γ_n\)、これは方向余弦です。

つまり、直交座標\((x, y, z)\)で考えますと、

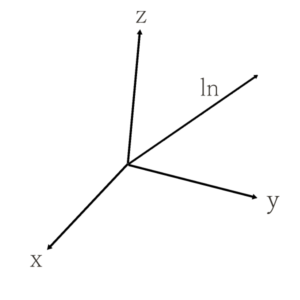
ある変位させた\(l_n\)というベクトルを考えるわけですが、これと\(x\)軸のなす角度のcosがある場合、

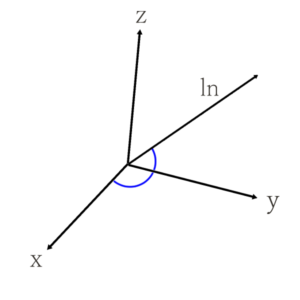
\(y\)軸との角度のcosを取ったものが\(β_n\)、

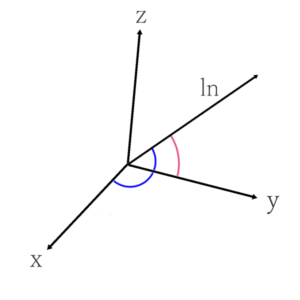
このベクトルと\(z\)軸のcosを取ったものが\(γ_n\)です。

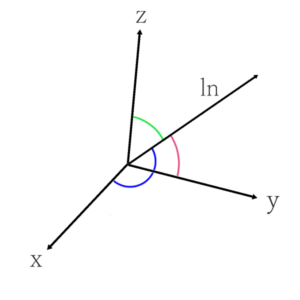
そうすると、ここで書いてあるのは、\(ln\)による\(x\)方向への変化量、\(y\)方向の変化量になるわけですから、このように表すことができます。

でこれを計算していくわけですが、そうするとこれは引き算で、よくあるように二次以降の近似、一次近似を取ってしまいます。

\(V_{n+1}(x,y,z)=\frac{p^{(n+1)}}{4πε_0}f_{n+1}(x,y,z)\)
\(=\frac{p^{(n)}}{4πε_0}[f_n(x-α_nl_n, y-β_nl_n, z-γ_nl_n)-f_n(x,y,z)]\)
\(=\frac{-p^{(n)}l_n}{4πε_0}(α_n\frac{∂f_n}{∂x}+β_n\frac{∂f_n}{∂y}+γ_n\frac{∂f_n}{∂_z})+\)（\(l_n\)の2次以上の項）

このように微分で表すことができるわけです。1次元で書くとこういうことと同じなのですが、

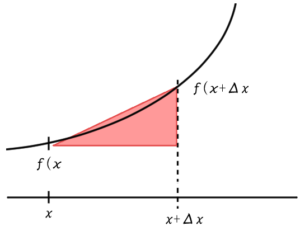
この値を直線で定義してるわけです。で、それを3次元でやって、展開したやつです。ある意味で3次元のテイラー展開ということもできるんですが、それをやってる、一次近似しているということになります。

で、これで計算していくわけですが、

3行目の式中盤の\((α_n\frac{∂f_n}{∂x}+β_n\frac{∂f_n}{∂y}+γ_n\frac{∂f_n}{∂_z})\)の部分を、次のように定義できます。

\(\frac{∂f_n}{∂l_n}\)

そして、\(p^{(n+1)}\)重極子は、その1つ前の\(n\)重極子を表して、

\(p^{(n+1)}=(n+1)p^{(n)}\)

このような形に表せるわけでしたので、これを使って計算してみます。\(V_{n+1}\)はこのように計算できます。

\(V_{n+1}=-\frac{1}{4πε_0}\frac{p^{(n+1)}}{n+1}\frac{∂f_n}{∂l_n}\)

そうすると、\(\frac{1}{4πε_0}\)の\(p^{(n+1)}\)で、その他の部分を関数\(f\)と置いたわけですので、この場合の\(f_{n+1}\)は次のような形になります。

\(f_{n+1}=-\frac{1}{n+1}\frac{∂f_n}{∂l_n}\)

で、これを順次計算していくんですが、まず\(V_0\)というのを計算します。\(V_0\)というのは点電荷による電位なので、単純に前回の第2回でやったように、点電荷による電荷になります。この場合の\(P_0\)は点電荷なので\(q\)、\(f_0\)はこの場合は\(\frac{1}{r}\)です。

\(V_0=\frac{1}{4πε_0}\frac{q}{r}\)
\(p^{(0)}=q\)
\(f_0=\frac{1}{r}\)

で、これを使って、これ漸化式みたいな形になっているので\(V_{n+1}\)が\(f_n\)と\(l_n\)で表されているので、これを順次計算していきます。\(V_1\)はこれを\(P\)値と置いて\(l_0\)で微分したものということになります。なので、この形(\(V_{n+1}(x,y,z)=\frac{p^{(n+1)}}{4πε_0}f_{n+1}(x,y,z)\))で表せるようにしてやると、

\(V_1 = -\frac{1}{4πε_0} \frac{p^{(1)}}{1} \frac{∂f_0}{∂l_0} = -\frac{p^{(1)}}{4πε_0} \frac{∂}{∂l_0} (\frac{1}{r}) \)

という形になり、この場合の\(f_1\)というのは、

\(f_1=-\frac{∂}{∂l_0}(\frac{1}{r})\)

このような形で、\(\frac{1}{r}\)を変位方向で微分してやるもの、ということになります。

で、同じように\(V_2\)も計算するには、\(V_1\)をさらに計算してやればいいので、

\(V_2 = -\frac{1}{4πε_0} \frac{p^{(2)}}{2} \frac{∂f_1}{∂l_1} = \frac{1}{4πε_0} \frac{p^{(2)}}{2!} \frac{∂^2}{∂l_0∂l_1}(\frac{1}{r})\)

\(f_2=\frac{1}{2!} \frac{∂^2}{∂l_0∂l_1} (\frac{1}{r})\)

このような形に表すことができるわけです。

これを繰り返しずっと行なっていくと、\(n\)番目は次のような形に表せる、ということなんです。

\(V_n= \frac{(-1)^n}{4πε_0} \frac{p^{(n)}}{n!}\frac{∂^n}{∂l_0∂l_1…∂l_{n-1}} (\frac{1}{r})\)

\(f_n = \frac{(-1)^n}{n!} \frac{∂^n}{∂l_0∂l_1…∂l_{n-1}}(\frac{1}{r})\)

これが\(p\)のn重極子（\(p^{n}\)）による電位、つまり\(2^n\)重極子による電位、ということになります。

電位の多重極展開

次に、電位の多重局展開というのがあります。それがどういうことなのか、というのをまず書いておきます。

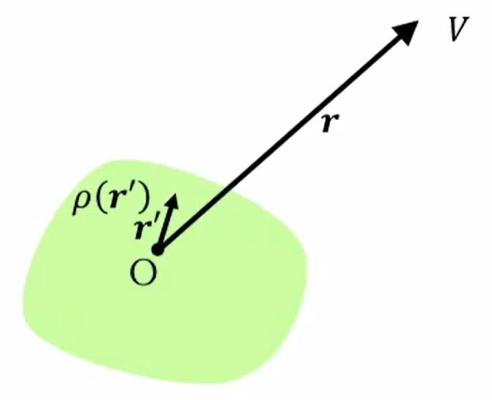
多重極子に\(p^n\)重極子、つまり\(2^2\)重極子による電位は、先ほど書いたのと同じですが、

\(V_n= \frac{(-1)^n}{4πε_0} \frac{p^{(n)}}{n!} \frac{∂^n}{∂l_0∂l_1…∂l_{n-1}} (\frac{1}{r})\)

このように計算することができたわけです。で、図のグリーンに書いた部分、一様ではなくて、任意の形に電荷が分布していると。で、これから離れた点の電位がどうなるかということです。

結論から言うと、この電位はさっき言った多重極子の重ね合わせとして表すことができる、というのが「電位の多重極展開」ということになります。

なので これは\(n\)重極子なので、全ての多重極子による重ね合わせと考えます。これを全部足し算して割ればいいので、次のように\(∑\)を取ってやればいいという形になります。

\(V=\displaystyle \sum_{n=0}^{∞}V_n = \frac{1}{4πε_0} \displaystyle \sum_{n=0}^{∞}\frac{(-1)^np^{(n)}}{n!}\begin{bmatrix}\frac{∂^n}{∂l_0∂l_1…∂l_{n-1}}(\frac{1}{r})\end{bmatrix}\)

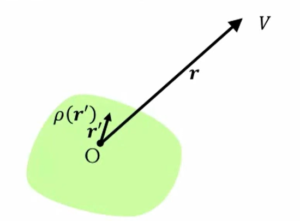\(V=\frac{1}{4πε_0}\int \frac{ρ(r’)}{r} dv’\)

一方、じゃあここの微小な円に電位が分布していた場合、ここの体積要素を考えて電位を計算してやればいいわけですが、これを計算していくと、先程のＦ\(V=\displaystyle \sum_{n=0}^{∞}V_n = \frac{1}{4πε_0} \displaystyle \sum_{n=0}^{∞}\frac{(-1)^np^{(n)}}{n!}\begin{bmatrix}\frac{∂^n}{∂l_0∂l_1…∂l_{n-1}}(\frac{1}{r})\end{bmatrix}\)の式とまったく同じになる、というのが定義です。

ここで少しハードな数学を使うので結論だけ述べて計算を省略しますが、具体的に何を計算するのかというと、\(\frac{1}{r}\)が入ってるので、\(\frac{1}{r}\)をテイラー展開して計算していけばこれを導くことができます。

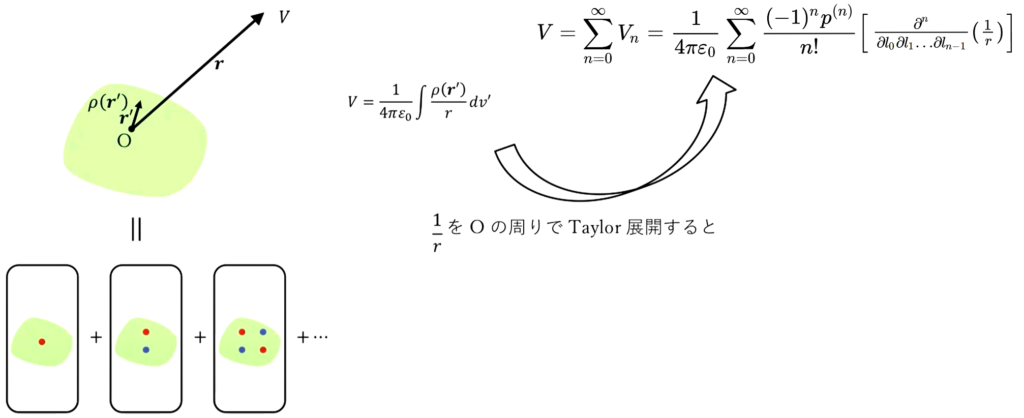
細かいことは省略しますが、ということはここに任意の点が分布した電位が\(V=\frac{1}{4πε_0}∫\frac{ρ(r’)}{r} dv’ \)のように表せます。で、これは多重極子を全部足し合わせた電位なんですよっていう話だったので、任意の電荷分布をもった領域からの電位というのは、多重極子を全部足し合わせることによって表現できますよ、というのが、この電位の多重局展開という話でございます。

で、ちょっと難しい話でこれも結論だけに行ってみますけど、これは直交座標で表したましたけど、今日やってませんけど3次元の曲座標というのがありましてこれで3次元教材票で表しますと。このような形に計算できることがわかってます。

ここに1つ、わけのわからない関数が入ってきてるんですが、これは実は球面調和関数と言われる関数で、具体的にはこのように計算できます。

難しいので結論だけにしますが、これは直交座標で表しましたが、今回やっていない3次元の極座標というものがありまして、3次元極座標で表すと、

\(V=\frac{1}{4πε_0} \displaystyle \sum_{n=0}^{∞} p^{(n)} \frac{Y_n(θ,φ)}{r^{n+1}} \)

このような形に計算できることがわかっています。で、またここに\(Y_n(θ,φ)\)という関数が入ってきているわけですが、これは球面調和関数という関数で、具体的には次のように計算ができます。

\(Y_n(θ,φ)=\displaystyle \sum_{m=0}^{n}(a_{nm} cos \ mφ + b_{nm} sin \ mφ)p_{n}^{m}(cosθ)\)

そこでまた、\(p_{n}^{m}(cosθ)\)という新たな関数が入っていますが、これは陪 Legendre関数という関数です。

\(p_{n}^{m}(x)=(1-x^2)^{m/2}\frac{d^mP_m(x)}{dx^m}\)

\((1-x^2)\frac{d^2y}{dx^2}-2x\frac{dy}{dx}+n(n+1)y=0\) の解

性質としてはこのような性質を持っていて、具体的にはこのような微分方程式の解として定義します。この微分方程式が解けないので、この解をこんな関数と置いてしまいましょうというやつです。

いわゆるこういうものを数学の分野で「超越関数」と呼んでるんですが、微分方程式が解けない、あるいは積分ができないから、それを関数としてするとして置いてしまいましょう、というものです。

代表的なのは物理学で使っていくものは、ベッセル関数などの色々な関数がありますが、全て超越関数と呼ばれているものです。

で、陪Legendre関数の\(\frac{d^mP_m(x)}{dx^m}\)でもまた新しく\(P_m\)が入ってきているので、これを展開してやります。

Legendre 関数　\(P_n(x)=\frac{1}{2^nn!} \frac{d^n(x^2-1)^n}{dx^n}\)

\((1-x^2)\frac{d^2y}{dx^2}-2x\frac{dy}{dx}+ \{ n(n+1)-\frac{m^2}{1-x^2} \} y=0\) の解

\(P_n(x)\)はルジャンドル関数です。これはルジャンドルという人が定義した数学者の人が定義したんですが、この人が、電位を考えるとき、\(\frac{1}{r}\)を多重極展開するときにどう表せますかっていうのを数学的に表したのがもともとの始まりなんですね。だから「数学のルジャンドル関数をここに適用している」のではなくて、「この電位の問題を解くため、にこのような関数を考えてきました」というのが結論です。計算は非常にで高度で、難しいというよりも長い計算になりますので、省略しますが、このような形に表せます。

実はこの球面調和関数というのは、ここでは電位の話をしていますが、物理学では色々なところで出てくる関数です。例えば、後で「ラプラスの方程式」を解くということをやるんですが、このラプラスの方程式は、球対称な場合にはこのような形で球面調和関数になります。後の具体的な例としては、量子力学で原子の量子状態を計算するときもそうです。原子は原子核を中心とした球対称な形を持っているので、そこで量子状態を計算する時も、この球面調和関数というのは出てきます。

あとは球面波、つまり波動です。ある一点から波がどんどん広がっていきますよという球面調和です。これを式で表そうとした時も球面調和関数になりますので、球対称とした時の方程式の解として出てくる時には、球面調和関数というのは物理学では頻繁に出てくる関数ではあります。この場合は電磁気学をやってますので、電位の多重極展開のところで球面調和関数を使います。

難しい式がいっぱい出ていますが、これは公式として覚えるようなものでもなくて、とても覚えられるものでもありません。大事なのは、先ほどの繰り返しですが「任意分布した電荷分布は、多重極子の重ね合わせとして表現することができますよ」ということを、定性的に理解しておくということです。

それからそれを計算すると、極座標で表すとこのような球面上は関数とかルジャンドル関数を使うと比較的がシンプルな形で表現することができますよ、っていうのを定性的に理解しとけばここのところではいいと思います。

計算は、興味がある人はやってほしいんですが、非常に計算量が多い計算になるため、ここでは省略します。

まとめ

今回は、双極子から始まって、電気多重極子というものを考えてきました。

いわゆる2重極子、4重極子、6重極子、8重極子、16重極子と、どんどんつながっていくわけですが、それによって電位がどんな形になるんですか、というのを考えました。そして、それを元にして任意の電荷分布を持ったところから距離\(r\)離れたところの電位は、多重極の重ね合わせとして表されるんですよ、ということを今回は述べました。

これが、電位の多重極展開としての場合です。正電場のところでは比較的重いところになるため、計算は一部省いて定性的理解というところに留めていますが、これが電位の多重極展開という話で、今回は終わります。

 

関連記事：【大学物理】電磁気学シリーズ

第1回 – 静電気、帯電、静電誘導、誘電分極 –
第2回-【大学物理】電磁気学 第2回① – Coulombの法則
第2回-【大学物理】電磁気学 第2回② – ベクトル解析の基礎（電場、電位に必要な数学）
第9回 – 静電容量(コンデンサー) –