【1】最適消費行動とは

われわれ消費者は限られた予算の範囲内で満足度が最も大きくなるように買物をします。これを「最適消費行動」といいます。今回は「最適消費行動」を「予算制約式」と「効用関数」を使って説明します。数式とグラフを使いますが、がんばってついてきてくださいね。

【2】予算制約式の基本

【3】XとYの購入量を求める

【4】予算線の意味

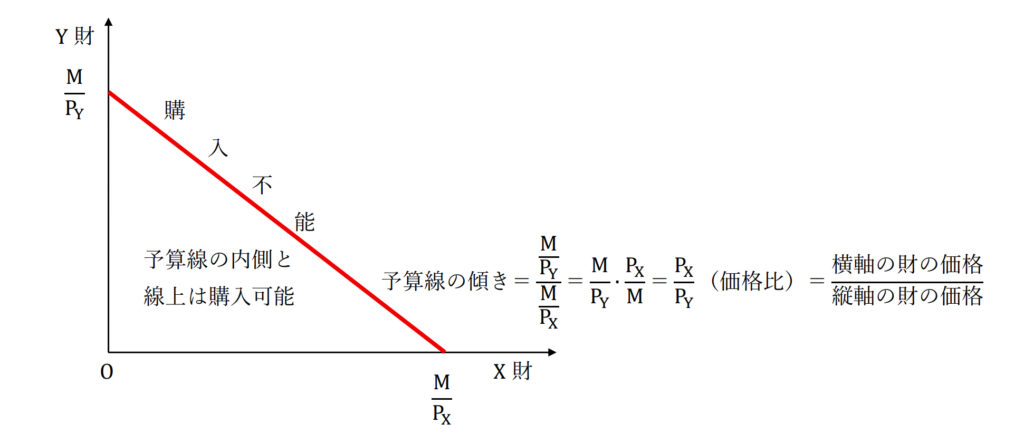
以上の関係をグラフにすると次のようになります。

Y＝０、X＝０という買い方は極端な買い方です。実際は二財の価格を見ながら、ほどよい買い方をします。赤色の直線が「予算線」です。この「予算線」が「購入可能領域」と「購入不能領域」の境界線となります。

今後の理解において、両軸の切片が非常に重要な意味を持ちますので、先ほどの導出過程をしっかりと理解してください。予算線の傾きが「価格比」になっていることも非常に重要です。価格比については別の機会に詳しく説明します。

【5】予算制約式の数値例

予算制約式に数値を入れてみましょう。

200＝10X＋10Y
とすれば
Y＝0のときX＝10、X＝０のときY＝10となります。

数値を入れると理解しやすくなりますが、理論的な説明を進めるときには文字式が威力を発揮しますので、文字式による表現に慣れてください。

【6】効用関数と無差別曲線

続いて、「効用関数」から「無差別曲線」を導出します。「無差別曲線」というと、何か得体が知れないものに聞こえますが、「無差別＝差がない＝同じ」という意味です。

財の購入において「満足度が等しくなる」二財の組み合わせを曲線で示したものを「無差別曲線」といいます。

効用関数：U＝X・Y

このように「効用関数は掛け算」で表現します。「掛け算」にするのはX≠0、Y≠0としてU≠0という意味を持たせているからです。つまり、両方の財を同時に購入（消費）するということです。

消費者にとって二財とも同じ程度に必要な財ですので、購入の際に合理的な判断（無駄な買い方をしない）を行うことが仮定されています。それでは次の段落で、無差別曲線を実際に書いてみましょう。

【7】無差別曲線の具体例

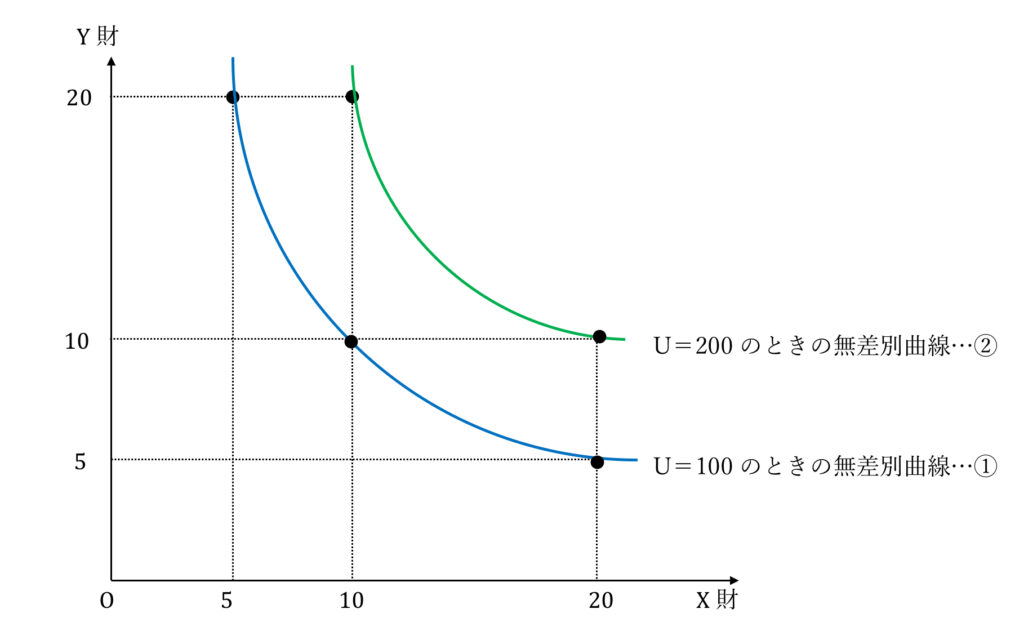
効用関数のUを100と仮定すると100＝XYとなり、X＝10のときにはY＝10、X＝5のときにはY＝20となり、どちらの組み合わせもU＝100であり同じ満足度（無差別）となります。

同様に、効用関数のUを200と仮定すると200＝XYとなり、X＝10のときにはY＝20、X＝20のときにはY＝10となり、どちらの組み合わせもU＝200であり同じ満足度（無差別）となります。

この図から満足度が大きい無差別曲線が上方にあることを確認してください。財の消費量の大きさが満足度（総効用）の大きさを示しています。単純に「たくさんあると嬉しい」ということです。

【8】おやつの例えで考える最適消費行動

子供のころに遠足に行くとき、リュックの大きさや決められた金額（予算）の範囲内で持っていく「おやつ」を一生懸命に考えた経験（合理的な判断）があると思います。

無差別曲線はリュックに入れる「おやつの組み合わせ」のようなものとイメージしてください。「予算の範囲内」でリュックに入れる「おやつの組み合わせ」を一生懸命に考えることを「最適消費行動」といいます。

実際はたくさんある「おやつ」を二種類に限定して説明しているものが「無差別曲線」なのです。

【次回予告】

次回は「最適消費点」を具体的に見ていきます。一緒にしっかり理解していきましょう！

執筆者プロフィール

S（イニシャル）
1964年生まれ。
公務員試験対策予備校や大学・専門学校など、様々な現場で学生を指導してきました。
得意なのは大学レベルの経済学、経営学、会計学で、究進塾では主に大学授業補習コース（オンライン）を担当。

長年の豊富な指導経験から、「学生のつまづくポイント」を的確に把握しています。
堅苦しい「経済学」という学問を丁寧に解きほぐし、わかりやすく説明します。
とても親しみやすい性格で、質問もしやすいです。
生徒様お一人お一人に合わせた、また基礎を大切にした丁寧な指導がモットーです。