こんにちは。究進塾 編集部です。

川崎医科大学附属高校の入試対策シリーズの3回目です。今回は、令和2年一般入試の「数学」第2問の解説をします。

第2問の内容

内容は、関数（1次、2次）と、簡単な図形の融合問題になっています。

問題

図のように、放物線\(y=ax^2 (a>0)\)…①上に点Aと点Bをとる。ただし、線分ABは\(x\)軸と平行である。このとき、次の（　　）や　　　の中にあてはまる数、または式を書き入れなさい。

以上が問題文で、問いは(1)～(5)まであります。

最初に問いを全部読むと忘れちゃうので、1つずつやっていきましょう。

 

(1) a = (　　) であり、Bの座標は（　　,　　　）である。

まず\(y = ax^2\)の「aの値を求めなさい」という、お約束の問題です。点Aがこの放物線上にあるわけですから、座標\((3,\frac{9}{2})\)が\(y=ax^2\)を満たしてます。なので、これを\(x、y\)それぞれ代入してaを求めればいいわけです。

Aは放物線上の点だから
\(\frac{9}{2}=a×3^2\)
\(a=\frac{1}{2}\)

aは\(\frac{1}{2}\)になります。

それからBの座標ですが、AとBは平行なので、放物線は\(y\)軸に対して対称です。

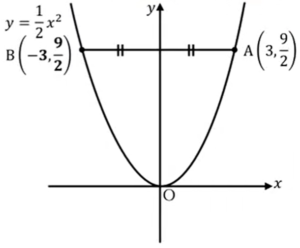
なのでBの座標は、\(y\)の座標はそのままで\(x\)の座標がプラスがマイナスになった-3。Bの座標は\((-3, \frac{9}{2})\)ということになります。

ABは\(x\)軸に平行だから、Bは\(y\)軸に対して対称
\(B=(-3,\frac{9}{2})\)

A.　 \(a=\frac{1}{2}\)　、\(B(-3,\frac{9}{2})\) 

 

(2)　△OABの面積は（　　）である。△OABを\(y\)軸を回転の軸としてできる回転体の体積は（　　）である。

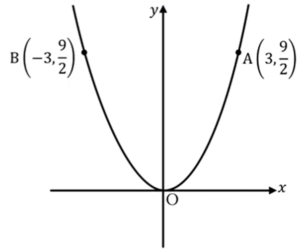
三角形はこういう三角形を求めればいいわけです。

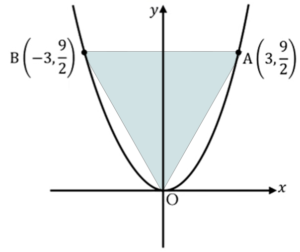
面積はABを底辺、\(y\)軸のところを高さとして求めることができます。底辺は-3から3つまり6、高さは\(\frac{9}{2}\)なので\(\frac{27}{2}\)でとなります。

△OABの面積は
\(\frac{1}{2}・6・\frac{9}{2}=\frac{27}{2}\)

 

次に、これを\(y\)軸を中心に回転させるわけですが、そうするとこのような円錐が出来上がります。

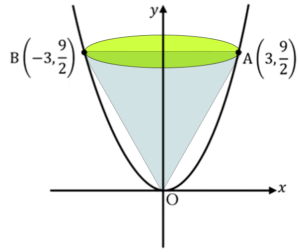
円錐なので\(\frac{1}{3}\)で、半径が3なので\(π3^2\)、これが底面積になります。

△OABの回転体は、底面がABを直径とする円の円錐、その体積は
\(\frac{1}{3}・π(3^2)・\frac{9}{2}=\frac{27}{2}π\)

A.　\(\frac{27}{2}\)、\(\frac{27}{2}π\)

 

(3)　点Cと点Dは放物線①上の点で、\(x\)座標がそれぞれ正、負とする。また、点Eと点Fは\(x\)軸上の点とする。このとき、四角形CDEFが正方形になるような点Cの座標は（　　,　　）である。さらに、四角形ACGBが平行四辺形になるような点Gの座標は（　　,　　）である。

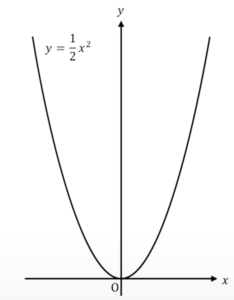
書き入れると、

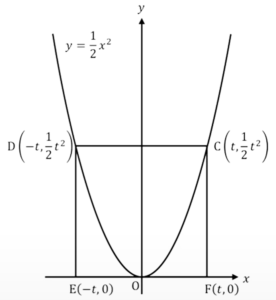
お決まりで、Cの\(x\)座標をTと置いてしまいます。Cの座標は\((t,\frac{1}{2}t^2)\)になります。そうすると四角形はCDEFの順に回るので、Dは\(y\)軸に対してCと対称な点なので、\(-t\frac{1}{2}t^2\)と置きます。

で、EFは\(x\)軸上にあるので\(y\)の座標は0と\(x\)軸の座標は、EはDと同じ、FはCと同じTということになり、このような図になります。

\(C(t,\frac{1}{2}t^2)\)とおく

このような条件で、CDEFが正方形になればいいわけですから、縦横の長さが等しければいいわけです。これを式で表してあげると、横の長さは2tになります。高さは、\(\frac{1}{2}t^2\)になるので、CDとCFが等しいという式はtを用いて書き表すと、こういうことになります。

\(CD=CF　2t=\frac{1}{2}t^2　　t^2-4t=0　　t(t-4)=0\)

で、これを用いて整理するとこのような形になるわけですが、tは正なので0にはなりません。0だと点になってしまいますので、それを完備するとtは4っていうことになります。

そうすると\(y=\frac{1}{2}x^2\)の点なので、\(x\)座標が4、\(y\)座標は\(\frac{1}{2}4^2\)ということで、Cの座標は(4,8)ということになります。

\(t >0 より　t=4　　C(4,\frac{1}{2},4^2)=(4,8)\)

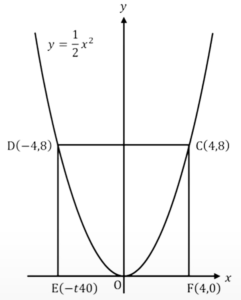
ちなみに、これは聞かれてないけど後で必要になることですが、Dの点は、CDは\(x\)軸に平行なので、CとDは\(y\)軸に対して対称、よってDは(-4,8)ということになります。

さて、後半を見ていきます。三角形AC、GBが平行四辺形になるときです。

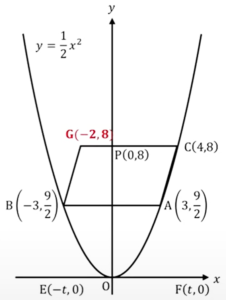
このような形になります。

AC=BG,　AC || BG

平行四辺形の問題は、直線の式を出してもいいのですが、平行四辺形なので長さも傾きも等しいので、下図の右三角の増分が、左三角の増分と等しいとして出した方が、圧倒的に早く求めることができます。

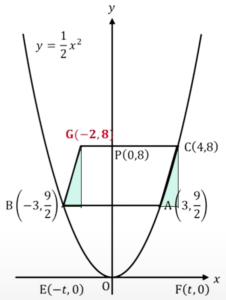
なので、ここの\(x\)の増分は4-3で1、\(y\)の増分は\(8-\frac{9}{2}\)です。だからBがGに行く時も同じだけ増えるわけですから、Bの元々のマイナス座標に4-3を足します。\(y\)座標は\(\frac{9}{2}\)に3、\(8-\frac{9}{2}\)を足すということで、ここの点は(-2,8)ということになります。

\(G(-3 + (4-3), \frac{9}{2}+(8-\frac{9}{2})=(-2,8)\)

A.　点C = (4,8)、点G =(-2,8) 

 

(4)　(3) のとき、線分CDと\(y\)軸との交点をP、直線BGと\(y\)軸の交点をQとする。△PGBの面積を\(S_1\)、△PGQの面積を\(S_2\)とするとき、\(S_1：S_2\)を求めなさい。（求め方や途中の計算をかくこと）

方針は、ここを\(S_1、S_2\)が青と赤のところになってますので、CDを底辺として見ると、底辺が共通なので、面積の比はこの三角形の高さの比になります。

つまり、\(S_1\)の高さと\(S_2\)の高さの比が分かれば、それがそのまま面積比ということになります。

なので、Qの座標の情報が欲しいのでそれを求めたいのですが、それは直線BGを通るので2点を通る直線です。2点を通る直線は次のように立式でき、計算することができます。

直線BGの式は
\(y-8=\frac{8-\frac{9}{2}}{(-2)-(-3)}(x-(-2))\)
\(y=\frac{7}{2}x + 15\)
\(Q(0,15)\)

そうすると、下図の①の高さは15-8で7、②の高さは8-\(\frac{9}{2}\)で\(\frac{7}{2}\)になりますから、S1とSPの比は\(\frac{7}{2}：7\)ということになります。

これを簡単な整数比に直してあげると答えは1：2、ということになります。

\(S_1：S_2\)は、GPを底辺（共通）とすると△PGBと△PGQの高さの比 PH：QP
\(S_1：S_2 = PH：QP = 8-\frac{9}{2}：15-8=\frac{7}{2}=1：2\)

A.　1：2 

 

(5) (3)のとき、AR+RGが最小になるような\(x\)軸上の点Rの座標は（　　,　　）である。

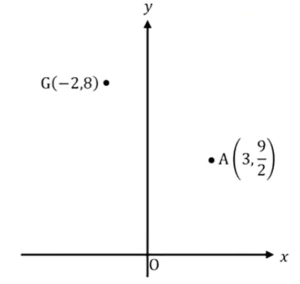
この問題の考え方ですが、aと\(x\)軸に対してaと対称のa’です。座標で表すと\((3,-\frac{9}{2})\)になりますが、このようなものを取ってあげます。

\(x\)軸に対してAと対称な点をA’とすると A’\((3,-\frac{9}{2})\)

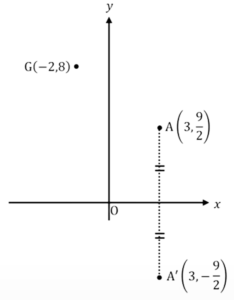
そうするとRは\(x\)軸上の、どこかにあるわけですね。

例えば下図の場所にRがあったとすると、Aから\(x\)軸までと、A’から\(x\)軸までが「長さ」になるわけです。

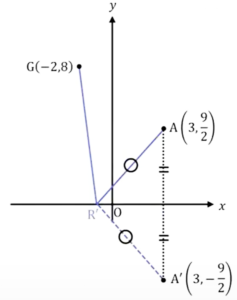
ただし、対称に持ってきて、\(x\)軸が中点を二等分している垂直線になっているので、二等辺三角形になっている、つまりAから\(x\)軸までと、A’から\(x\)軸までは長さが等しいわけです。

ということは、図に書いた〇と〇の部分、R’からAと、R’からA’の長さは等しい、ということです。

つまり、R’からA’の長さを最小にするところを求めればいい、ということになるので、それはGとA’を直線にした時、その時の交点が求めたいRになります。

\(x\)軸上の任意の点をR’とすると AR’ = A’R’
よって AR’ + R’G = A’R’ + R’G
これが最小になるのは、A’Gが直線のときなので、求めるRはA’Gと\(x\)軸の交点
求めるRはA’Gと\(x\)軸の交点

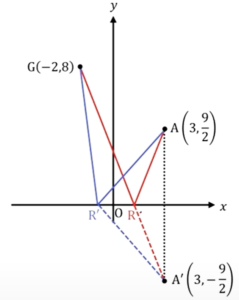
さて、この直線の式を求める必要がありますが、これも2点を通っている直線の式なので、以下のように立式できて、計算できます。

A’Gの直線の方程式は
\(y-8= \frac{-\frac{9}{2}-8}{3-(-2)}(x-(-2))=-\frac{5}{2}x-5\)

Rは\(x\)軸上にあるから、この時\(y\)座標が0です。そうすると、この式で\(y\)を0と置いて\(x\)を求めれば\(x\)は\(\frac{6}{5}\)となるので、この点で\((\frac{6}{5},0)\)ということになります。

\(y=-\frac{5}{2}x+3\)
\(y=0\)とおいて、\(0=-\frac{5}{2}x+3\)
\(x=\frac{6}{5}\)
\(R(\frac{6}{5},0)\)

補足：2点を通る直線の方程式

ちなみに、今回も2度ほど使ったのですが、2点を通る直線の方程式をちょっと補足しておきます。

直前の問題でも、

A’Gの直線の方程式は
\(y-8= \frac{-\frac{9}{2}-8}{3-(-2)}(x-(-2))\)

この箇所で使用しています。

例えば、\((x_1, y_1)\)という点と、\((x_2、y_2)\)という点があったとき。

この2点を通る直線を求めようとした時に、傾きは\(\frac{(x_2, y_2)}{(x_1, y_1)}\)なので、傾きは\(\frac{y_2-y_1}{x_2-x_1}\)になります。

これがどっちを通るとしても同じ答えは出てくるんですが、例えば\((x_1, y_1)\)の点を通るとすると、\((x-x_1)\)を付け加え、\(y-y_1 =\)と置くことによって立式されるわけですね。

\(y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)\)

それを直前の問題で使っています。

展開すると\(x\)の係数に\(\frac{y_2-y_1}{x_2-x_1}\)がかかってきますので、これは確かにこの直線の傾きであるということが分かるわけです。

そして、これに\(x_1\)と\(y_1\)を代入してあげると、左辺は0、右辺は0でこの等式は成り立ってるから、\(x_1\)と\(y_1\)はこの直線上にあるということも分かるわけです。

なので、よくあるのは連立方程式ですね。\(y=mx+n\)とおいて、2つ式を立てて連立方程式を解くという解き方を、特に学校なんかでは教えるのですが、時間もかかるしめんどくさいので、2点を通る直線の式は\(y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)\)を使ってサクっと立式できるようにしておく方が非常にいいかと思います。

今回の問題の中でも2回使ってますし、よく使う式です。

まとめ

以上、令和2年の一般入試数学「関数(1次,2次)と図形」について見てきました。過去関連記事はこちら↓
川崎医科大学附属高校の入試対策
→【2025年版】川崎医科大学附属高校 数学 過去問解説｜小問集合
→【2025年版】川崎医科大学附属高校 物理 過去問解説│力学

講師：江口和弘 ＜経歴＞ 東京農工大学工学部卒業 東京大学大学院工学系研究科修了 一般企業で研究職として活躍後に、塾講師へ転身しました。大学補習の物理系科目をメインに活躍しています。明るく親身な指導が特長で、これまで何人も単位取得に導いています。