こんにちは。究進塾編集部です。今日は新井先生の数学史「第3回-後編」をお届けします。前回の内容では、虚数が登場した背景を追いかけてきました。

今回は、発見してしまった虚数を、数学の天才たちはどう捉え、受け入れていったのかについて解説していきます。

２次方程式の次は3次方程式…

けれど、2次方程式に対して、次は3次⋯皆さんだんだん怖くなってきますよね。

2次方程式について、ちょっと歴史的なものを調べると、紀元前の3000年とか5000年にまで遡さかのぼるんですね。

古代エジプトとか、あとはメソポタミア文明とか。メソポタミアっていうのは今のイラクとかになるんですけど、「川と川の間」っていう意味らしいんですね。川と川の間の栄えた文明ができてきます。

エジプトの場合は、ナイル川の近くで必ず毎年決まった時期に氾濫が起こります。時期が決まっているので「それを何とかしよう」ということで図形の測量などにつながったっていう話があります。

キュウちゃんのマメ知識 ナイル川の基礎情報 ナイル川は全長6,690km、世界最長の川。日本列島は最北端の択捉島から最南端の沖ノ鳥島まで約3,000kmだから、倍以上あるキュ！ ヴィクトリア湖から流れる白ナイル、エチオピア高原から流れる青ナイル。この2つがスーダンのハルツーム付近で合流し、地中海に向かって流れていくキュ。 “エジプトはナイルのたまもの” 古代ギリシアのヘロドトスが『歴史』で述べた言葉キュ。意味は、ナイル川が氾濫を起こすと土壌が肥沃になるため、エジプトはナイル川のおかげで文明が栄えた、ということキュ。 ナイル川の氾濫 9月中旬〜10月上旬に、下流が自然堤防から溢れて、1ヶ月間そのまま留まるキュ。エジプトは雨がほとんど降らないけど、この氾濫があることで農業が可能だったんキュ！ 氾濫の理由は、上流のエチオピア高原が8〜9月に雨期を迎えるキュ。その水が集まって下流域のエジプトで氾濫が起こるんだキュ〜。 ナイル川が運ぶ栄養 ナイル川の氾濫は、水だけでなく栄養素も運んでくるキュ！カリウム、リンなど、有機質が豊富な土地に、毎年生まれ変わるんだキュ〜！

なので、2次方程式自体は、もう紀元前3,000年とか5,000年の人はやってたんですね。生活に必要だからやらざるを得ないっていう。

なんですけど、今だったらこのように文字で「\(x\)を求めなさい」みたいにやりますけど。

（例）
\(ax^2+bx+c=0\)
\(2x^2+3x+1=0\)
\(x=\)　…

こういうことはまだやっていなくて。

具体的に「1個1個の方程式を解く」というのは、60進法とかでやっていたことは残っているみたいなんですが、それをちゃんと体系的に「この場合はこう」「この場合はこう」みたいな「まとめて公式にする」っていうところまでは、やっぱりたどり着かないっていう段階でした。

公式をちゃんと発見できてたのは、ちょうど7世紀ぐらいに、インドでブラマグプタという人です。以前紹介したインドの人です。

\ 0の概念を書いた現存最古の書！ / ブラフマグプタ（Brahmagupta） [生没年：598-665以後] インドの天文学者、数学者。インドやイスラムの天文学に大きな影響を与え、不定方程式や図形の問題で数学者としての才能が発揮した。

この人は公式は発見できてはいるものの、言葉で説明している程度で、今みたいな…これ中学生でやるんですけど、覚えてますかね？

\(x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)

これ中学校3年生でやるんですね。で、あの2次方程式の解の公式を英語で調べると「midnight formula」っていうのが出てきます。「”真夜中の公式”ってどういう意味だ？」っていうツッコミを最初は入れてたんですけど。

「自分の体の中に染み渡るまで、暗唱できるまでちゃんと言えるようにしろ」みたいな、そういう意味が込められていて。「夜中に叩き起こされても言える！」みたいな、そういう公式としてこれが上がってくるんですね。

だから、これ歌になってたりするんですよね。海外のいろんな人が歌にしています。Youtubeにもあります。このことをいろんな人に紹介すると「なんでこんなに歌うまいの？」とか歌の方に注目してしまって、解の公式を全然扱ってくれないんですけど。(笑)

「\(\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)なんて長くて覚えられないよ！」っていう。

これ、中学校で1番長い公式なんです。

公式って、円の面積とか球の体積とかいろいろやりますけど、こんな長い公式は中学生では、多分やらないと思うんですね。なのでこれが一番、中学生で習うものでは長い公式として知られています。

2次方程式だけでこんな面倒くさいのに、今度は3次方程式を考えようとしてるんですね。もっと厄介です。

僕も3次方程式と4次方程式の解の公式は覚えられないです。あれは見ながらじゃないと分かりません。

それはどういったものかっていうのを、今は歴史的な流れとして話を進めているので、その視点で見ていきます。

3次方程式とはどういうものか

3次方程式の話をしていたんですが、3次方程式の中で、こういう問題を取り上げていたんですね。

\(x^3-15x-4=0\)

1番大きいところが「3（\(x^3\)のところ=指数）」になってるので、これ3次方程式って言うんですけれど。

当時、16世紀のイタリアなんですけど、この時は今みたいに学術論文とか学術紀要みたいなものがありません。自分がやったことを「〇〇アカデミー」「科学アカデミー」みたいなところで残せるっていうところまで進んでないので、自分が残した公式とかそういうのをどうやって世に残すか、みたいなものが今とは全然違うんです。

どういうもので残すかって言うと、数学の試合で、自分たちの発見した公式を試すんですね。

「数学の試合」って言われても想像するのが難しいと思いますが…今で言うと「数学オリンピック」みたいなそういうイメージがいいかなと思います。お互いに何個か問題を出し合って、多く解けた方が賞金を得られるとか、名誉を勝ち取るとか。

そういうところで3次方程式という解の公式を知ってることによって「相手が知らない問題でこっちが解けるから強いよね！」っていうことで、カルダノさんは2次方程式の解の公式以降の、3次方程式の解の公式を知りたかったんですね。

知りたかったので、当時知られている別の人で、3次方程式の解の公式をもう発見している人がいたんですが、その人にコンタクトを取って「ちょっと方程式の、この公式、教えてもらえない？」って聞きに行くんですね。この人は頭がいいので。

で、その公式を使って当てはめると、ものすごく複雑になっている方程式なので、もちろん解の答えもそんなに簡単な形ではなくって、解いてみるとこんな感じになります。

\(x=\sqrt[3]{2+\sqrt{-121}}+\sqrt[3]{2-\sqrt{-121}}\)

「√の中にまた√に入ってんの？しかもこの√の前にくっついてる3って何だよ」っていう話なんですけど。

これは2乗したら2になるものを「平方根」って言うんですけど、この3っていうのは、例えばもうちょっと簡単なやつで言うと、「3乗したら2になるもの」を次のように書くんですね。

\(\sqrt[3]{2}\)

これを、3乗根と言います。

これは高校2年生で、文系でも学習する「指数」っていうものです。指数関数の単元で習うんですけど、大きい数とかちっちゃい数とかを扱う時に、これを習います。

大きい数、小さい数の例 大きい数で言うと、例えば「折り紙を何回折ったら月にたどり着く」っていう問題とか。あとはドラえもんの道具で言うと、栗饅頭か何かに薬をかけると2倍に増えていくっていう、そういう薬があって、それで最後は栗饅頭が増えすぎて宇宙を追いつくしてしまうって「やりすぎた！」っていうオチの話があるんですけど。大きい数はそういうものがありますね。 逆に、ものすごくちっちゃい数だと、細菌の菌の増殖の度合なんかを計算する時があげられます。コロナでもよく言いますよね。「指数関数的増加」とか。そういうところで数学の用語が使われます。こういう時に、数学をやってるとそれがよく分かるんです。

つまり、これは3乗したら2になる根っこ・元のことを言います。

だから中学校でやっている√2っていうのは、実は2が隠れているんです。

\(\sqrt[2]{2}\)

「2乗したら2になる」っていうふうに考える。他にも\(\sqrt[5]{3}\)（5乗したら3になる）とかね。こうやって、一応「なんでもありか！」みたいな。そういう感じになります。

だから、さっきの\(\sqrt[3]{2+\sqrt{-121}}\)は「3乗したら \(2+\sqrt{-121}\) になる」っていうことなんです。「なんでこんなのが出てくるんだ？」っていう話なんですけど、これはさっき\(\sqrt{-1}\)っていうのをデカルトさんは「\(i\)」というふうに書くっていうね。

\(\sqrt{-1}=i\)

だからこれは今で言うと、

\(\sqrt{121}i\)

って書くんですけど、\(\sqrt{121}\)って、11の2乗なんですね。11を2回かけると121なんですね。だからこれ元々、11なんです。

もうちょっと簡単に書くといいんですけど。\(i\)っていう記号を使って書いてあげるとこんなふうになります。

\(\sqrt[3]{2+11i}+\sqrt[3]{2-11i}\)

ちょっとだけすっきりしました。ちょっと折りたたんだような感じですね。

3乗したら2+11iになる根っこは何？っていうところでこんなのが出てきちゃうんですけれども、「こんなの意味わかんないよ」っていう話ですが。

ボンベリの発見

こういうところで、もう1人数学者が出てきます。

今はカルダノさんをご紹介しましたが、今度はボンベリっていう人が出てきます。

\ 虚数が気になって気になって / ボンベリ（Rafael Bombelli） ［1526年 – 1572年］ イタリア・ボローニャ出身の数学者。代数学、特に虚数の理解と応用に大きく貢献。それまで謎とされていた虚数の研究を積極的に行った。

この人はそんなに有名じゃないのかな、という人ですが、この人が\(\sqrt[3]{2+11i}\)をもうちょっと計算しようとして、違う変形式からこれに近いものを出したんです。

\(2+11i\)が\({(2+i)}^3\)というのを、別枠で計算してるんですね。そして\(2-11i\)を\({(2-i)}^3\)で計算しています。それらの結果は\(2+11i\)と\(2-11i\)になりますよ、っていうのをやってるんです。

「3乗したら\(2+11i\)になる元は\(2+i\)なんだよ」っていうのを発見しちゃってるんです、どこかで。「その背景どうなってるんだよ」って話なんですけど。

でも、\(\sqrt[3]{2+11i}\)ってめちゃくちゃ難しいんですけど、\(2+i\)になるんです。\(\sqrt[3]{2-11i}\)も\(2-i\)になります。

\(x=\sqrt[3]{2+\sqrt{-121}}+\sqrt[3]{2-\sqrt{-121}}\)
\(=2+i + 2-i\)

「こんなに難しいのに、\(2+i\)、\(2-i\)なのか！」みたいな。さらに、計算した結果「\(i\)」が消えちゃうんですね。答えは「4」になるっていう。「なんだこの魔法は」みたいな。数学者、やたらと「魔法使い」っていうふうに言われるんですけど。

これは、今はこんな面倒くさい計算はしないです。高校生、こんなことやってたら大変です。もうみんな数学嫌いになります。ただでさえ嫌いなのに。

で、これ4になるってことは、こんなめんどくさい、「この箇所“\(\sqrt[3]{2+\sqrt{-121}}\)”に何かしら意味が隠されてるんじゃないか…？」っていう発想をするんですよね。「おそらく不思議な何かがここにはたらいてる！」っていう発想をします。「じゃなかったらこんなシンプルな答え出るわけない！」っていう。

っていうのが今度は、数学者たちの関心を惹きつけていくんですね。こんなに複雑に絡まったロープなのに、あるきっかけでスルっと全部ほどけるみたいなそういうものを、こいつがメッセージとしてみんなに与えてしまう。

これにはどういう意味が？と考える数学者たち

これ実は、今で言うと「\(x\)の解の候補」と言って、\(x^3-15x-4=0\)の\(x^3\)の係数（=数のこと）が1の時は、「定数項」と言って約数「-4」がこの方程式の解の候補だ、ということを今は高校2年生で教えるんですね。

これ、-4の約数って何がありますか？いっぱいありますけど。

そうですね。あとはマイナスもOKです。-4、-1、-2もOKです。そのうちの4を入れたら成り立っちゃうんですね。

「さっきの作業の大変さは何だったんだよ！」みたいな話ですよね。逆に現代人が当時にタイムスリップしてこの人たちに数学を教えたらどうなるのか、っていうのも見てみたいところではありますが。

で、だから実は他に、3次方程式の場合は、解は3つです。基本的には。2次方程式の2個なので、字数がそのまま解の個数を表すことになるんですね。

「ということは、3次方程式にはこの√の中にわけわからないのが入ってきてても、何かしら意味があるものが出てきているんじゃないか？じゃあもうちょっと見方を変えていかないと…式変形を色々していくというアプローチだけだと、ちょっとなかなか進まないよね…。というか、理解進まないよね」っていうふうな見方をするのは、やはりどの時代でも一緒なのかな、という気がしてきます。

このシリーズの最初にやった「マイナスを掛け算する」っていう、発想を変えて原点に関して180度回転させるっていう発想。あれなんて本当に新しいというか、19世紀～20世紀の数学の考え方です。

結局、i（イマジナリーナンバー）とは？

一番最初に「\(-1×-1\)が1である」を回転で考えるっていう話をしました。それを、回転を止めたらどうなるかっていう話をすることによって、もう少し「\(i\)（イマジナリーナンバー）」を身近に感じられるように、距離をちょっと近づけられるようなお話ができたらと思います。

さっき、3次方程式の解の公式っていうのを使ってやってみた通り、3次方程式の解の公式というのが超複雑な形であるので、多分見た瞬間にみんなもう見るのをやめるかもしれないんですが、一応載せておきます。

3次方程式の解の公式（シンプルバージョン） \(ax^3+bx^2+cx+d=0\)の解は、\(a≠0\)のもとで、以下の3つ： \(x=-\frac{b}{3a}-\sqrt[3]{A}-\sqrt[3]{B}\) \(x=-\frac{b}{3a}-ω\sqrt[3]{A}-ω^2\sqrt[3]{B}\) \(x=-\frac{b}{3a}-ω^2\sqrt[3]{A}-ω\sqrt[3]{B}\) ただし、 \(p=\frac{-b^2+3ac}{3a^2}, q=\frac{2b^3-9abc+27a^2d}{27a^3}\) \(A=\frac{3\sqrt{3}q + \sqrt{27q^2+4p^3}}{6\sqrt{3}}\) \(B=\frac{3\sqrt{3}q-\sqrt{27q^2+4p^3}}{6\sqrt{3}}\) \(ω=\frac{-1+\sqrt{3}i}{2}\)

ここで、19世紀に戻ります。ボンベリさんたちの時代からはまた400年ぐらい最新に戻ります。

\ 数学は科学の女王であり，整数論は数学の女王である / ガウス（Karl Friedrich Gauss） ［1777～1855］ ドイツの数学者・天文学者。著書『整数論』ほか。アルキメデスやニュートンと並んで「世界三大数学者」といわれる。多方面に活躍し、純粋数学、電磁気学に多くの業績を残し、近代数学のほとんどの分野に影響を与えた。

この人の名前は、磁石の単位になってます。「ピップエレキバン」っていう、磁気の力で肩こりをほぐす商品があるんですけど、あれに「ガウス」と書かれていますが、それはこの人ですね。

この人、生まれた年が覚えやすいんですよ。ゾロ目なんです。1777年っていう、トリプル7になってるので覚えやすい。なくなった年も1855年で55がゾロ目で、年だけは覚えられちゃいます。

けれど、ちょうどこの人の時代に、前お話ししていた数直線に対して原点があって、\(1\)があって\(-1\)があって…\(×(-1)\)の話をこんなふうにした時に180°回転させましたよね。

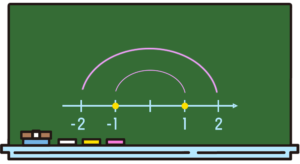
で、この人の時代はもっと先進んで「回転を途中で止める」っていう。どういうことかって言うと、180°じゃなくて90°で回転を止めちゃおうと。

ということは軸が空間の上のどこかにいるから、横軸じゃ足りないよねってことで、また新しいことをやり始めます。ここで縦軸を加えちゃうんですよね。

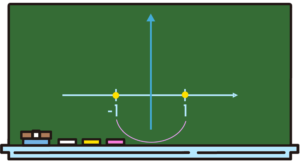
今までの横ラインにいる数たちっていうのは、自然数と整数と有利数・無理数ということで、全員実数なんです。なので、実数の人たちがいるということで”real”の「Re」って書くんですね。

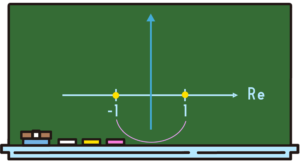
で、ここにいる人たちっていうのを、さっきやった「\(i\)（イマジナリー）」たちを縦軸に置いて成立させるっていうことで「Im」と書きます。

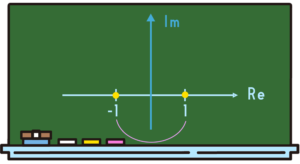
そうすると、180°の途中、90°で回転を止めるので、その到着した場所を「\(i\)」というふうに定めようっていう話になってきます。

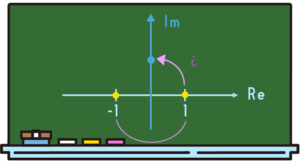
「\(× (-1)\)」したときには180°回転しますよね。この発想で言うと、今度「\(× i\)」をすると90°の回転とみていいんじゃないですか？と、同じ発想をするんですね。

・「\(1\)」に「\(×(-1)\)」をすると180°回転
・「\(1\)」に「\(× i\)」をすると90°回転

じゃあ、もう1回「\(i\)」をかけて「\(1 × i × i\)」をすると、どこに行きますか？

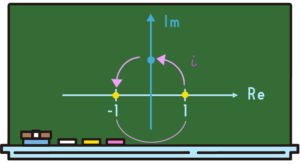
ここに行きますよね。だから「\(i\)の2乗」って、結局は「\(-1\)」になるんですよね。

これを実は数学Ⅱで、いきなり「こう定義する」って習います。無理ですよね。だって、教科書にこの図ないんですから。これやるの数Ⅲなので。

これをどうやって解釈すればいいかって言うと「90°を2回転」なんですよね。だから\(i\)を3乗したらもう1回行くので、ここに行きます。

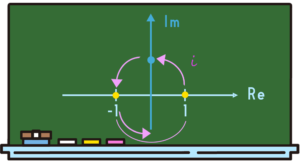
これは「\(-i\)」です。そして、もう1回かけたら元に戻りますよね。\(i\)を4回かける、つまり「\(i^4=1\)」になります。

数Ⅱの教科書にある問題って、「\(i^4=1\)」みたいな、こういうのばっかりやってるんです。だから全然面白くないんですよね。それが何を表してるかが分かんないんです。だから本当に計算が好きな数学者みたいな人だったら、クイズ形式で「計算こういうふうになるよ」ってなるような、そういう人はいいんですけど、基本的にみんな意味を知りたがるので、こういうふうに意味を与えて。

平面にして考えて、実数に対して虚数を加えた世界、これをガウスは「複素数」と呼びました。「複数の要素でできてる数」、つまり横方向と縦＝上下方向でできてるのでこのように言います。

「複素数」を英語で「Complex Numbers（コンプレックス ナンバー）」と言います。記号はCに二重線を入れてあげて「ℂ」となり、この複素数っていう世界を追加して、数の世界はこうなります。

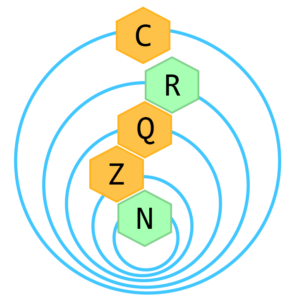
こんな感じです。一番外側のℂの世界に「\(i\)」っていうやつがいます。\(i\)は「\(\sqrt{-1}\)」のことです。\(\sqrt{-1}\) がいます。

それぞれの世界には、こんなのがいましたね。

「ℝ」の世界：「\(\sqrt{2}\)」とか
「ℚ」の世界：「\(\frac{2}{3}\)」とか
「ℤ」の世界：「-1」「0」とか
「ℕ」の世界：「1」「2」「3」とか

ということは、足し算、引き算、掛け算、割り算とか、やっぱりしたいよねってなる。

「またかよ」みたいなね。それで、最初のところに戻ります。「新しい数を作ったんだから、足し算・引き算・掛け算・割り算やりたいじゃん」っていうふうになるので、それだったら、実数と合体してるからℂの数としては「\(2+3i\)」とかこういうのもいいじゃん、っていうことになります。

これは実数と虚数が合体してるので、\(2+3i\)っていうのもいいし、「\(2-3i\)」とか「\(2+\frac{3}{2}i\)」とかなんでもいいんですよね。

こういうのをひとまとめにして、こうやって書いちゃいます。

\(a+bi\)

そうすると、「\(a\)」が実数で\(i\)にくっついてるものが虚数の部分なので、これ名前があるんですね。そのままなんですが、実数の部分なので「実部」って言います。こんな形してるんです。

□＋△\(i\)

□の部分を「実部」、△の部分は虚数にくっついてるから「虚部」って言います。

なので実部っていうのはさっき言った「real」の部分なので、「Real part」っていいます。これもそのままです。で、虚部の方は「Imaginary part」って呼んじゃいます。

というふうにすると、さっきの「Re」と「Im」というのは、ここの頭文字を取ってますね。

それで、複素数というのが数の世界を広げましたっていうところまで到達します。

でも「数を作ったはいいんだけど、結局それってどこにいるの？」っていうのが分からないとなんかこう気持ち悪いな…っていうのは残ると思うので、ガウスさんはこれに対して、せっかく軸をもう1個加えて縦軸を作ったんだから、その軸っていうものを元にして、平面と考えてこれを「複素数平面」って言います。

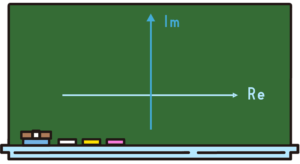
「Complex plane」っていう。

で、さっきこの「\(a+bi\)」っていう数で、例えば「\(3+2i\)」ってどこにいるの？っていうのを表現したかったら、3は横軸方向、2は上下方向なので、「\(3＋2i\)」はここにいますっていう意味です。

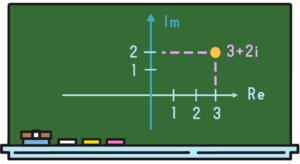
もし、「\(3+2i\)」の3がなかったとしたら、そのまま「Im」の軸上の2のところに「\(2i\)」というのがいます。

どこに住んでいるかがわかるんですね。数を変更しても大丈夫です。「\(\sqrt{2i}\)」だとしたら、\(\sqrt{2}\)は大体1.4ぐらいなので、「Im」軸上の1と2の間あたりにいますね。

だから平面上に、実数が横軸のところにいて、他の「〇〇＋〇〇」とかは線以外の空白のどこかにいるよ、というふうにすると「それはどこにいるんですか？」と聞かれたときに「ここにいますよ」みたいに言ってあげられるようになります。

まとめ

ということで、今回は方程式のちょっとした歴史と、今までやってきた数の世界を、自然数から複素数の世界まで広げてお話をしてきました。

数Ⅱの内容を言ったり、数Ⅲの内容をちょっと言ったり。色々な時代を行き来してるので、教科書の順番ではお話してないです。っていうか、そうならないんですよ。ちゃんと流れを追って見ていくと。

なので、もし自分で勉強していく時に、必ずしも数Ⅰ→数Ⅱ→数Ⅲという順番でやらなくても、楽しむことはできるよっていうのを知ってもらえればいいのかなと思います。

次回は、今回せっかく3次方程式のお話をして、カルダノさんとかのお話をしたので、方程式の歴史をちょっと次回はお話ししたり、無理数の歴史も。円周率とかね。

円周率はやりだすと大変です。アルキメデスさんとか、日本の数学「和算」の話を絡めて無理数の話を辿りながらやっていきたいと思います。

和算とは 日本人の数学者については、教科書ではあんまり取り上げられないかもしれないですが、日本史の教科書で扱っているとしたら関孝和という人とか、あとは『塵劫記』って言って江戸時代当時のベストセラーになっている数学の本があるのでそれぐらいは資料集とかでよく出てきます。そこら辺の江戸時代の数学のことを「和算」といいます。

ということで、今日は3回目の内容で数の世界を結構広いところまでやりました。これを期にいろんな数の世界を楽しんでいってください。

＜第4回へ続く！＞

動画バージョンはこちら→