こんにちは。究進塾 編集部です。

江口先生の電磁気学の解説シリーズ、第4回です。電気力線とGaussの法則の解説です。

電気力線（でんきりきせん）

電気力線とは

まず電気力線なのですが、電気力線とは何か具体的に言うと「電場の様子を可視化したもの」です。だから実在するものではないんですが、電場の様子を表すために曲線を引いて考えます。そうやって引いたものを「電気力線」と言います。

例えば、

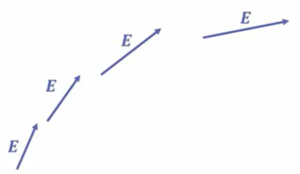
図のように、各点の電場がこのようにあったとすると、この電場のベクトルが接線になるような曲線を引きます。

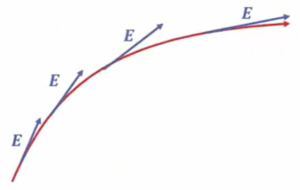
赤い線のように引きます。このように引いた曲線のことを「電気力線」というふうに呼んでいます。

イメージとしては、よく天気予報で「風の向き」と「強さ」（天気予報の場合は大きさではなく緯度で示されることが多いです）が天気図の上に書かれていると思います。それを繋いでクネクネとした線が引かれていると思うんですが、天気図で言うと風の向きに相当する矢印で書かれているのが「電場」に相当します。それで線がつながっていってます。

これは流体力学で「流線（りゅうせん）」と言いますが、電磁気学では「電気力線」と呼んでいます。このような線を総称して「電気力線」と呼んでいるわけです。

電気力線の性質

電気力線の性質なんですが、まずはプラス電荷から出ます。

プラス電荷から出た電気力線は、図のようにマイナスの電荷に入っていく。このような線になります。

あるいはマイナスに入らない場合は無限遠までいってしまうということになります。

なのでプラス電荷から出る電気力線っていうのは、マイナス電荷に入るか無限大に行くかということで、このような線になるわけです。

 

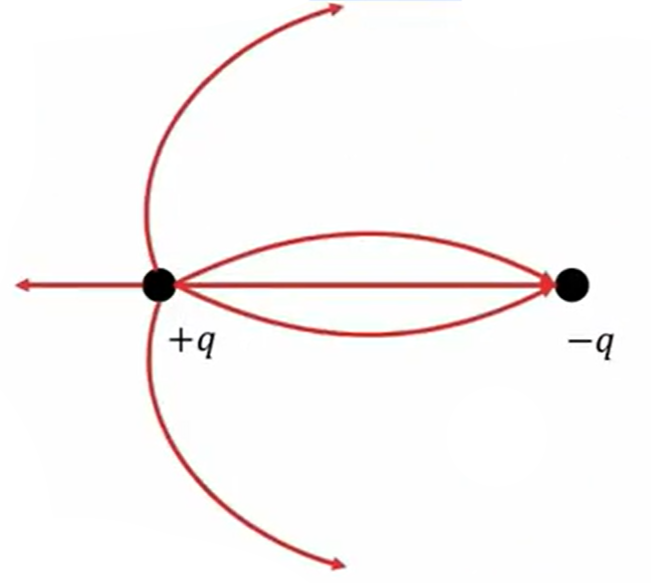
逆にマイナスの電荷に入る電気力線は、プラス電荷から出てきたものか、あるいは無限遠から来たものがマイナスの電荷に入っていくということになります。

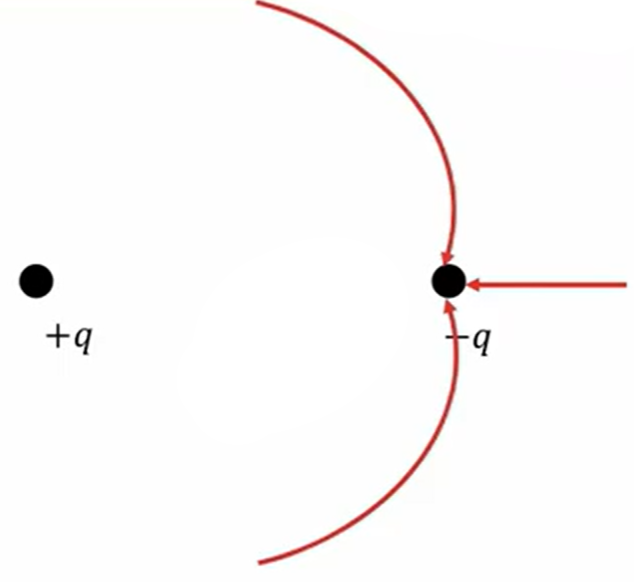
なのでマイナスの電荷に入る電気力線をまとめると、プラス電荷から出たものか無限遠から来たもの、こういうことになります。

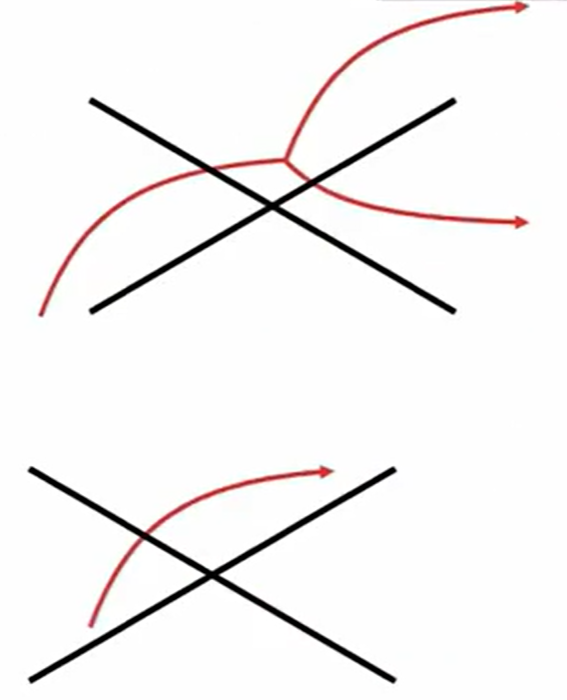
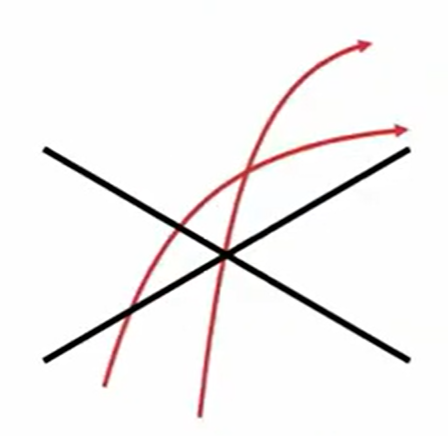
それから電気力線の性質なんですが、下図のように、途中で分岐（枝分かれ）したり、あるいは途中でプツンと止まってしまうということはありません。それからもう1つ、電気力線同士がこのように交差するということもありません。

このような性質を電気力線は持っています。

まとめ：電気力線 🔵電気力線とは ■電場の様子を可視化したもの ◆電場の任意の点の接線の方向が 電場 Eの方向になるように引いた向きをもった曲線 流体力学では「流線」と呼ぶ。 ◆ ＋電荷から出る電気力線は、－電荷に入るか、無限遠点にいく ◆ －電荷に入る電気力線は、＋電荷から出たものか、無限遠から出たもの ＋電荷から出る電気力線 －電荷に入る電気力線 ◆分岐したり、途切れたりしない ◆交わらない

電気力線の密度

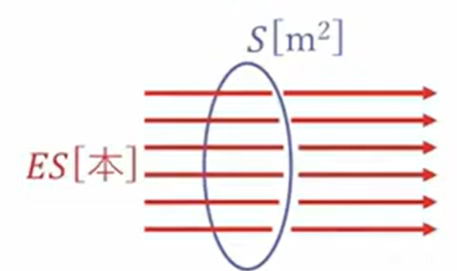
次に、電気力線の線の感覚です。密度はどのように考えるのかというと、定義としてここにありますように1平方メートルを通る電気線の数は、その点の電場の大きさEになるような密度で引きます。つまり「単位垂直断面積に、E本の電気力線が通っている」と、このように定義します。

そうすると当たり前なんですが、垂直断面積Sがあった場合には、ここにはES本の電気力線が通るということになります。

では、電気力線の方向と、通る断面が垂直じゃない場合ですね。その場合は、下図のように、傾けると実際に通るのは\(S\)の\(S \ cos \ θ\)という面積を電気力線が通るわけですから、この場合は通る電気力線の数は\(ES \ cos \ θ\)ということになります。

🔵電気力線の密度 ■単位垂直断面積にE本 ⇒垂直断面積SにES本 ■Eと断面が垂直でないとき \(ES \ cos \ θ = E・S\)

以前、面のベクトルについて「面に垂直な法線方向のベクトルで定義しますよ」というようなことをお話しました。この図でSと書いているベクトルですが、こういうベクトルで表されると、このことは「EとSの内積」という形に示されます。これが電気力線の数、密度ということになります。

電気力線の例

では、具体的に「電気力線がどんな形をしてるのか」を少し見ていきます。

電荷が1個の場合

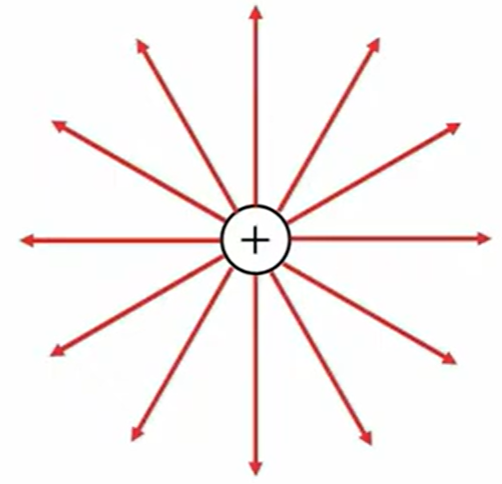
孤立電荷の場合、プラスの孤立電荷が1個あった場合は、これは等方的に直線的にこのように出ていきます。（等方的：物理量や物理的性質が、方向によって変わらないさま。）

逆に、マイナス電荷が単独であった場合は、無限遠からマイナスに向かって等方的に入ってきます。

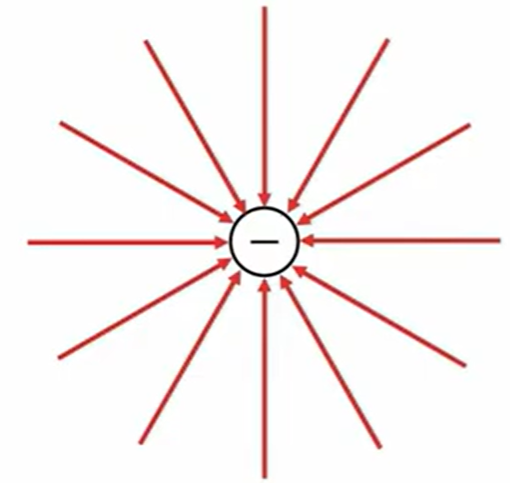
なので、孤立電荷の場合の電気力線の様子は、だいたいこのような放射状をした形になります。

電荷が2個の場合

次に、2個の電荷がある場合です。

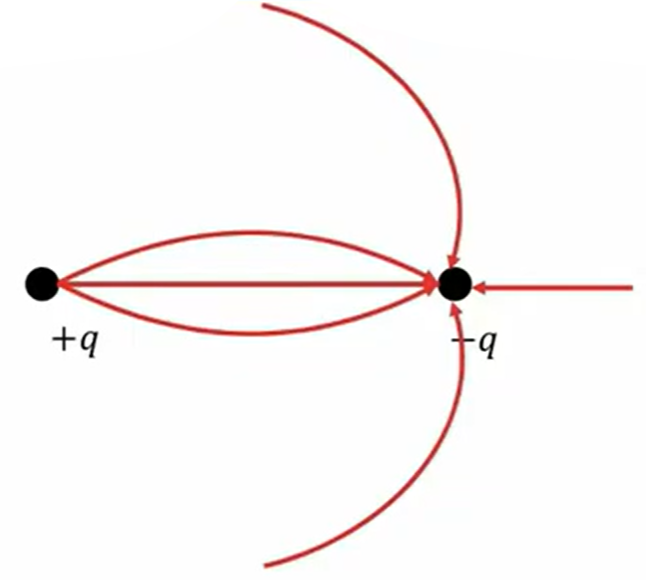
プラスとマイナス、つまり異符号がある場合、プラスから入ったものがマイナスに入るか、あるいは無限遠に行きます。マイナスに入る電気力線はプラスから来たものか、あるいは無限遠からやってくるということになりますので、これを徹底的に書いてみるとこのような形になります。

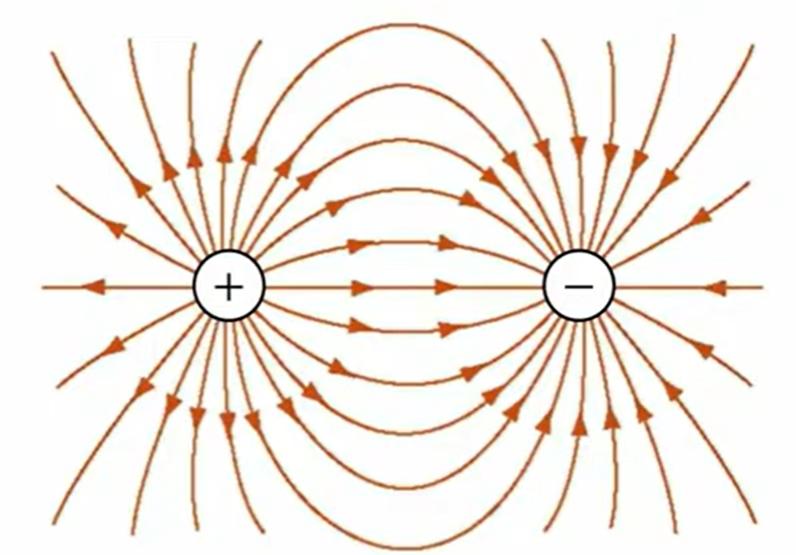
同符号の場合、ここではプラスとプラスを考えてみます。電気力線のプラスから出るものしかなくて、マイナスはないので、これは全部無限遠に行かなければならないわけです。なのでこのような形になります。

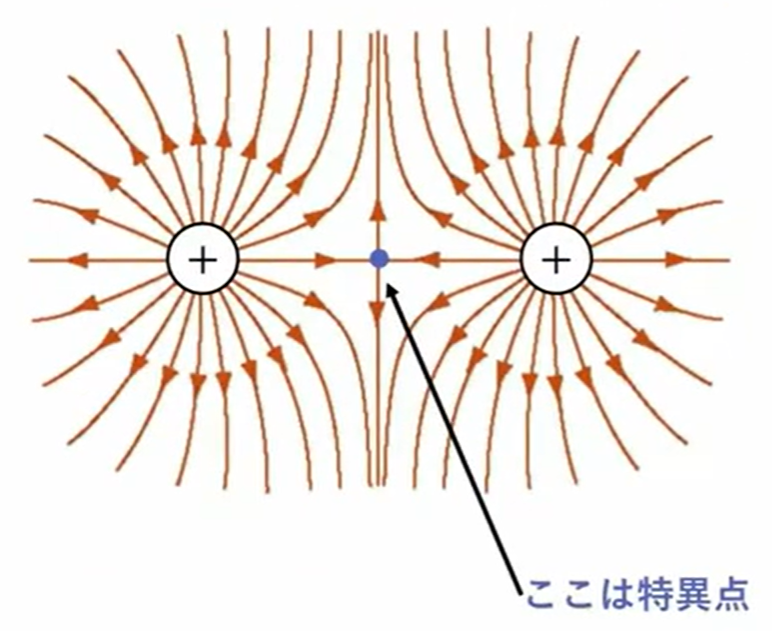
ただし、図の中心に書いた青の点、ここは電気力線がちょうどぶつかってしまって、あたかもここで止まったり枝分かれしたように見えます。

なので、電気力学では「この点を除外して考える」というふうに考え、ここは「特異点」ということになります。

無限に広い平面上正電荷

また次の例ですが、板状に均一に電荷が分布している場合です。

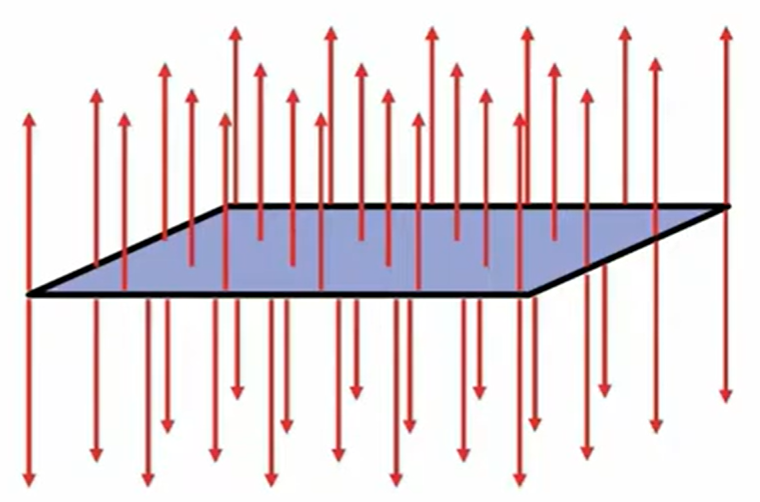
この場合はプラスの電荷が「一様に電荷している」ということを考えていますが、そうすると表裏に垂直に出ていきますので、この赤で書いてある垂直な平行な直線、これが電気力線の様子になります。

等電位線

さて、電気力線について4つの例を示しました。電気力線の様子は赤い矢印で書いていますが、これに垂直に交わる数の青い破線で示した箇所、これは「等電位面」です。電位が同じ点を結んでいくとこのような線になります。

ということで電気力線と等電位面は「直交」します。等電位面ということは「電位が0」ということを示していますので、直交するということが示され、横方向に見ると電位の変化はゼロということです。

なので等電位面というのは、直交することになって、孤立電荷はそれぞれ上の図のようになります。左から形を見ていくと、

・プラスの孤立電荷：球状
・プラスマイナスの2つの電荷：円が2つ
・プラスプラスの2つの電荷：電荷に近い電位は円に近いが、だんだんくっついてひょうたん型になり楕円型になる。はるか遠くに行ってしまうと球状になる。
・板状の電荷分布：青い破線で示した四角形の面が、すべて等電位面

Gaussの法則

電気力線の説明が終わったので、次にGaussの法則について説明します。

「Gaussの法則」というのは、教科書によっては「Gaussの定理」と書かれていることもありますが、以前の解説でも述べたように、数学に「Gaussの発散定理」と電磁気学の「Gaussの法則/Gaussの定理」というのは、非常に似ている形をしているのですが似て非なるものです。 そのため、ここでは区別しやすくするために「Gaussの法則」という名称を使って説明していきます。

これはどんなものなのかというと、

🔵\(Q[C]\)電荷からは\(\frac{Q}{ε_0}\) [本]の電気力線が出る

というのがまず1つです。

電荷が1つの場合

そうすると、ここに単位面積\(dS\)という面を考えると、

\(dS\)とEの内積が、ここから出ていく「電気力線の数」になるわけですから、こういう黒い点線で書いた閉曲面を書くと、電気力線は「閉曲面のどこからかは必ず出ていく」ということになるので、この微小面積\(E・dS\)を、　この表面積全体でぐるーっと全部積分してやったら総電気力線数、つまりこの内部にある電荷\(Q\)から出る電気力線の数\(\frac{Q}{ε_0}\)ということになります。それを式で表すと次のようになります。

\(\displaystyle \int_S E・dS = \frac{Q}{ε_0}\)

\(E・dS\)のこの平局面の面積分で表したものが、その中にある電荷、この場合は電荷\(Q\)がある場合だけですが、「\(\frac{Q}{ε_0}\)本が出ていきますよ」というのを、こういう形に表したもの、これを「Gaussの法則」と言ってます。

複数の電荷がある場合

では、複数の電荷が閉曲面内にあった場合です。

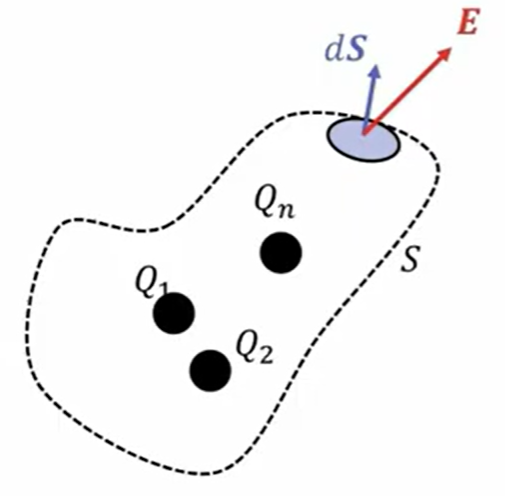
この場合、\(Q_1、　Q_2 …、Q_n\)まであるわけですが、以前学習したように電場は重ね合わせで表せますので、それでそれぞれの電荷 \(Q_1、Q_2、…、Q_n\)から出た電気力線のソースと考えることができます。

そうすると、先ほどの\(Q\)のところを、この閉曲面内にある電荷の総数（\(Q_1\)から\(Q_n\)までを足したもの）と置き換えると、ここに書いたように\(Σ\)（総和の記号）を使ってこのような形に表せます。

いずれにせよ、言ってるのは「右辺の\(\frac{〇}{ε_0}\)の分子に相当する部分は、考えている閉曲面の中にある電荷の総数である」ということが、重要なポイントです。

同じように考えると、点電荷じゃなくて連続した電荷分布を持った電荷があると。体積密度\(ρ\)で、連続した電荷密度を持ったものがあるとします。

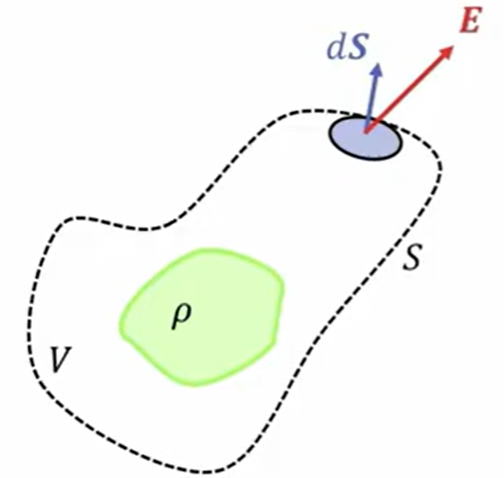
この閉曲面\(S\)の中にある単位面積\(ρ\)の電荷は、これを体積積分にしたものになるわけですから、総電荷量は次のように表せます。

\(\displaystyle \int_s E・dS = \frac{ \displaystyle \int_v ρdv}{ε_0} = \displaystyle \int_v \frac{ρdv}{ε_0}\)

Gaussの定理で厄介なところはここです。

Gaussの定理というのは、数学の定理でした。これは体積積分と面積積分の関係を表しています。

・Gaussの定理
\(\displaystyle \int_v ∇A dv = \displaystyle \int_S A・dS\)

このGaussの定理を、Gaussの法則に適用してあげると、面積積分を体積積分に変えることができます。そうすると積分の外側が全部揃ってしまいましたので、中側が等しいということで、微分演算子です。

\(∇・E = \frac{ρ}{ε_0}\) Gaussの法則の微分型

先に紹介した\(\displaystyle \int_s E・dS = \frac{ \displaystyle \int_v ρdv}{ε_0} = \displaystyle \int_v \frac{ρdv}{ε_0}\)が積分で表したものです。これはGaussの法則と全く同値で同じことを意味しています。

物理的にイメージしやすいのは、実は積分型の方がイメージとして捉えやすい、理解はしやすいです。数学的に式として解いていく場合は微分型の方がいいです。

なので、この2つを使っていくということになります。

Gaussの法則と電束密度

そして、Gaussの法則 \(\displaystyle \int_S E・dS = \displaystyle \int_V \frac{ρdv}{ε_0}\)、これの両辺に真空の誘電率\(ε_0\)というものを掛けると、下記の式のように変化する、と考えることができます。

\(\displaystyle \int_S ε_0 E・dS = \displaystyle \int_V ρdv\)

ここでベクトル\(D\)を\(ε_0E\)というふうに定義します。これを「電束密度」と呼んでいます。

電束密度：\(D = ε_0 E\)

Gaussの定理はこの電束密度を使うと、次のような形に書くことができます。

\(\displaystyle \int_S D・dS = \displaystyle \int_V ρdv\)

これの意味するところは、右辺は電荷の総量に相当しますので、\(Q\)の電束が電荷から出るという考えなわけです。

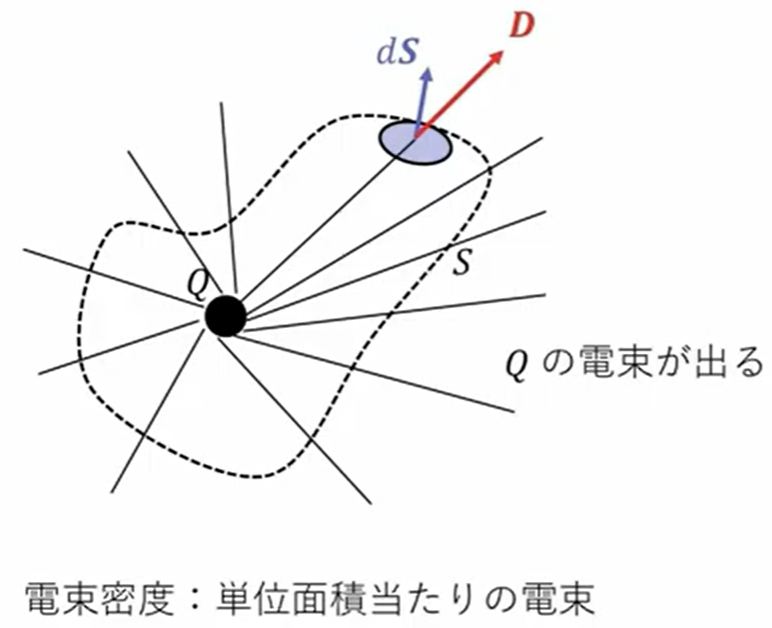
その時に、単位面積1㎡あたりを通る力線の数がD本である、このように考えることもできます。

これが電束密度で表したGaussの法則ということでございます。大事なことは「電束密度と電場にはこのような関係がありますよ」ということです。

Gaussの法則 ― まとめ ①積分型で表した場合 \(\displaystyle \int_S E・dS = \displaystyle \int_V \frac{ρ}{ε_0}dv\) 電束密度を使って表すと、 \((\displaystyle \int_S D・dS = \displaystyle \int_V ρdv )\)   ②微分型で表した場合 \(∇E = \frac{ρ}{ε_0}\) 電束密度を使って表すと、 \((∇D = ρ)\)

電気力線の方程式

では、話を電気力線に戻します。

電気力線の方程式、微分方程式がどうなるのかというと、これは定義通りでして、電気力線は電場が接線となるように引いたのが電気力線です。

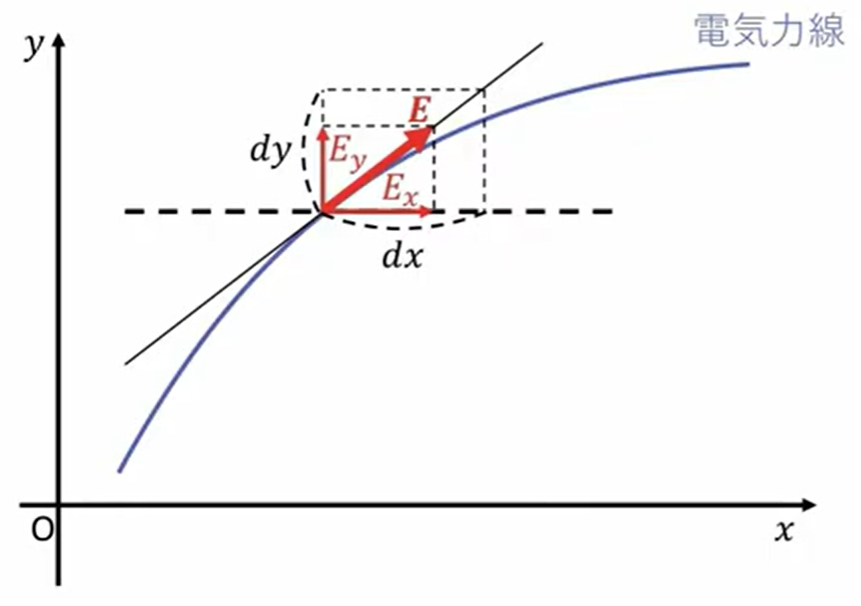
この図のように\(xy\)座標で表してやると電場\(E\)の成分が\(ExEy\)です。

で、この電場の方向に引いた接線（電気力線）、この時の傾きが\(\frac{dy}{dx}\)になるわけですから当たり前なんですが、このような式が成り立ちます。

\(\frac{Ey}{Ex}=\frac{dy}{dx}\)

これをちょっと書き換えてやると、このような形に表せます。

\(\frac{dx}{Ex}=\frac{dy}{Ey}\)

これちょっと書きやすいため二次元\(xy\)平面で考えましたけど、\(yx\)平面で考えても\(zx\)平面で考えても全く同じことが起こりますので、全部空間的に考えると次のような形になります。

\(\frac{dx}{Ex}=\frac{dy}{Ey}=\frac{dz}{Ez}\)

これが電気力線を表す微分方程式ということになります。

これを解けば、電気力線の曲線が関数形として出せるのですが、具体的には積分ができるケースがとても少ないです。コンピューターの数値積分を使っていけば線をずっと引いていけるのですが、紙の上で式として表せるケースというのはほとんどないので、実は紙の上で計算するという意味では使いづらい式になります。

ただ、コンピューターを使うと数値積分ができるので、この方程式を解いていくことによって電気力線を描くことができます。

そのようなことをやってるソフトウェアは「電磁界解析ソフトウェア」というのがあって、市販されているものがたくさんあります。

一直線上にある電荷による電気力線

それよりも、今からやるのは少し計算や少し使える方法です。

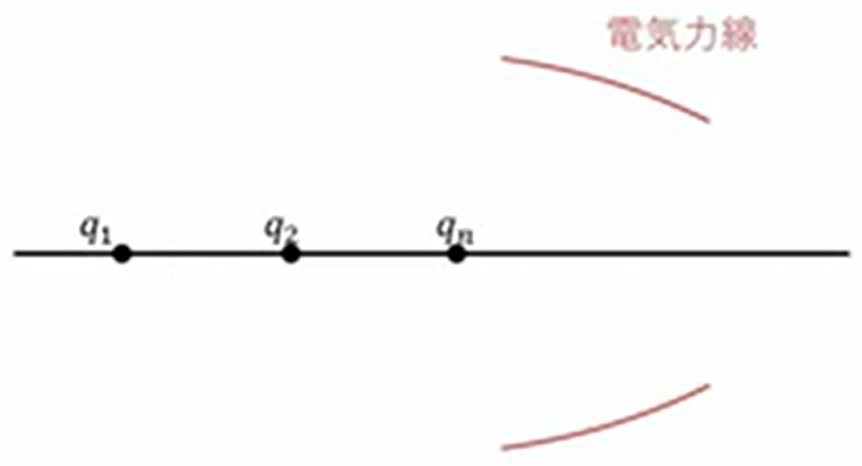
まず考えるのは、一直線上に電荷は\(q_1、q_2、…、q_n\)までがあります。

このように電気力線があった時にどう考えるのかということです。

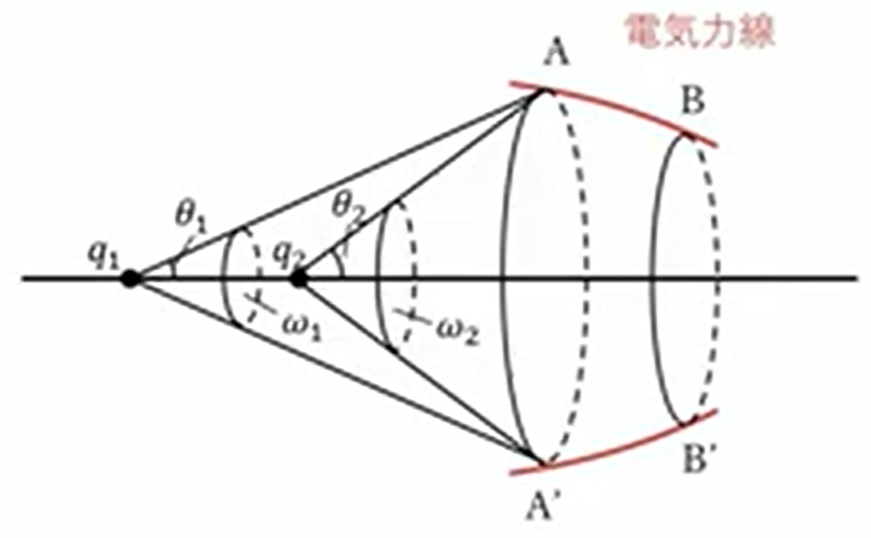
まずこれです。電気力線のある\(AA’\)を見た、円形を考えます。円形なので\(q_1\)から見てみると、ここを頂点とする円錐形になってるわけです。で、\(q_2\)から見るとこのような円錐形になっています。

そうすると、以前「立体角」というのを勉強をしましたが、円錐面の場合は半頂角を\(θ\)とすると、立体角は\(2π(1 \ – \ cos \ θ_1)\)で表されるということをやりました。

なのでこの場合、表す立体角\(q_1\)の円を見込む立体角というのは、\(i\)板面の電解に対して次のようになります。

\(ω_i = 2π(1 \ – \ cos \ θ_i )\)

そうすると、\(q_1\)から\(q_i\)という電気力線が出る（\(\frac{ε_0}{q_i}\)）わけですけれども、これは全方位に出ていきます。

で、そのうちに「\(AA’\)のこの面を通るのはいくつですか？」ということを考えると全方位を見渡した立体角は\(4π\)でした。なので\(4π\)のうちの\(ω_i\)の立体角分だけがここの面積を通るわけですから、出た電気力線の総数に4π分の立体角\(ω\)をかけたものということになります。

それにこの立体角の式を入れて計算するとこういうことになります。

\(\frac{q_i}{ε_0}\frac{ω_i}{4π}=\frac{q_i(1 \ – \ cos \ θ_i)}{2ε_0}\)

なので、これはこの\(q_i\)番目の電荷からこの断面積\(AA’\)を通る電気力線の数ということになります。

\(AA’\)を通る電気力線総数　\(\displaystyle \sum_{i=1}^{n} \frac{q_i(1 – \ cos \ θ_i)}{2ε_0}\)

そうすると、\(q_1\)から\(q_n\)までn個の電荷があるわけですから、同様にすると\(AA’\)を通る電気力線の総数は、それを全部足し算してあげればいいわけでして、このようになります。

\(\displaystyle \sum_{i=1}^{n} \frac{q_i(1 – \ cos \ θ_i)}{2ε_0}=\) 一定

そこで\(AA’\)に電気力線が通っていくわけなんですが、先ほどやったように電気力線は他の電気力線と交差することはありません。なので、この電気力線は外に出ていくことはできません。こちらはもう外に出ていくことができません。

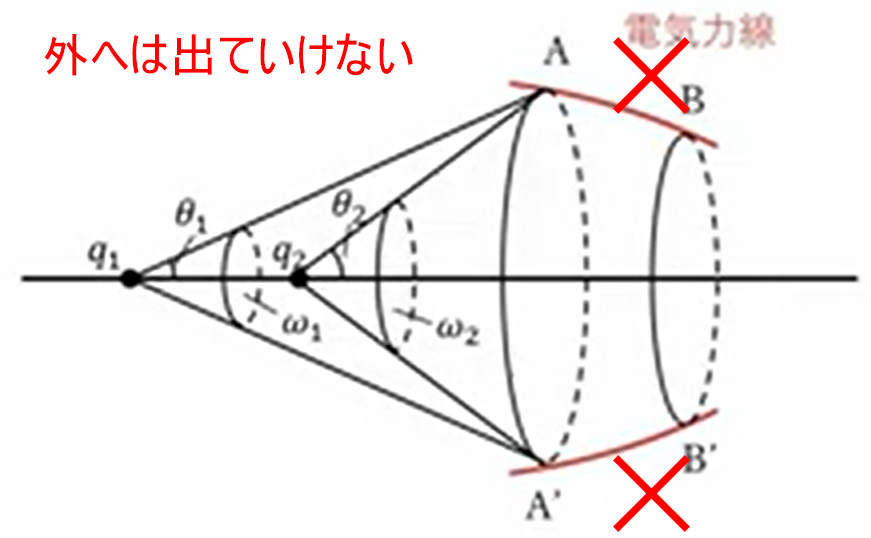
ということを考えると、\(AA’\)を通った電気力線は、\(BB’\)の面積、ここを必ず通らなきゃいけません。だから\(AA’\)を通る電気力線の本数と\(BB’\)を通る電気力線の本数は同じということになります。

なので、どこの点を取っていっても電気力線の本数\(\displaystyle \sum_{i=1}^{n} \frac{q_i( \ 1 – \ cos \ θ_i)}{2ε_0}\) が変わりませんよ、という性質になるわけです。

でそれをちょっと計算しますと、ここも\(q\)も与えられた電荷で一定値で、これを「真空の誘電率」で乗数ですので、この式が結局は\(q_i cos θ_i\)の、これを全部足したもの全電解に対して足したものが、電気力線のどの時点でとってもこれが「一定」とか「ありません」というような法則が成り立つわけです。

\(\displaystyle \sum_{i=1}^{n} qi \ cos \ θ_i \ = \)一定

で、先ほどの電気力線の方程式よりもこちらの方が電気力線のある点、ある意味で計算するのでいくつか使える場合があります。

なので「\(q_i \ cos \ θ_i\)のシグマが一定になるんですよ」っていうことですね。

例題

1つ例題をやってみたいと思います。

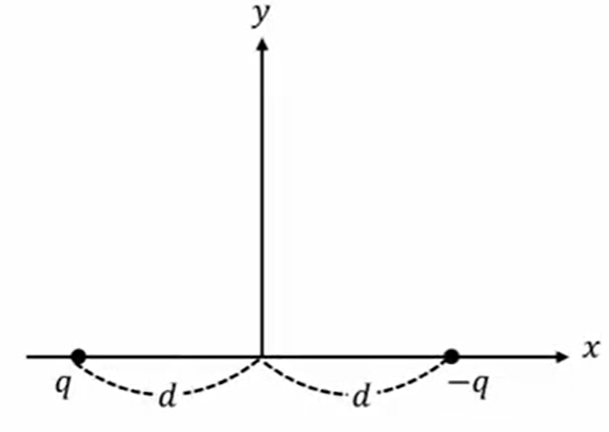
\(x-y\)平面で\(x\)軸上\((0, -d)\)、\((0, d)\)に\(+q\)、\(-q\)の二つの電荷があるときの電気力線の方程式を求めよ。

そうすると次のように、ある点\(xy\)という点での電気力線を考えるわけです。

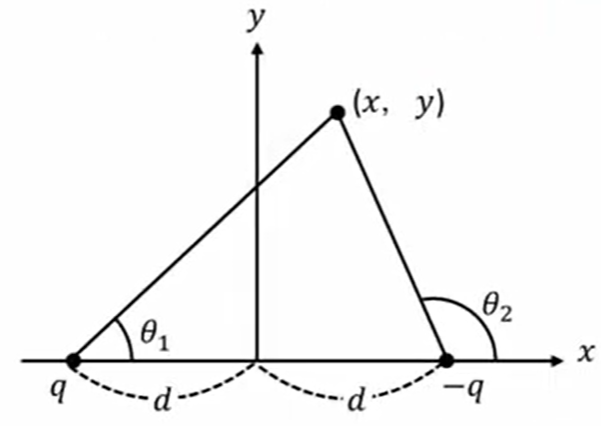
先ほどやったように「\(q \ cos \ θ\)はシグマが一定」ということがあったので、\(q\)の電荷からしてみれば、これは\(q \ cos \ θ_1\)と。

\(q\)の電荷はマイナスですので、それはここマイナスになりまして、ここ引いたとするとマイナスでございます。これが一定ですよということになります。

\(q \ cos \ θ_1 – q \ cos \ θ_2 =\) 一定

そうするとあとはもう幾何的に\(cos \ θ_1\)と\(cos \ θ_2\)を、三平方の定理を使ってこのように表せるわけです。

\(cos \ θ_1 = \frac{x+d}{\sqrt{{(x+d)}^2 + y^2}}\)　\(cos \ θ_2 = \frac{x-d}{\sqrt{{(x-d)}^2+y^2}}\)

これを代入してみますと、次のようになります。

\(q \ cos \ θ_1 \ – \ q \ cos \ θ_2 \ =\) に
\(cos \ θ_1 = \frac{x+d}{\sqrt{{(x+d)}^2 + y^2}}\)　\(cos \ θ_2 = \frac{x-d}{\sqrt{{(x-d)}^2+y^2}}\)をそれぞれ代入
\(q\frac{x+d}{\sqrt{{(x+d)}^2+y^2}}-q \frac{x-d}{\sqrt{{(x-d)}^2+y^2}} =\) 一定

そうすると\(q、q\)は一定値ですので、これをなくしてしまいまして、次のような形の式になります。

\(\frac{x+d}{\sqrt{{(x+d)}^2+y^2}} – \frac{x-d}{\sqrt{{(x-d)}^2+y^2}} =\) 一定

これがこの場合の電気力線の式です。

一定値ですので、ここの値をパラメーターとして変えていって電気力線をプロットしていくと、実際にコンピューターやエクセルなんか使ってやってみてもいいのですが、下図のように電気線がプロットできるということになります。

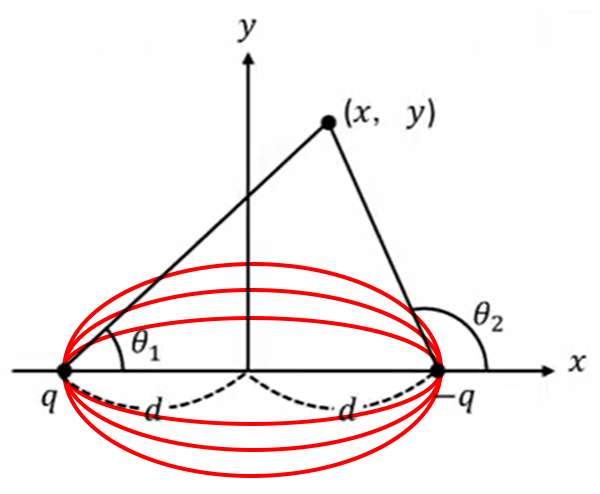
例題2

もう1つ例題です。

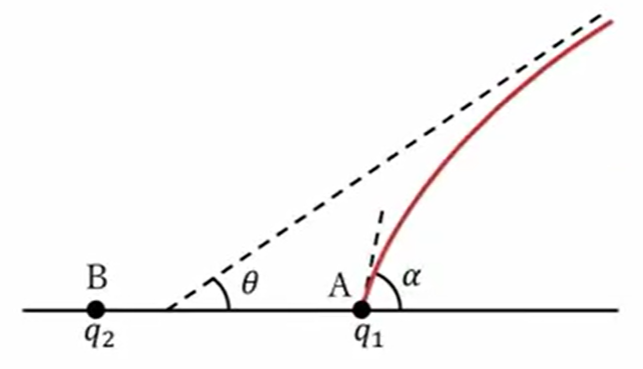
\(q_1、q_2\)の電荷が\(A、B\)にあるとき、\(A\)点から\(BA\)に対して\(α\)の角度で出る電気力線は、無限遠では\(BA\)に対してどのような角度になるか。

今度は2つの点が\(q_1\)、\(q_2\)がある場合を考えますと。

その時\(q_1\)から角度\(α\)で出る電気力線、この図では赤線で示していますけど、こんな電気力線があります。

角度\(α\)で出ていったこの電気力線は、無限遠に行った時に、この直線に対してどのような角度になりますか？という問題です。

それも先ほどの「\(q \ cos \ θ \)は一定」ということを使うと解くことができます。電気力線が出たところ、\(q_1\)の時点を考えますと、\(q_2\)から見るとこれは0ですね。だから\(θ_2\)は0です。

\(q_1\)から見ると\(α\)の角度が出ていくので、出たところで\(θ_1\)は\(α\)、\(θ_2\)は\(0\)ということです。

じゃあ無限遠に行ったところは、\(q_2\)から見ても\(q_1\)から見ても、この\(θ\)という角度になりますので、無限遠では\(θ_1\)も\(θ_2\)も\(θ\)ということになります。

なので、この出たところと無限遠で\(q \ cos \ θ_1\)を足し算したものが同じですよという式を立てます。

まず出たところでは、\(q_1 \ cos \ α \ + \ q_2 \ cos \ 0 \ = \ q_2 \ cos \ 0\)となります。そして無限遠では\(q_1 \ cosθ+q_2 \ cos \ θ\)、こういうことが成り立ってますよということです。

これから\(θ_1\)を求めてやればいいわけでして、これは単なる三角方程式になっているだけですので、あとは数学の問題になります。

計算をまとめると、次のような形になります。

A点を出たところでは、\(θ_1 = α、θ_2 = 0\)
無限遠では、\(θ_1 = θ_2 = θ\)
\(q_1 \ cos \ α \ + \ q_2 \ cos \ 0 \ = \ q_1 \ cos \ θ \ + \ q_2 \ cos \ θ\)
\(q_1 \ cos \ α \ + \ q_2 \ = \ (q_1 + q_2) \ cos \ θ\)

そこで「半角の公式」、高校の数学以来、使う機会が少ない方式かもしれませんが、\(cos \ θ\)と\(cos \ α\)のところに半角の公式を適用しますと、このような形に直すことができます。

\(q_1(1-2 \ sin^2 \ \frac{α}{2}) \ +q_2 \ = (q_1+q_2)(1-2 \ sin^2 \frac{θ}{2})\)

これをさらに計算進めていくと、

\(q_1 \ sin^2 \ \frac{α}{2} \ = \ (q_1 \ + q_2 \ )sin^2  \frac{θ}{2}\)

と計算できまして、これを直してやると

\(sin \frac{θ}{2}=\sqrt \frac{q_1}{q_1+q_2} sin \ \frac{α}{2}\)

となります。なので、これをθの形に直すと、次のような形になります。

\(θ \ = \ 2 \ con \ sin^{-1} (\sqrt \frac{q_1}{q_1+q_2} sin \ \frac{α}{2})\)

例題3

もう1つ例題です。

2個の電荷\(4q\)と\(-q\)があるとき、\(4q\)から出た電気力線の一部は\(-q\)に入り、その他は無限遠にいく。\(-q\)に入るものと入らないものとの境界電気力線は\(4q\)をどのような角度で出発するか。

電気力線の2個の電荷、\(+4q\)と\(-q\)がある場合ですね。そうすると、プラスから\(q\)なので、電気力線が1つは\(+4q\)から\(-q\)へ向かって入り、それがだんだん次のようになってきて、あるところの電気力線は無限大に行ってしまうことが想像できます。

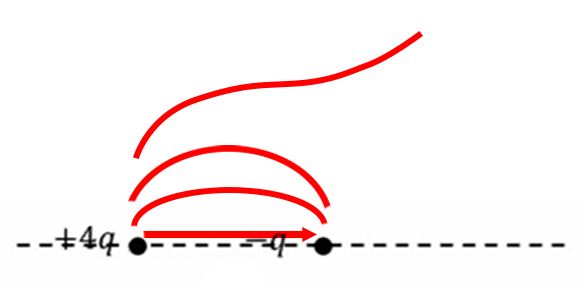
このように、\(+4q\)から出た一部のものは\(-q\)に入るのですが、それ以外のものは\(-q\)には入らずに無限遠に行ってしまいます。

\(-q\)に入るものと無限遠に行くもの、その境界となるのは、\(-q\)に入る線の角度が大きくなって、あるところまでいくと無限大に行ってしまうということが想像できるわけですが「その境界の角度というのはどれぐらいの角度なんですか？」という問題です。

そうすると、正確な図としては次のようになります。

まず\(θ\)を出た電気力線は\(θ_2\)です。ここから見た角度は\(π\)ということになります。あるところからは無限大に行ってしまうと。で、あるところから入ると。

で、ちょうどその境目のところが、グリーンで書いてある線です。電気力線としては下図の矢印のように来るので、ぶつかるところは実は特異点になるわけです。

なので、そうすると入る場合であっても無限大へ行く場合であっても、\(θ_1、θ_2\)、どちらから見た角度も\(0\)になるわけです。

なので、この2つについて「\(q \ cos \ θ\)が一定ですよ」っていう式を立ててあげます。

\(4q\)を\(θ_1\)で出るところで、\(θ_2 = π\)
\(-q\)に入るか、入らないかの境界線では、入っても無限遠にいっても\(θ_1 ≒ θ_2 ≒ 0\)
その境では、\(θ_1 \ = \ θ_2 \ = \ 0\)

そうすると、出たところでは\(4q \ cos \ θ_1\)で出ていくわけです。で、無限遠では角度は\(0, 0\)になってますので、式は

\(4q \ cos \ θ_1 – q \ cos \ π \ = \ 4q \ cos \ 0 \ – \ q \ cos \ 0\)

となり、これを計算していきます。\(q\)を全部消してしまいます。

\(4 \ cos \ θ_1 \ + \ 1 \ = \ 4-1\)
\(cos \ θ_1 \ = \ \frac{1}{2}\)

ということを三角関数の定義から\(θ_1\)っていうのは60°です。ということで、60°を境にして、60°より小さいものは全部\(-q\)に入ります。これより大きい角度で出ていったものは全部無限大に出ていきます。

以上、例題を見てみました。

おわりに

今回は、まず電気力線が「どういうものなのか」というのを学習して、それを用いて、電磁気学で前半の静電気のところでは重要な法則になる「Gaussの法則」の説明と、電気力線の例題を見てきました。

以上です。

江口先生の動画解説

はじめに：当記事は、動画で解説している内容をご紹介していますが、音声を流せる環境にある方はぜひ動画をご覧いただき、江口先生の授業の雰囲気も一緒に掴んでいただければと思います。

江口和弘講師：「【大学物理】電磁気学 第4回 – 電気力線とGaussの法則」（所要時間 29:05 ）