ブログ
BLOG
こんにちは。究進塾 編集部です。今回は、川崎医科大学附属高校の平成31年一般入試「理科」の第3問を解説です。
第3問の内容
問題は物理分野からの出題で「力学」に関する問題です。
問題
| 運動と力の関係を調べるために、次の【実験 1】【実験 2】を行った。100gの物体にはたらく重力の大きさは1Nであるとして、以下の問に答えなさい。
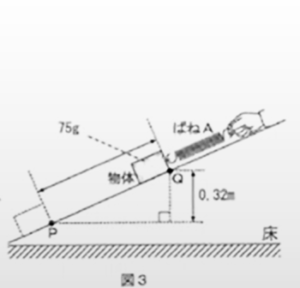
【実験 1】 図1のように、ばねAにおもりをつるして、ばねAの伸びを測定した。図2は、いろいろなおもりをつるして測定した結果をグラフにしたものである。 【実験 2】 図3のように、ばねAに質量75gの物体を取り付け、力のつり合いを保ちながら、物体を斜面に沿って点Pから点Qまで引き上げた。このとき、ばねAの伸びは常に4.8cmであった。 (1) 【実験 1】について、次の問いに答えなさい。 (2) 【実験 2】について、次の問いに答えなさい。
|
問題が長いので、(1)と(2)で分けて、順に解説します。ちなみに(1)は基礎レベルの問題で、(2)はやや難しい問題になっています。
(1)の解答
| (1) 【実験 1】について、次の問いに答えなさい。 ① おもりの質量とばねAの伸びには、どんな関係があるか。 ② おもりの質量が125gのとき、ばねAの伸びは何cmになるか。 ③ ばねAの伸びが4cmになるのは、おもりの質量が何gのときか、小数第1位を四捨五入して答えなさい。 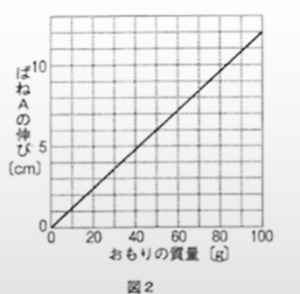 |
① おもりの質量とばねAの伸びには、どんな関係があるか。
ばねの重りの質量と、ばねAの伸びにはどんな関係があるかを考えますが、グラフを見れば一目瞭然です。
このグラフは、原点を通る直線になっています。ということは、ばねAの伸びと重りの質量の関係は原点を通る直線なので「比例関係にある」と。グラフを見れば、知らなくても一発で解答が分かるという問題です。
A. 比例関係
② おもりの質量が125gのとき、ばねAの伸びは何cmになるか。
比例関係にあるので、比例の式を求めてあげればいいわけです。質量をxとして、ばねの伸びをyとして式を作ってみます。表を見ると、おもりの質量の軸\(x\)が100いったところを見ると、ばねAの伸びの軸\(y\)は12上に登っているので、比例定数は\(\frac{12}{100}\)です。
なので、\(y\)と\(x\)の関係は、\(y=x\)というふうに求めることができます。この式ができれば簡単に求めることができます。
質量を\(x\)[g]、伸びを\(y\)[cm]とすると、\(y=\frac{12}{100}x\)
②は、重りの質量が125なので、\(x\)に125を入れて計算すれば、先ほどの式の\(x\)に125を入れて計算すると答えは出てきます。答えは15cmです。
A. 15 [cm]
③ ばねAの伸びが4cmになるのは、おもりの質量が何gのときか、小数第1位を四捨五入して答えなさい。
③は逆で、今度は伸びが4cmの時、重りの質量は何gかということです。これは、\(y\)のところに4を入れればいいわけなので、まずこの\(y=\frac{12}{100}x\)の式を、「\(x=\)~」の式に直して、\(y\)に4を代入します。そうすると33.3と答えが出てきます。
\(x=\frac{100}{12}×4=33.3\)
そして、「少数第1位を四捨五入して答えなさい」ということが書いてありますので、答えは33gとなります。
A. 33 [g]
| これは、ばねの伸びに関する非常に基礎的な問題です。 |
(2)の解答
こちらはやや難しい問題です。
| 【実験 2】 図3のように、ばねAに質量75gの物体を取り付け、力のつり合いを保ちながら、物体を斜面に沿って点Pから点Qまで引き上げた。このとき、ばねAの伸びは常に4.8cmであった。
(2) 【実験 2】について、次の問いに答えなさい。
|
① 物体を点Pから点Qへ引き上げるとき、ばねAが物体をひく力は何Nか。
先ほどの「100gの物体に働く重力の大きさが1N」ということで、ニュートンを換算してあげればいいわけです。なので、これも\(x\)を求めるので、
\(x=\frac{100}{12}×4.8\)cm
そうするとおもりは40g。(1)の実験で40gのおもりを下げた時と同じということです。そうすると100gが1Nなので、40gがぶら下がった時の重力の大きさは0.4Nになります。
\(x=\frac{100}{12}×4.8 = 40[g] =0.4[N]\)
A. 0.4[N]
② 斜面には摩擦があり、物体が斜面上を動いている間の摩擦力の大きさは0.1Nであった。PQ間の距離は何mか。
すぐ思いつくのは、坂道を上げる時に重力に逆らって上げたのと(右側の垂直矢印)、引き落とそうという力に逆って上げようとした時(左側の斜めの矢印)の仕事は同じですよ、っていうのが仕事の原理です。
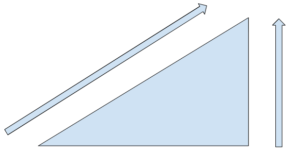
しかし、この問題を難しくしているのは、「摩擦力がある」ことです。摩擦力があると、仕事の原理は基本的に成り立ちません。なのでそこを考えなきゃいけないわけです。
①の答えで引いてる力は0.4Nということが出ています。また、摩擦力というのは「動かしてる方向と逆向きにはたらく」のが摩擦力、いわゆる抵抗力なので、この場合は斜面に沿って下向きに0.1Nという力が働いてます。
で今は、元々この物体を、重力が滑り落とそうとする力が働いていて、これが分からないわけです。そうすると、ここの釣り合いの式から考えて、0.4と0.1なので滑り落とそうとしてる力は0.3Nということが分かるわけです。
そうすると、この0.3Nに対して仕事の原理を使えば答えが出るわけです。
まず斜面に沿って上げようとすると摩擦がないと仮定して0.3×Lとします。で、75gの質量ですのでまっすぐ持ち上げようとすると0.75Nです。それと0.75Nで0.3に上がるわけですから、まっすぐ上げた場合は0.75×0.32。これは摩擦力を抜いて考えたので、ここでは仕事の原理が成り立ってるのでこれが等しいとおけます。
物体を滑り落そうとする力は\(f\)は、\(f=0.4-0.1=0.3\)[N]
よって、\(0.3×L=0.75×0.32\) (仕事の原理)
ここからLを計算すると、Lは0.8mと出ます。
\(L=\frac{0.75×0.32}{0.3}=0.8\)[m]
③ 物体を点Pから点Qに引き上げた後、点Qで静止させるとばねAの伸びが変化した。この時物体にはたらく摩擦力は斜面に沿って上向きに0.05Nであった。ばねAの伸びは何cmになるか。
静止してるわけですから力が釣り合っているわけなので、それを書いてあげます。まず今回バネの引く力を分からないのでFと置いておきます。
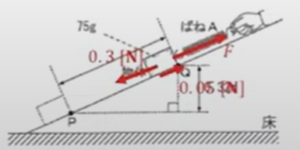
滑り落とそうとしている力は②で計算したので0.3Nです。
次に、摩擦力が0.05Nなんですが、問題文にあるように、この摩擦力は斜面に沿って上向きに働いているので、「この向きに0.05N」ということになります。そうするとこの3つの力が釣り合っているわけですから
\(F = 0.3-0.05 = 0.25\)N
ということが求められます。そして、その時の伸びを求めたいわけですから、重力0.25Nに換算して質量に直してあげると、25gをばねにぶら下げた時の伸びと同じ、ということになります。
なので①で一番最初に出した式に、xに25を入れてあげると、ばねの伸びyが計算できます。
\(y = \frac{12}{100} × 25 = 3\)[cm]
A. 3[cm]
| ポイント
後半はちょっと難しいのですが、何が難しくしてるかというと「摩擦がある」ところです。 まず摩擦力は物体が動いてる方向と必ず逆向きに働きます。そして摩擦があると、そのまま仕事の原理は成り立ちません。 ここが問題を難しくしている点です。 |
まとめ
以上、平成31年一般入試「理科」の第3問を見てきました。次回の川崎医科大学附属高校の入試対策は、「数学」の「関数(1次,2次)と図形」の過去問解説を掲載予定です。
川崎医科大学附属高校の入試対策
→【2025年版】川崎医科大学附属高校 数学 過去問解説|小問集合
| 講師:江口和弘
<経歴> 一般企業で研究職として活躍後に、塾講師へ転身しました。大学補習の物理系科目をメインに活躍しています。明るく親身な指導が特長で、これまで何人も単位取得に導いています。 |