こんにちは。究進塾 編集部です。今回は、川崎医科大学附属高校の入試対策について解説します。「令和2年一般入試」の「数学」第1問の解説です。

第1問の構成

川崎医科大学附属高校 令和2年 一般入試数学　第1問証文集合 (1) 根号の計算 (2)式の値 (3)因数分解 (4)場合の数と確率 (5)データの分析

上記のように、5問の小問からなる「小問集合」問題になっており、全てが基礎レベルの問題です。

これを順番に見ていきます。

(1)根号の計算

これは、間違えずに計算していけば確実に解答が出る、むしろ確実に正解して欲しい問題です。

あえて言うとポイントは、次の3点です。

・根号を含む計算をする時は、なるべくルートの中は小さい数になるように整理する
・割算が入っていたら分数で表す
・分母にルートが来たら有利化する

この辺りの3つが大きなポイントになります。なので、令和2年の問題を、これに従って計算していきます。

(1) √32-√6÷√3+\(\frac{6}{√2}\)=（　　　）

計算の手順
①「√32」は32×16なので、「4√2」というふうに、√の中を小さくすることができます。
②次の「√6÷√3」というところは、計算の順番から言って、+ – よりも先に計算するわけですが、そこを分数に置き換えてあげます。
③最後の√6のは、分母分子に√2をかけて有利化をしてあげます。

まずこれで整理して計算していくと、次のようになります。

=4√2-\(\frac{√6}{√3}\ + \frac{6}{√2}\ ・\frac{√2}{√2}\ \)

で、4√2はそのままで、分数になったところは√の中に\(\frac{3}{6}\)が入るのでここは√2になり、有理化したところは3√2なので、

=4√2-√2+3√2

このように√を含む分は√2のみになり、簡単に計算できます。

A.　6√2

計算問題というのは、入試問題で多く出るのですが、確実に、計算ミスなく計算して加点したいところです。

(2)式の値

(2) xの2次方程式 \({(2x-1)}^2 = (x-3)(3x-1)\)の解のうち、大きい方の解は\(x=\)（　　　　）

意味ありげに因数分解されるような形になってて「何か工夫ができるんじゃないのか」という形をしていますが、どうにもならないので基本これは展開して整理します。

計算の手順
①2次方程式は\(ax^2 + bx+c=0\)の形にする
②まず、因数分解できないかを考える
③因数分解できなければ解の公式を使う
\(x=\frac{-b±\sqrt{b^2-4ac}}{2a}\ \)

①に記載したように、2次方程式を解く時は「\(ax^2 + bx+c=0\)の形にする」というのが基本になりますので、1度その形に展開して計算することを考えます。

なので左辺は、2乗の展開を使い、右辺も展開の公式を使って、

\(4x^2-4x+1 = 3x^2 – 10x+3\)

そしてこれを全部左辺に移行します。

\(x^2+6x-2=0\)

解答のコツ このような2次方程式を解く前にまず考えるのは「因数分解できるかどうか」ということです。 なぜかというと、因数分解できると簡単に解を求められるので、まずは「因数分解できないか」ということを考えます。 できなければしょうがないので「解の公式を使う」という流れで解いていきます。 本問の場合、\(x+6x-2\)は因数分解できません。だから、しょうがないので解の公式を使います。 解の公式は、先述の「計算の手順」③にある\(x=\frac{-b±\sqrt{b^2-4ac}}{2a}\ \)です。非常に覚えにくい公式ですが、しっかり頭に入れて覚えておくようにしてください。

ではこの\(x^2+6x-2=0\)に解の公式を適用すると、aが1、bが6、cが-2になるので、次のように計算できます。

\(x=\frac{-6±\sqrt{6^2-4・1(-2)}}{2・1}=\frac{-6±\sqrt{44}}{2}=\frac{-6±2\sqrt{11}}{2} = -3±\sqrt{11}\)

\(3±\sqrt{11}\)というのが、この方程式の解になります。ただし、問われているのは「大きい方の解はいくつですか」ということですから、「-3+√11」と「-3-√11」では、当然「-3+√11」の方が大きいので、この場合の答えは「-3+√11」となります。

A.　-3+√11

(3)因数分解

\(x^2-4y^2\)を因数分解すると（　　）,　\(x^2-4y^2-2x+4y\)を因数分解すると（　　）, \(x=√5+√2\), \(y=\frac{√5-√2}{2}\)のとき\(x^2-4y^2-2x+4y\)の値は（　　）

これは色々に書いてあるんですが、順番にヒントというか、誘導されているような形になってます。

計算の手順
①\(A^2-B^2\)の形を見抜く
②式の値の計算は、いきなり代入せずに、ラクできないか考える

例えば、2番目の\(x^2-4y^2-2x+4y\)ですが、これを「因数分解しなさい」と言われると、中学生レベルではちょっと難易度が高い因数分解になります。なので、左にある\(x^2-4y^2\)を因数分解する、というところがヒントになるわけです。ですから、まずそこを見ていきましょう。

これのポイントは、\(4y^2\)が\(2y^2\)と見ることができるかどうか、ということです。ここはポイントになってきます。

そうすると\(a^2-b^2\)の形をしてるわけですから、簡単に因数分解できることは分かるわけです。このように\(a^2-b^2\)の形が含まれていることは多いので、この形が見抜けるようにしましょう。

これが4がなければ、例えば\(x^2-y^2\)だったら皆さん簡単に見つけるのですが、ここに数字が絡んでくると見つけられない人がちょこちょこ出てきます。なので数字が出てきた場合は、平方数を頭の隅に置いておくと、ここを見抜くことができます。平方数は、\(2^2=4、3^2=9、4^2=16、5^2=25\)、この辺りです。これを頭に置いておけば、簡単に因数分解することができます。

\(x^2-4y^2\ = (x+2y)(x-2y)\)

さて、このように因数分解できる形になったわけですから、2番目の\(x^2-4y^2-2x+4y\)の因数分解でこれを使ってみよう、というヒントになります。

そうすると、先ほどの前半の因数分解の形に置き換えてあげて、残った部分を2でくくってあげると共通要素の\(x-2y\)っていうのが見えてきます。なのでこれでくくって因数分解すると、次のようになります。

\(=(x-2y)(x+2y-2)\)

で、さらに最後は\(x=√5+√2\), \(y=\frac{√5-√2}{2}\)のとき\(x^2-4y^2-2x+4y\)の値はいくつですかという問題ですが、まさかこれをそのまま代入して計算しようということを出題者は意図していません。

なので、ここの\(x^2-4y^2-2x+4y\)の形はさっき因数分解した形になってますので、因数分解した\(=(x-2y)(x+2y-2)\)の形を使って簡単に計算できないか、ということを考えます。

まず\(x-2y\)を与えられたここから計算してあげますと2√2という非常に簡単な数値になってしまいます。

\(x-2y=√5+√2-2\frac{√5-√2}{2} = √5+√2-(√5-√2)=2√2\)

で、後半の\(x+2y-2\)も、計算していくと\(2√5-2\)というふうに簡単な数字になります。

\(x+2y-2=√5+√2+2\frac{√5-√2}{2}-2=√5+√2+(√5-√2)-2=2√5-2\)

そうすると、問題文にある「\(x^2-4y^2-2x+4y\)の値を求めろ」ということは、2番目で因数分解した「\((x+2y)(x-2y)\)の値を求める」ということと同じなので、結局「2√2と2√5-2を掛算すればでできますよ」ということになるので、これを計算すると「4√10 – 4√2」と簡単に計算することができます。

\(x^2-4y^2-2x+4y=(x-2y)(x+2y-2)=2√2(2√5-2)=4√10-4√2\)

A.　4√10-4√2

これを、与えられた式にそのまま代入してしまうと展開式をいっぱい使わなきゃいけなくなってしまって、ちょっと計算が大変になります。 計算はなるべく楽になるように工夫しましょう。

(4)場合の数と確率

Aさん、Bさん、Cさん、Dさんの4人が横一列に並ぶとき、並び方は全部で（　　）通りあり、そのうちＡさんがＢさんより左にいる確率は（　　）

これは基本的な順列、並び方の問題です。考え方は、Pを使うこともあるんですが、4箇所に並べればいいわけです。

〇1　〇2　〇3　〇4

そうすると、ここにはA、B、C、Dのどれかが入るわけだから、4通りあります。そうすると、〇1に1人入っちゃうと、〇2に入るのは〇に1入った人はもう入れないので、残りの3人から選ぶことになります。〇1と〇2で2人決まったので、〇3と〇4に入るのは、この2人以外の2人で、2通りあることになります。そして最後は1通りに決まります。

これを掛け算したのが「並び方の総数」というのが基本なので、これは結局24通りということになります。

4・3・2・1 = 24通り

A.　24通り

次に、後半の部分を解きます。「AさんがBさんより左にいる確率はいくつですか」という問題です。

全部で並び方が24通りあるわけですから、「AさんがBさんより左に来る並べ方」を考えればいいわけです。

最初はちょっと真面目にやってみます。この数え方ですが、4箇所に4人が入るわけですが、AさんとBさんが入る場所を決めてあげます。

●1　〇2　●3　〇4

ここにAさんとBさんが入るわけですから、もうこれを2箇所がAさん、Bさんが入る2箇所が決まればAさんが左に入るしかないわけですので、ひと通り決まってしまうわけです。

なのでまず「AさんとBさんが入る入り方は何通りあるのですか」というと、組み合わせです。4箇所から2箇所を選べばいいので、次のようになります。

\(\frac{4×3}{2×1}\)

これだけありますと。でAさん、Bさんが入る場所が決まったら、あとCさん、Dさんを並べればいいので

\(\frac{4×3}{2×1}×2×1\)

ということで計算できて、12通りということになります。

そうすると、全部の並び方が24通りあるので、確率は\(\frac{12}{24}\)で\(\frac{1}{2}\)ということになります。

\(\frac{4×3}{2×1}×2×1=12\)通り
よって確率は\(\frac{12}{24}= \frac{1}{2}\)

A.　\(\frac{1}{2}\)

実はこの問題は、ちょっと知恵使うと簡単にできまして、何も考えないと全部の並べ方24通りあるわけですが、この24通りは全て同様に確からしいわけです。で、そうすると並んだ時にAさんとBさんの関係は、AさんがBさんより左に来るか右に来るかのこの2通りしかないわけだから、当然半分になる。なので答えは1/2ですと、ちょっとスマートに答える解答の仕方もあります。

＜別解＞
4人並ぶ並び方のうち、AがBより左、またはAがBより右のどちらかなので、\(\frac{1}{2}\)

 

(5)データの分析

(5)下のグラフは、ある野球チーム37人の靴のサイズを表したものである。このデータの中央値は(　　)、最頻値は(　　)

解き方のポイント
データの代表値である、平均値、中央値、最頻値は押さえておく

中央値を求める

典型的なデータの分析、ヒストグラムの見方の問題です。まず中央値を求めます。中央値は小さい方から、あるいは大きい方からでもいいですが、並べて真ん中のデータが中央値です。

ここでは37人いるので、1人〜18人が並んで、19番目の人が来て、20番目〜37番目を並べます。

18人、18人と均等に並んで、19番目の人が中央値ということになります。

なので素直に数えていった方が早いのですが、

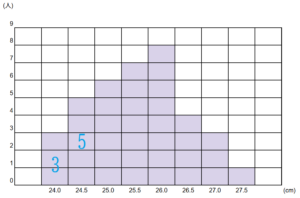
ここに3人、ここに5人いるので、これで小さい方から合計8人です。

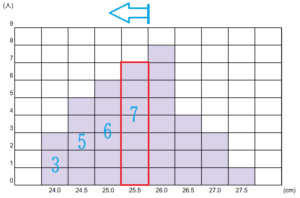
で、ここに6人いるので、ここまでで14人います。そうするとここには、7人いるので、ここまで以下で24人が入ることになるので、「19番目の人はここにいる」ということになります。

なので、中央値は25.5cmです。

A.　25.5cm

 

最頻値を求める

最頻値は「度数が最も多いデータ」のことを言います。そうすると、ヒストラムだとひと目で分かります。度数が1番多いところはもう見ただけで分かるので、最頻値は26.0cmということになります。

A.　26.0cm

データの分析では、よく出る代表値として、今回出ている「中央値」と「最頻値」の他にもう1つ「平均値」というのがあります。この3つは確実に計算できるように抑えておきましょう。 中央値に関して、今回の場合は37人だったので真ん中の人が存在したわけですが、これが例えば36人だった場合、真ん中の人がいないわけです。その場合、中央は「18番目の人と19番目の人」になります。 この場合の中央値の求め方はどうするのかというと、いないので、ここのデータ、18番目の人のデータと19番目の人のデータを平均値と取ります。 これも頭の隙に隅に置いておきましょう。

まとめ

以上、令和2年の一般入試数学 第1問の小問集合を見てきました。次回の川崎医科大学附属高校の入試対策は、「物理」の過去問解説「力学」について掲載予定です。

講師：江口和弘 ＜経歴＞ 東京農工大学工学部卒業 東京大学大学院工学系研究科修了 一般企業で研究職として活躍後に、塾講師へ転身しました。大学補習の物理系科目をメインに活躍しています。明るく親身な指導が特長で、これまで何人も単位取得に導いています。

動画版解説はこちら！