ブログ
BLOG
こんにちは。究進塾 編集部です。
今回は、久松先生の「線形代数 第3回」大学数学の線形代数の部分ベクトル空間の取り扱いについての解説です。
久松先生の動画解説
はじめに:当記事は、動画で解説をしている内容をご紹介していますが、音声を流せる環境にある方はぜひ動画をご覧いただき、久松先生の授業の雰囲気も一緒に掴んでいただければと思います。
動画紹介
【究進塾】大学補習チャンネル
【大学数学】線形代数 第3回 -部分ベクトル空間-(所要時間: 28分23秒)

東京工業大学卒業。東京工業大学大学院数学研究科博士課程修了。数学に特化した講師です。大学受験はもちろん、大学授業補習、大学院入試のサポートにも熟練しています。また、大学の情報系科目のサポートも経験があります。穏やかな性格と柔らかい雰囲気、丁寧な指導、そして数学愛が溢れる、おすすめ講師です。☆大学授業補習の詳細はこちら
部分ベクトル空間とは?
基本的には、部分ベクトル空間とは、まず、
| 条件①「あるベクトル空間の部分集合」(=ベクトル空間の一部分) 条件②さらに「その部分集合それ自身が、単体でベクトル空間になる」もの |
この2つの条件を満たすものを部分ベクトル空間と呼びます。
正式な定義は省きますが、以下のように定義してあることが普通です。
| 注)部分ベクトル空間は元のベクトル空間の算法を引き継ぐものとする |
「ある部分ベクトル空間」と言う場合、そこに定義されている算法は、加法(和)とスカラー倍というのが算法として定義されているはずですが、その算法は「元のベクトル空間の算法を引き継ぐものとする」と定義してあるのが普通です。
「部分集合に元の空間とは全く別の計算を導入した」というのは、一応それでベクトル空間になることはあるかもしれないですが、それは条件①の「元の空間の一部分である」という性質をあんまり反映してくれないので、通常「部分ベクトル空間」という場合は「元のベクトル空間の算法を引き継いで、元のベクトル空間の算法を使った時に、その部分集合自体がベクトル空間になるもの」と定義してあります。
このように抽象的な言葉を聞いてもよくわからないと思いますので、具体例をあたってみましょう。
| 例①:3次元実空間\(R^3\)の原点を通る平面 \(x+2y-3z=0\) |
「3次元実空間\(R^3\)」、これは普通のいわゆる空間ベクトルというやつです。3個成分があるもの(実数3つ組)です。
この式を満たすような\(R^3\)の中の平面になるはずです。これは部分集合になっているわけです。
実は「この集合上にある点の集まり」というのが、普通に\(R^3\)をベクトル空間とみなした時に、その算法を引き継いでいた時、この平面の中にのっているものは、この算法の中でやはりベクトル空間を成す、ということが言えたりします。(それについての証明は後述します。)
| 例②:4次元実空間内の2つのベクトル空間
\(x+y+z+w=0\) ←ベクトル空間① |
4次元実空間は\(R^4\)と表します。この中の2つのベクトル空間を用意します。
このそれぞれが、実は「4次元実空間内でそれぞれ部分ベクトル空間になる」と証明できるのですが、「それらの共通部分(=どちらにも入っているところ)だけを考えたものが部分ベクトル空間になる」となります。
絵で見るとわかりやすいと思いますが、4次元は絵に起こせないので、例①を図式すると次のようになります。
このような3次元空間のあったときの、式 \(x+2y-3z=0\)、これが平面を表す方程式だという事は、何となくわかると思います。ついでに言うとこれは「\(x=0\), \(y=0\), \(z=0\)」と入れたとき、ちゃんと左辺が0になるから右辺と等しい」となるので、原点を通っています。
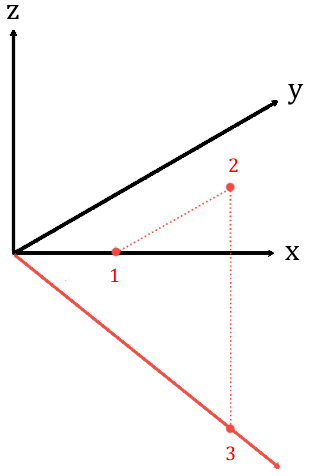
さらに言うと、1、2、-3 というベクトルと垂直になっているということもわかるはずです。なので、1、2、-3というベクトルを図式してみると、このような「原点を通って垂直になっているような平面」となるので、おおよそ以下のようになります。
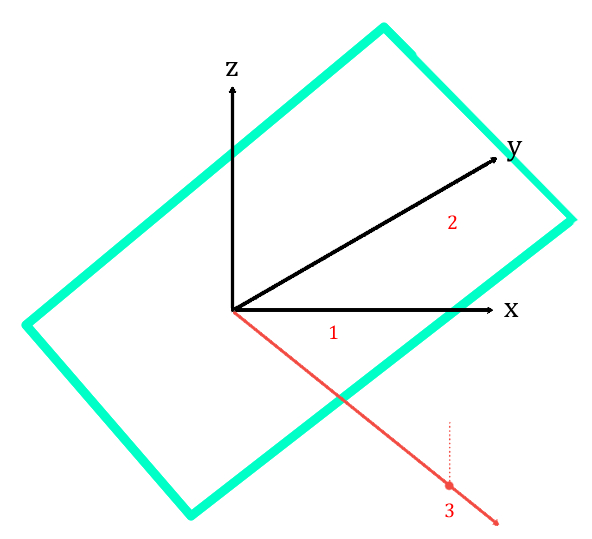
平面上に乗ってる点、全体というのが「部分ベクトル空間」ということがわかったりします。
とりあえず部分ベクトル空間というのは、
| ・足し算した時に、今考えている空間からはみ出ない ・実数倍した時に、今考えている空間からはみ出ない |
という性質を持っていないといけません。
実は、ある空間において、原点を通る平べったい形(まっすぐ、曲がってなさそうな形)というのは、大体部分ベクトル空間だったりします。
その一方で、ベクトル空間というものの性質として
| 「0を含んでないといけない」 「0ベクトルというものがあって」 |
と定義されているので、同じ平面でも減点を通っていないようなものは、一般には部分ベクトル空間とはなりません。
部分ベクトル空間になることの証明
線形代数の講義、演習、試験などでよく出るかもしれないのが、次のようなものです。
| 「ある定義された部分集合が、元のベクトル空間の部分ベクトル空間である、ということを示しなさい」 |
これは「直感的にはわかるけど、どうやって証明したらいいのかが、意外とわかりづらい」という人が多かったりします。
なので、ここで実例として「部分ベクトル空間である」ということを示すには、どんな手順で何をやったらいいのか、ということを紹介しておきます。
| ベクトル空間\(V\)の部分集合\(U\)が部分ベクトル空間であることを証明するには
i ) \(u_1\)、\(u_2∈U\) に対し、\(u_1+u_2∈U\) であること の2つが言えればよい。 |
ベクトル空間\(V\)は、つまり元の入れ物の空間です。
i)の解説
\(U\)に入っているベクトル2つ、\(u_1\)、\(u_2\) を持ってきます。\(V\)の部分集合であるということは、これらはベクトルになっているわけです。ベクトルなので和が定義されています。このとき、\(u_1\)と\(u_2\)を足したもの、\(u_1 + u_2\)がやはり\(U\)の中に入っていることを示す必要があります。つまり、足し算をした計算結果が部分集合\(U\)からはみ出ないということです。
これを、数学では「部分集合\(U\)が加法について閉じている」と言います。
ii)の解説
\(U\)のベクトル\(u_2\)と、任意の実数\(k\)(※今は実ベクトル空間を想定しているので、一応実数としておきます)に対し、
\(k\)倍の\(u\)(これも実数倍であることが定義されています)が、i)と同様に、やはり元の部分集合\(U\)からはみでないということです。
i) と ii) の2つが証明できれば良いです。
これが「部分集合\(U\)が、\(v\)の部分ベクトル空間になっている」ということの定義です。
では実際にこれを証明しようといった時に何をやればいいのか、ということを、先程の例を使って説明していきます。
| 例) 3次元実空間\(R^3\)の原点を通る平面 \(x+2y-3z=0\) が部分ベクトル空間であること |
これを証明します。
証明の手順としては、先程の i) と ii) がどちらも成り立つということを言えれば、それでおしまい、ということになります。なのでまず最初にやることは、今考えている点から2つの集合を取ってきたときに「これらを足し算したものがやはりこの集合に入っている」ということを、まずは最初に示すことになります。
というわけで、この平面から勝手な2点をとりあえず取ってきます。
座標 \(
\left(
\begin{array}{crl}
a\\
b\\
c
\end{array}
\right)\)\(
\left(
\begin{array}{crl}
p\\
q\\
r
\end{array}
\right)\) とします。
すると、この2点はこの平面上から取ってきた、つまりこの平面上に乗っているので、\(x+2y-3z=0\) の式を満たす必要があります。
ということはこの\(
\left(
\begin{array}{crl}
a\\
b\\
c
\end{array}
\right)\)\(
\left(
\begin{array}{crl}
p\\
q\\
r
\end{array}
\right)\) によって、それぞれ次のような式を満たすはずです。
\(a+2b-3c=0\)
\(p+2q-3r=0\)
このとき、この2点の(\(R^3\)としての)和というのを考えます。
\(R^3\)の部分ベクトル空間になることを示しましょう、と言っているので、「\(R^3\)をベクトル空間として見た時の算法として和を取る」というふうに考えます。
\(R^3\)のベクトル空間としての和というのは、普通に成分同士を足したもので、下記のようなものです。
\((a+p, b+q, c+r )\)
今から示すことは、この点が平面 \(x+2y-3z=0\)の平面状にちゃんと乗っているかということを、確認しなければなりません。
というわけで代入してみましょう。順に代入していくと、このような式になります。
\((a+p)+2(b+q)-3(c+r)\)
これは普通の足し算の分配法則や順序の並べ替えなどをやると、
\(a+2b-3c+p+2q-3r\)
となります。そしてこれは、\(a+2b-3c=0\) と \(p+2q-3r=0\) の条件があるので、上の式の前半と後半は、それぞれ0になります。というわけでこの式は、
\(0+0\)となり、当然0となります。このようなことがわかりました。
つまりどういうことかというと、点\((a+p, b+q, c+r)\) という点は、この平面を定義している方程式を満たしているので、つまりこの平面上に乗っているということがわかります。
これで2つある条件のうちの i) の方が証明できました。
あともう1つです。一般にはこちらの方が簡単な場合が多いです。「実数倍したものが、ちゃんとやはり同じ平面上に乗るか」という話です。
とりあえず、平面上の点から勝手なベクトルを持ってきます。先程と同じものを流用して\(a, b, c\) とします。これの実数倍\(ka, kb, kc\) というのを考えます。\(R^3\)のスカラー倍というのは、やはりこれも簡単に出来ていて「それぞれの成分をk倍する」という算法でした。
さてこうしてできた、この\(ka, kb, kc\) というのが、さっきの平面に乗っているかどうか、という話ですが、\(x+2y-3z=0\)を満たすかどうか、ということです。
それぞれの成分に代入してみます。
\((ka)+2(kb)-3(kc)\)
この式が0になれば、ちゃんとこの点が平面に乗っている、ということになります。これを\(k\)で括ってあげると、こんな式になります。
\(k(a+2b-3c)=0\)
そして元の\((a, b, c)\)が平面上の点だということがわかるので、0になります。ということは、この式というのは0倍の\(k\)となり「\(=0\)」となります。
したがって、点\((ka, kb, kc)\) はやはり平面上に乗っていることがわかります。
| 以上により、条件 i) ii) を共に満たすことがわかったので、平面 \(x+2y-3z=0\) は3次元実空間\(R^3\)の部分ベクトル空間である。 |
というふうなことが言えました。
証明の手順としては、大体流れがこのようになります。
で、これの最初「あるベクトル空間\(V\)の部分集合\(U\)が、部分ベクトル空間になっている」ということを証明するためには、この i) ii) の2つを示せば良いということで、この部分についてはきちんと覚えておく必要があります。
つまりこの2つが言っているのは、
「ちゃんと\(U\)がベクトル空間として機能している」
これが成り立ちさえすれば、
「\(U\)はちゃんとベクトル空間として存在できる」
ということになるので、そのことを調べていますよ、というものです。慣れるまでは、「こうやって証明するものだ」というのをよく覚えておくのが良いのではないか、と思います。
ベクトル空間の共通部分
もう1つのトピックです。最初に2つ挙げましたが、2つ目の方の例を解説します。
| 4次元実空間内の2つのベクトル空間、\(x+y+z+w=0\) と、\(2x-y-3z+w=0\) の共通部分 |
「上記の式、左側と右側との共通部分が、やはり4次元実空間内の部分ベクトル空間になる」ということです。これの構造がどうなるか、これが部分ベクトル空間であるかどうかということについては、先程の例をもとにして、試しに自分で確かめてみてください。ちょうど良い練習になると思います。
ここでは、この2つのベクトル空間の共通部分というのはどんな空間になるかを知るための方法を紹介します。
右の式も左の式も、1つの方程式で定義された3次元の超平面になっているのですが、方程式で書いてあればやることは結構簡単だったりします。(ベクトル空間を定義する方法としては、基底を指定する方法など、その他にもいくつか色々とあったりします。)
さて、考えるにあたって名前がないと不便なので、\(x+y+z+w=0\) を満たすようなベクトル全体の集まりを” \(U\) ” と名付けておきます。そうすると、” \(U\) ” というのはどんな集合になるのかというと、
\(\left (
\begin{array}{crl}
x\\
y\\
z\\
w
\end{array}
\right)
∈R^4\)
こういう四次元ベクトルです。\(x\)、\(y\)、\(z\)、\(w\) の間に、\(x+y+z+w=0\) の関係式が成り立っているようなものが全体となっています。
\(U =\) { \((x,y,z,w) ∈ R^4 | x+y+z+w=0\) }
同様に、\(2x-y+3z+w=0\)の式を満たすものを ” \(V\) ” と定義しておきます。
そうすると、これもやはり\(R^4\)の部分集合、実数4つ組(\(x\)、\(y\)、\(z\)、\(w\))で書けるわけですが、この\(x\)、\(y\)、\(z\)、\(w\)は、勝手な数字で良いわけではなく、「\(2x-y+3z+w=0\)を満たす数に限る」というわけです。
\(V =\) { \((x, y, z, w) ∈R^4 | 2x-y+3z+w=0 \) }
さて、というわけで2つの部分ベクトル空間はそれぞれ “\(U\)” と “\(V\)” と、このように定義できるわけですが、このとき、この2つの共通部分「\(U∩V\)」は、ちょっと考えれば当たり前だなと思うものではありますが、次のように定義できるわけです。
\(U∩V =\) { \(( x, y, z, w ) ∈R^4\) | \(\begin{array}{l} x +y +z +w = 0\\ 2x -y +3z +w = 0\end{array}\) }
\(U\)にも\(V\)にも入っている、つまり\(U\)の式と\(V\)の式両方を満たさないといけない、ということになるわけです。
というわけで、「\(U∩V\)」は4次元ベクトル空間内の点で、この2つの方程式を満たすもの、と表すことが出来ます。
これは「方程式で定義されている場合」の話になっていますが、基底で書いてあったとしても成分表示したとすると、結局、ほとんど全て数ベクトル空間の話に置き換えたりすることができるので、ここは誤解を恐れずに言ってしまえば、
| ベクトル空間の共通部分⇒本質的に連立方程式の解空間 |
2つの式(\(x+y+z+w=0\) と \(2x-y+3z+w=0\))を両方満たす全体の集まり(\(x,y,z,w\))が、共通部分(\(U∩V\))、というふうになっています。
考え方としては、これでほとんど十分だったりします。
ベクトル空間の共通部分の基底
実際に、その空間がどんなものになるかということを、今回は「基底を求める」という方法で調べます。
\(U∩V =\) { \(( x, y, z, w ) ∈R^4\) | \(\begin{array}{l} x +y +z +w = 0\\ 2x -y +3z +w = 0\end{array}\) }
「\(U∩V\)」が右の式で表されるような空間になっていました。すると、結局\(x\)、\(y\)、\(z\)、\(w\)がどんなものかというのは、右側の連立方程式を解けばわかるのでは、ということになります。
連立方程式の解き方については、以前ご紹介しているのですが、今回の式は簡単なので、そこまでしなくても高校の時にやっていたのと同じ方法で解いていいという感じです。
解いてみると、次のようになります。
| \(x=- \frac{4}{3}z – \frac{2}{3}w\) \(y=-\frac{1}{3}z – \frac{1}{3}w\) |
このようになると、ちょうど連立方程式の両方の式とも満たせるようになるだろう、というふうになっています。
つまりどういうことかというと、\(x\)と\(y\)というのは、実は勝手な数字が決められなくて、「\(z\)と\(w\)を決めるとそれを使ってこう書けるような数字じゃないといけませんよ」ということになるわけです。
そのことを考えて式を書いておくと、\(U∩V\)というのは
\(U∩V =\) { \(( -\frac{4}{3}z-\frac{2}{3}w, \frac{1}{3}z-\frac{1}{3}w, z, w ) ∈R^4 \) | \(z,w,∈R\) }
「\(z\)と\(w\)は実数になってもいいよ」という感じです。これを書き直すと、
①\(z\)がかかっている部分
②\(w\)がかかっている部分
というように、2つに切り分けます。
\(=\) { \(z (-\frac{4}{3}, \frac{1}{3}, 1,0) + w(-\frac{2}{3}, -\frac{1}{3}, 0,1) ∈R^4 \) | \(z,w,∈R\) }
このようになると、結局()内に入っている数字は、\(-\frac{4}{3}\)、\(\frac{1}{3}\)、1、0というベクトルの\(z\)倍と、\(-\frac{2}{3}\)、\(-\frac{1}{3}\)、0、1というベクトルの\(w\)倍を足したもの、そして\(z\)と\(w\)は実数なら何でもいい、ということになるわけです。
ということで、\(U\)と\(V\)というのはこの2つのベクトルがあればそれで定数倍したものの和、のようなもので表せるというようになっています。
そして、\(z (-\frac{4}{3}, \frac{1}{3}, 1,0) \)と\( w(-\frac{2}{3}, -\frac{1}{3}, 0,1)\)の2つを\(U∩V\)という部分ベクトル空間の基底、と呼んだりします。基底の定義については、次回以降に解説する予定ですが、今は「そのベクトル空間を表すのに必要な基本パーツ」くらいに思っておいてください。
| よって、\(U∩V\)の基底)(のうちの1組)は、
\( ※基底の取り方は他にもたくさんあります。「無数にある基底の取り方のうちの1組」という意味です。 |
左側の分数の式でも大丈夫ではありますが、きれいではないので整えました。\(z\)と\(w\)が「実数なら何でも良い」ので、左を3倍、右を\(\frac{1}{3}\)にするという対処法、()内がきれいになるような実数の取り方をすることができます。
で、「あるベクトルが基底になっている」となったとして、その基底にそれぞれ適当な0でない定数倍したものを集めてきたものも、やはりまた基底になる、ということが知られています。
なので、3倍、\(\frac{1}{3}\)倍すると、少しきれいな形になり、\(
\left(
\begin{array}{crl}
-4\\
1\\
3\\
0\end{array}
\right)\)と\(
\left(
\begin{array}{crl}
-2\\
-1\\
0\\
3\
\end{array}
\right)\)の2つのベクトルがあれば、\(U∩V\)という部分ベクトル空間は全て、この2つのベクトルの線形結合(実数倍して足し合わせたようなもの)で書ける、ということがわかります。
そうすると、ベクトル空間をちょっと知っている人だと、このことからさらに\(U∩V\)という空間の次元は「2次元だ」ということがわかったりするわけです。
というわけで、基底が解ってしまいさえすれば、一応そのベクトル空間についてはほとんどのことがわかるのではと、少なくとも書き表すのにそんなに苦労はしなくなるというのがあるので、こうして基底を求めておくと、\(U∩V\)の元を何か持ってきたり、あるベクトルが\(U∩V\)に入っているかいないかとか(入っているかいないかを判定するのは元の方程式に代入してみるというだけで別にいいと思うのですが)、次元をを求めるという話も聞かれたりするので、その時に基底を表す、実際に基底を持ってきてみる、のようなことをするのは、一応有効な方法ではないかと思います。
おわりに
今回は、線形代数の解説、部分ベクトル空間についてのお話でした。
最後に、究進塾では大学授業補習、大学院入試対策の講義も行っております。ご興味がある方は「無料体験授業をご希望の方」からお気軽にお問い合わせください。
究進塾 編集部

究進塾は、「学問の楽しさを伝え、結果を出す喜びを体験してもらうことで塾生の人生を豊かにしたい」という考えから、学習に役立つ情報や学習のコツなどを発信しています。
マンツーマン個別指導専門で、大学入試や大学院入試、単位取得、日大基礎学力テスト対策など、多様なニーズに対応。








