こんにちは。究進塾 編集部です。

電磁気学の第5回目です。前回はガウスの法則を学習しましたが、今回は「ガウスの法則を用いて電場をどう計算しているのか」というのを、基本的な電荷配置について見ていきたいと思います。

ガウスの法則を用いた電場計算、いわゆる「ガウスの法則の使い方」を、代表的な電荷配置について見ていきたいと思います。それをやる前に、まず前回やった「ガウスの法則」のおさらいをしておきましょう。

ガウスの法則（おさらい）

積分型 \(\displaystyle \int_{S}  E・dS \ = \ \displaystyle \int_{V} \frac{ρ}{ε_0} dv\) \((\displaystyle \int_ S D・dS \ = \ \displaystyle \int_{V} \ ρdv)\) 微分型 \(∇E \ = \frac{ρ}{ε_0}\) \((∇D \ = ρ)\)

ここに書いてますようにガウスの法則は「積分型」「微分型」の2つの形で表されて、各々このような形で表せます、というのが前回やったガウスの法則の学習でした。

今回は、主にガウスの計算の「積分型」を使用していくことになります。

導体

その前に、まず「導体」というのをやっておきたいのですが、導体は第1回でもやってますが、復習の意味で「導体とは何なのか」という話をしておきます。

導体とは「電気をよく通す物質」のことです。「電気を通す」というのは、電気は何を運ぶのかというと「導体の中にはたくさんの自由電子があるんですよ」という話を1回目にしました。このような物質のことを言います。

具体的にはほとんどが「金属」です。銅とかアルミニウム、鉄などの金属が導体に属します。これは第1回でもやったのですが、導体の性質として、

・導体の内部には電場はない（電場は0）

という、これが大事な性質になります。なぜかというと、もし導体内に電場があったとすると、それに向かって自由に動ける電子が直ちに動いちゃうわけですね。

そうすると、その動いた電子が電場と逆方向の電場を作るのでこれが電場が0になったところで落ち着いてしまう。

ということで、導体の中には電場は存在しません。電場はゼロです。これが重要な性質になります。

そうすると、電場がないわけですから、「導体内の電場がない」ということは、つまり導体内では電位はどこでも一定＝「等電位」です。こういうことになるわけです。

そうすると、もう1つは導体表面の電場の方向は、プラス電荷の場合、導体の表面に垂直で外向きです。（マイナスの場合はその逆です。）

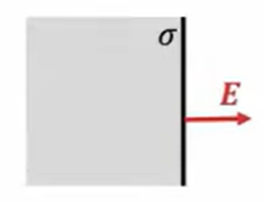
なぜかというと、導体がどの部分でも電位が同じだと先ほど説明しましたが、というとこれは表面でも同じで、ここの表面の部分では同じ電位になります。

ということは、「電位の傾き＝電場」なので、図の矢印と逆方向の電場はありません。電場は表面に対し垂直に向きます。

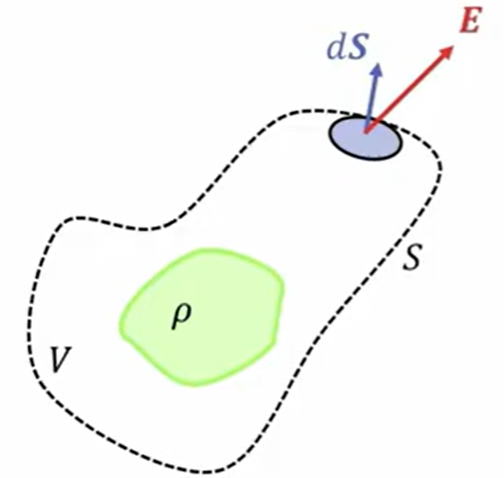
この電場の大きさですが、下図の破線で書いた部分に「ガウスの法則」を早速適用します。

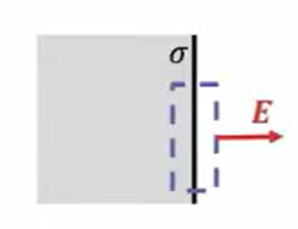
この断面積を\(dS\)としておきます。中にある電荷は、面だけに電荷が存在するわけですから、\(σdS\)という電荷が存在します。

そうするとガウスの定理を適用すると、破線の中にあるのが総電荷量です。そして導体の場合は、電場ゼロなので片側からしか出ていきません。

ということは出ていく面積は\(dS\)なので\(EdS\)ということになります。なのでこの場合、ガウスの法則を適用するとこのような式になります。

\(EdS \ = \frac{σdS}{ε_0}\)

これで\(dS\)を相殺して\(E\)に直してやると、電場の大きさは\(\frac{σ}{ε_0}\)となります。これが、金属表面に\(σ\)の綿密度で電荷が分布している場合の、導体の電場の大きさということになります。

導体表面にはたらく（静電）力

金属の表面っていうのは力がはたらくのですが、じゃあその力のはたらきはどうなるのですかっていう話をしたいと思います。

これは、意外と教科書にサラッと式が書いてあることが多いんですが「なんでそうなるの？」という説明は抜けてる場合がほとんどなので、それを説明したいと思います。

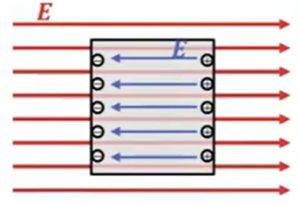
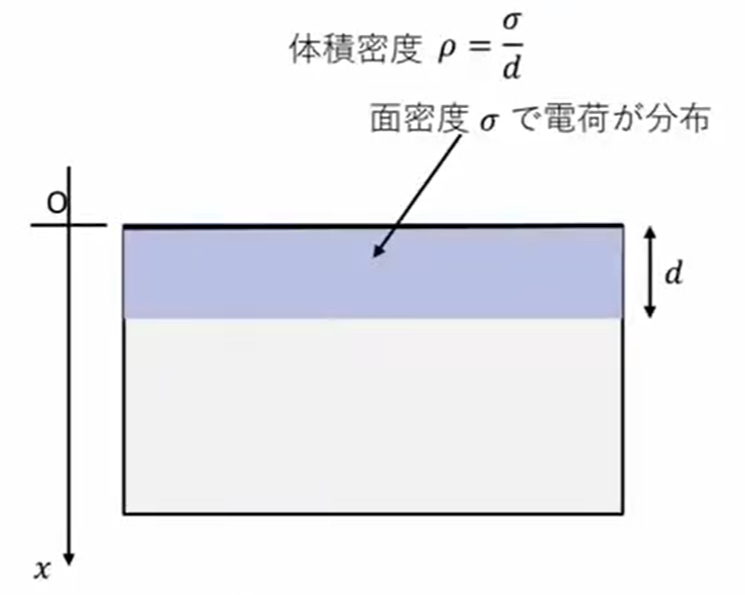
どう考えるのかというと、「電荷は金属の内部では表面だけに存在するんですよ」ということを言ったのですが、実際は、非常に微小な厚み\(d\)の中に電場が存在すると仮定します。

具体的に考えても、表面だけに存在してるって言っても電子はそもそも原子に属していたものですから、原子のサイズ、オングストローム単位のサイズのところの範囲を持っているところというふうになります。\(10^{-10}\)mぐらいのサイズです。

それぐらいの範囲には分布しているということも考えられるわけで、それを\(d\)と置いて、ここに面密度\(σ\)の電荷があるということに考えます。

そうすると、面密度を\(σ\)だとすると、厚さ\(d\)で体積密度に換算すると、体積密度は\(\frac{σ}{d}\)と、図のように水色で書いてある領域に電荷が均等に分布してるっていうことを仮定します。

これにガウス法則を適用するわけですが、ここで書いた赤の点線の領域、閉曲面にガウスの定理を適用します。

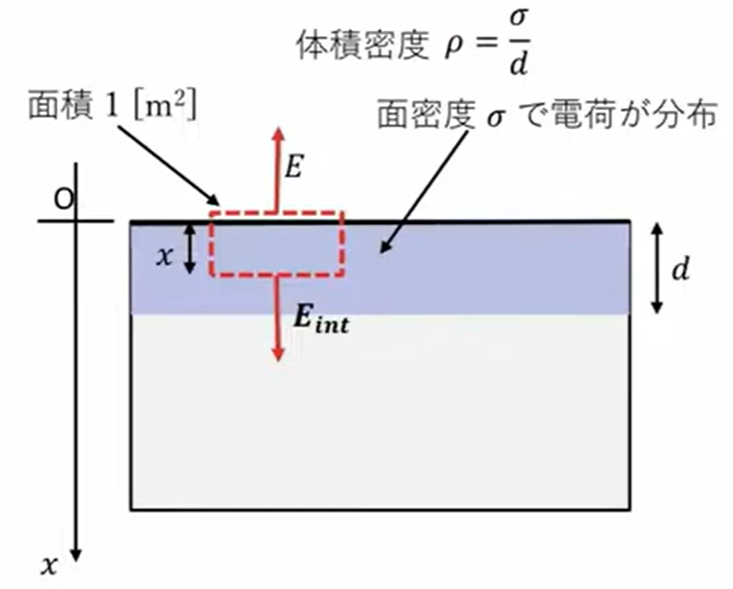
この場合は、断面積を1平方メートルと仮定しておきます。そうするとまず右辺はこの中にある総電荷量になりますから、厚み\(x\)を考えていますので、このところにある総電荷量は\(\frac{ρx}{ε_0}\)ということになります。

じゃあ出ていく電荷は外向きには\(E\)で、断面積が1です。内向きが当然これ外と内は違いますので、真空と物質があるところで違いますので、\(E_{int}\)としていますけど、\(E_{int}\)に断面積を掛けたものが出ていく電気力線の総数ということになります。

\(E・1 \ + \ E_{int}・1 \ = \ \frac{ρx}{ε_0}\)

これがガウスの法則を適用したところです。

そうすると、先ほど金属の表面では電場は「\(\frac{σ}{ε_0}\)ですよ」っていうのを、さっき導出したわけですが、これをこの式を使って体積密度に直してみると、外向きの電場Eは\(\frac{ρ}{ε_0}\)ということになります。

\(E \ = \ \frac{σ}{ε_0} \ = \ \frac{ρd}{ε_0}\)

これを代入して内向きの電場\(E_{int}\)というのを求めてみますと、\(E_{int}\)はこのような形になります。

\(E_{int} \ = \ \frac{ρx}{ε_0} \ – \ \frac{ρd}{ε_0}\)

そうすると、電荷\(q\)に働く力は\(q\)と\(E\)をかけ算したものでしたので、電荷があるところには\(E_{int}\)という電場が働いてるわけです。

だからこれをかけ算したものが働く力になるわけでして、これを\(x\)を\(0\)から\(t\)まで足し算（積分）してやると「働く力の総量」ということになります。

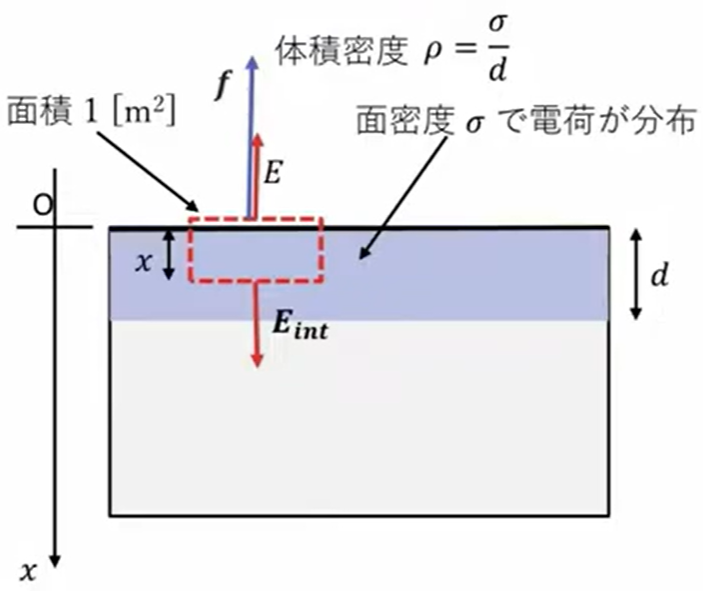
これを具体的に計算してみますと、単純にこれは乗数と\(x\)の一次式の積分なので、難しい積分は全然ございません。どんどん積分していって計算してあげると、次のようになります。

はたらく力は
\(f \ = \displaystyle \int_{0}^{d} \ ρE_{int}dx \ = \ \displaystyle \int_{0}^{d} \ ρ(\frac{ρx}{ε_0} – \frac{ρd}{ε_0}) \ dx \ = \left[ \frac{ρ^2}{2ε_0}x^2 \ – \ \frac{ρ^2 d}{ε_0}x\right]^d_0 \ = \ \frac{ρ^2}{2ε_0}d^2 \ – \ \frac{ρ^2}{ε_0}d^2\)
\(= \left[ \frac{ρ^2}{2ε_0}x^2 \ – \ \frac{ρ^2d}{ε_0}x \right]^d_0 \ = \frac{ρ^2}{2ε_0}d^2 \ – \ \frac{ρ^2}{ε_0}d^2\)
\(= \ -\frac{σ^2}{2ε_0}\)

答えはマイナスになります。今、図のように下向きに\(x\)軸の正方向を取ったので、マイナスということは外向きですね。「外向きに\(\frac{σ^2}{2ε_0}\)」という力が働きます。

これが、電磁気学の教科書で「金属の表面に働く力は\(f=\frac{a^2}{ε_0}\)ですよ」と書いてあるんですが、で電場の大きさは\({σ}{2ε}\)ですよと書いてあるんですが、「これがなんでか」書いてある教科書がなかなかないんです。

僕も1時間「何でここに2がつくの」と考えたことがありました。「\(\frac{σ^2}{ε_0}\)じゃないの？」というふうに勘違いしやすいのですが、それがなぜ「力がこのようになるのか」というのを、計算するということで示してみました。

無限に広い一様な平面上電荷

じゃあ具体的に、基本的な電荷配置について、いくつかガウスの法則を用いて、電場あるいは電位を計算していきましょう。

まず1番目の基本的な配置です。

無限に広い一様な平面上の電荷、綿密度\(σ\)で電荷している面があります。上の図では線で書いていますが「面がある」というふうになります。

このような時の電場をまず計算してみます。

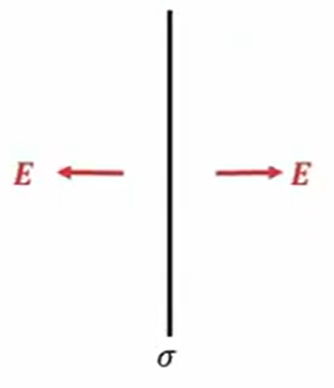
この時は、対称性より電場は左右両方向に同じ大きさで面に垂直に出ています。これは全部、平行になります。ここ1本しか書いていませんが、全部電場こういうふうに平行に出ていきます。

このような状況で、下図の破線で囲んだ単位面積\(dS\)を考えて、この領域にガウスの法則を適用します。

そうすると、まず右辺の中にある電荷量はこれだけの電荷があるわけですから、面密度\(σ\)なので、\(σ\)の\(dS\)かけた電荷量があると。これが総電荷量になります。

\(2EdS \ = \ \frac{σdS}{ε_0}\)

なのでそれを\({ε_0}\)で終わったものが右辺になります。

出ていく電気力線の本数の総量は、左からも右からも\(EdS\)出ていきますので、\(2EdS\)も出ていきます。

これを計算してあげると、この場合の電場の大きさは

\(E \ = \ \frac{σ}{2ε_0}\)

で一定ということになります。要するに、高校の物理などで「均等な電場」って言ってるやつです。単位面積あたりにシグマがある電場の大きさは、このように計算できます。

まとめ：無限に広い一様な平面上電荷 🔵対称性より電気力線は平面に垂直で、みな平行 \(2EdS \ = \ \frac{σdS}{ε_0}\) \(E \ = \ \frac{σ}{2ε_0}\)

面密度 ＋σ、－σの平行平面状電荷分布

次に、今度は2枚の平面状です。

\(+σ\)、\(-σ\)の2枚が電荷です。これは平行平板コンデンサの電荷配置なんですが 、この時の電場を求めるということを考えていきます。

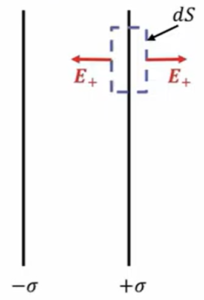
先ほどの面密度と同じように、まずプラスの方面に、破線で囲われた領域にガウスの法則を適用します。

これは先ほど同じで、この時の電場を\(E_+\)としておきますと、\(2E+dS\)が左辺、これが出ていく電気力線の総数、で右辺はここにある電荷の総数を\(ε_0\)割ったものですから、このような形になると。

\(2E_+dS \ = \ \frac{σdS}{ε_0}\)

これから\(E_+\)は、\(\frac{σ}{2ε_0}\)で、電場の向きはこっち向きです。

\(E_+ \ = \ \frac{σ}{2ε_0}\)

赤の矢印で書いた向きということがわかります。

じゃあ今度はマイナスの方にも同じように、ガウスの法則を適用してあげます。

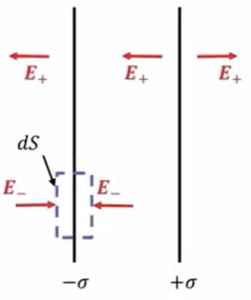
この場合は、ここ（\(-σ\)）にマイナスの電荷があるから、電場の向きはここに向かって入ってくる方向になります。ここで展開してやると、

\(-2E \_ dS \ = \ \frac{-σdS}{ε_0}\)

これ、最初にマイナスが何でついてるかというと、閉曲面があって、「それから出ていくときをプラス」というふうに定義しているためです。この場合は閉曲面に入る方向ですね。両方ともに入る方向なので、そのために\(2E\)にマイナスがついています。

それで中にある総電荷量が\(-σ\)で、面積\(dS\)に分布してるわけですから、総電荷量はこのような形になって、同じようにこの\(E \_ \)の大きさとしては、

\(E_{-} \ = \ \frac{σ}{2ε_0}\)

となります。なので、具体的にはこの2つの場合の重ね合わせ＝足し算ということになりまして、

中間で　\(E \ = \ E_+ \ + \ E_{-} \ = \ \frac{σ}{ε_0}\)

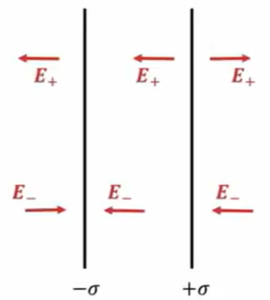
このようになって、電極と電極の間では\(E+\)と\(E_{-}\)を足したもの、向きは左向きということで、これを足し算すると\(\frac{σ}{ε_0}\)という電場がはたらいているということになります。

じゃあ外側では、図の左側でも右側でも同じなのですが、矢印の右向きと左向きがそれぞれを相殺している＝キャンセルしています。\(E+\)と\(E_{-}\)は大きさなので、外側では電場は0です。この場合には「電場がありません」ということになります。

外側で　\(E \ = \ \pm E_+  \mp \ E_{-} \ = \ 0\)

これが実はこの中間のところの電場っていうのは、平行平板コンデンサーの極板間に働いている電場の大きさと同じです。

まとめ：面密度\(+σ\)、\(-σ\)の平行平面状電荷分布 \(2E_+dS \ = \ \frac{σdS}{ε_0}\) \(E_+ \ = \ \frac{σ}{2ε_0}\) \(-2E \_ dS \ = \ \frac{-σdS}{ε_0}\) \(E \_ \ = \ \frac{σ}{2ε_0}\) 中間で　\(E \ = \ E_+ \ + \ E_- \  = \ \frac{σ}{ε_0}\) 外側で　\(E  \ = \ \pm E_+ \ \mp E_- \ = \ 0\)

表面に一様に帯電した無限長導体円

3つ目の例です。

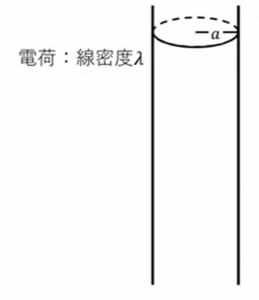
今度は筒円です。筒状で、表面のみに電荷が分布しています。この時の電場を考えてみます。

電荷の密度としては線密度で表しまして、長さ1メートルあたり\(λ\)の電荷量で分布していて、筒の半径はA、この時の電場はどうなるんでしょうか、ということを計算してみます。

まず外側ですが、下図のように、赤の破線で書いたような円筒を考えて、この部分にガウスの法則を適用します。

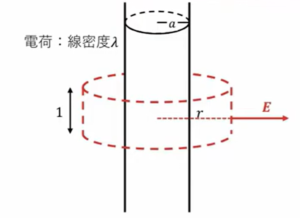
そうすると出ていく電場をEとします。これは対称性から、等方的にどの向きにも同じように出ていきますので、この側面積を計算していけばいいわけです。

そうすると半径\(r\)なので、高さ1の円筒を考えてますので、周囲の長さが\(2π・E\)ということになります。

この中にある電荷の総量は、1mあたり\(λ\)の電荷があって、今1mを考えてるわけですから総量は\(λ\)になります。

なので、ガウスの法則の積分型に落としてやるとこのような形になります。

円筒外部\((r \ ≧ \ a)\)で
\(2πr・E \ = \ \frac{λ}{ε_0}\)

なので、これから電場を求めてやると、\(r\)より外側では\(\frac{λ}{2πε}\)となります。

\(E \ =  \frac{λ}{2πε_0r} \ (r \ ≧ \ a )\)

この場合はこのような電場がはたらくことになります。

ついでに、電位もちょっと計算してみます。電位は前も学習したように、\(E\)を積分したものにマイナスを付けたものが電位でした。

これを積分してあげると次のような形になります。

\(V \ = \ – \displaystyle \int Edr \ =  \ – \frac{λ}{2πε_0} \ log \ r \ + \ C\)

Cは積分乗数です。

今までの点電荷などの場合は、無限遠を基準点において0として電場を計算したので、積分乗数は出てこなかったのですが、このようにこの場合は電位の形が\(-\frac{λ}{2πε_0}log \ r\)と、こんな形になってしまうので、\(r\)を無限大に追って行った時に、電位の大きさは0にならない。そこを基準とするわけにいかないので、積分乗数という形でもってきます。

この積分乗数は、他の条件によって具体的に定まることになります。例えば、この筒状の電位が\(V1\)ボルトだったとすると、それによって\(C\)が定まっていくということになります。

では筒の内側を考えていきます。

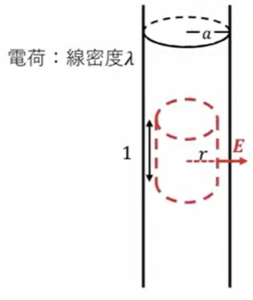
筒の内側に、今度はこのような円筒面で閉曲面を考えて、ガウスの定理を考えます。

出ていく電場の大きさ\(2πr・E\)は同じなのですが、今は筒状の外側の壁のみに電荷が分布しているということを考えてますので、この中に電荷はありません。なので右辺の電荷量は0ということになります。なのでガウスの定理はこのような形になります。

円筒内部\((r \ < \ a \ )\) で
\(2πr・E \ =  \frac{0}{ε_0}\)
\(E = \ 0\)

結果、筒の内側では電場は0、ということになります。で、電位を計算すると電場が0、傾きがあるので\(V\)は一定値となります。

\(V \ = \ 一定\)

これが筒状の表面に電荷が分布した場合の電場計算です。

まとめ：表面に一様に帯電した無限長導体円筒 円筒外部\((r \ ≧ \ a )\)で \(2πr・E \ = \ \frac{λ}{ε_0}\) \(E \ = \ \frac{λ}{2πε_0r}\)　\((r \ ≧ \ a)\)　　　\(V \ = \ -\displaystyle \int Edr \ = \ -\frac{λ}{2πε_0} \ log \ r \ + \ C\) 円筒内部\((r \ < \ a)\)で \(2πr・E \ = \ \frac{0}{ε_0}\) \(E \ = 0\)　　　\(V \ = \ \)一定

一様に帯電した導体球殻

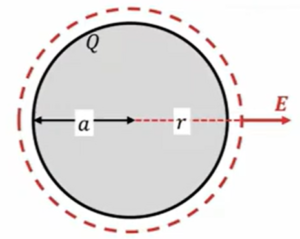
その次の例として、今度は一様に帯電した球体を考えます。

球の表面だけに電荷が存在していて、球の内側には電荷はありません。このような場合の電場がどうなりますか、という問いです。これは教科書にもよくある例なのですが、これを考えていきます。

電荷の総量としては\(Q\)ということを考えておきます。\(Q\)の半径は\(a\)です。

これも同じように、まず外側の電場を計算しますので、外側に半径\(r\)の\(Q\)の領域を持つ閉曲面を考えます。

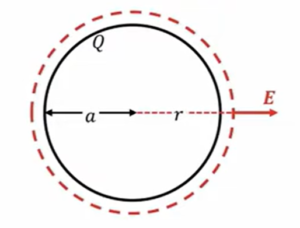
この場合も電場は対称性から考えて、\(Q\)は一様に分布しているわけですから、どっちの向きも同じでありまして、対称に出ていきます。

そうすると、球の表面積は\(4πr^2\)なので、表面積\(4πr^2\)に電場をかけたもの、これだけの電気力線数が出ていくということで、次のようになります。

球殻外\((r \ > \ a)\)
\(4πr^2・E \ = \ \frac{Q}{ε_0}\)

右辺は、破線の中にある総電荷量を\(ε_0\)=「真空の融点率」で割ったものですから、この中には\(Q\)の電荷があるわけですから、\(Q÷ε_0\)ということになります。従って、電場の大きさは\(Q\)の外側では、

\(E \ = \ \frac{Q}{4πε_0r^2} \ (r \ > \ a )\)

ということになります。

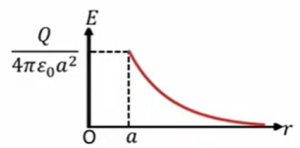
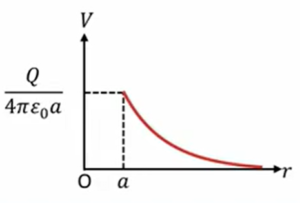
これはどこかで見た形でして、つまり\(Q\)が球殻の中心に点電荷として存在する場合の電場と同じですよ、ということを言っているわけです。なので具体的にグラフにして表してみると、

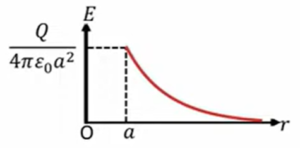
このような\(\frac{Q}{4πε_0a^2}\)、\(r\)は無限大のところで、だんだん0に近づいてくると大きくなって、こんな形になっています。

で電位を計算しますと、この場合は無限大が0なので、電位計算は電場を無限大から\(r\)まで積分してマイナスつけてやればいいということになります。そうすると\(\frac{Q}{4πε_0r}\)ということになるので、このような形になります。

\(V \ = \ – \displaystyle \int_{∞}^{r} \ Edr \ = \ \frac{Q}{4πε_0r}\)
\(V(a) \ = \ \frac{Q}{4πε_0a}\)

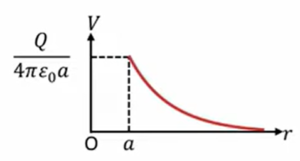
そうすると球殻のところ、半径\(r\)のところの電位はどうなりますかというと、この\(r\)に\(a\)を代入してやればいいわけですから\(V(a)\)で計算すると、球殻なので\(\frac{Q}{4πε_0}\)ということで電位は球殻の外側ではこのような変化をします。

じゃあ内側ではどうなのかというと、次のように考えます。

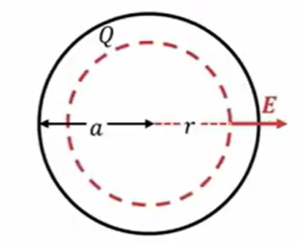
内側でも同じようにガウスの法則を適用してあげます。

球殻内\((r \ < \ a)\)
\(4πr^2・E \ = \ \frac{0}{ε_0}\)

そうすると同じように、左辺は出ていく電場量は半径\(r\)の球面から出ている電場と考えるわけですから、\(Q\)の表面積\(4πr^2\)に電場を掛けたもの、これが電気力線の総数です。

今度はこの赤の球内を考えますが、電荷の外側の球殻のみに存在してるわけですから、この赤点線の中には電荷はありません。0です。なので右辺の電荷量は0になって、ガウスの法則は

\(4πr^2・E \ = \ \frac{0}{ε_0}\)

のような形になります。つまり半径の内側では電場はゼロですということになります。

\(E \ = \ 0 \ (r \ < \ a)\)

電場はこのような変化をしているわけです。

そうすると電場が0なので電位は一定なのですが、どのように一定値を取るのかというと、このように連続性がありますので、

ここでも成り立たなければいけないのでここと同じ電場になります。

つまり電位は、無限遠に向かって0で、球殻に向かってどんどん大きくなっていくんですが、球殻のところで一定値になると電場の大きさは内側では一定になります。

電場の大きさは内側では0になり、球殻上に電荷が分布している場合はこのような形になります。

\(V \ = \ V(a) \ = \ \frac{Q}{4πε_0a}\)

これは先ほども言いましたけど、よくよく教科書に載っている例題のケースです。

まとめ：一様に帯電した導体球殻 球殻外 \((r \ > \ a \ )\) \(4πr^2・E \ = \ \frac{Q}{ε_0}\) \(E \ = \ \frac{Q}{4πε_0r^2} \ (r \ > \ a)\)　　\(V \ = \ -\displaystyle \int_{∞}^{r} \ Edr \ = \ \frac{Q}{4πε_0r}\) \(V(a) \ = \ \frac{Q}{4πε_0a}\) 球殻内\((r \ < \ a)\) \(4πr^2・E \ = \ \frac{0}{ε_0}\) \(E \ = \ 0　\ (r \ < \ a) \ \ V \ = \ V(a) \ \frac{Q}{4πε_0a}\)

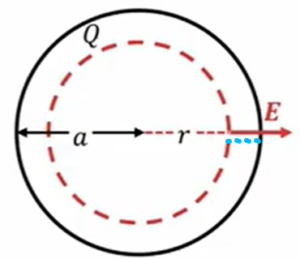
一様に\(Q\)に帯電した導体球

じゃあ、同じ球殻なのですが、今回は球殻全体に一様に分布している点が、外側だけじゃなくて内側（下図の灰色の部分）にも電荷が一様に分布してトータル\(Q\)の変化が分布している場合です。

 

この場合はどうなるのかを、今度は考えていきます。

まず外側ですが、ここで書いたように球の外側に半径\(r\)の球面を考えて、それに対するガウスの法則を考えてあげます。

そうすると球の表面積\(4πr^2\)に電場の大きさをかけたものが出ていく電気力線の総数になりますので、左辺は\(4πε^2・E\)。で、この赤点線の中に含まれる電荷の総量は\(Q\)になるので、\(\frac{Q}{ε_0}\)となります。なので電場の大きさは\(\frac{Q}{4πε_0r^2}\)となります。

\(E \ = \ \frac{Q}{4πε_0r^2} \ (r \ > \ a)\)

これは球殻に\(r\)倍をしたのと全く同じ形をしています。なので、電位も同じように計算してやると、\(\frac{Q}{4πε_0r}\)で、\(a\)のところの電位は同じです。

\(V(a) \ =  \frac{Q}{4πε_a}\)

ここは外側に関しては球殻に電荷があった場合、先ほどの計算例と同じわけです。

じゃあ内側の電場はどうなるのかというと、これは先ほどとちょっと変わってきまして、このように球体の内側に半径rの球面を考えます。

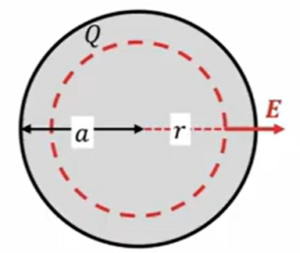
ここでガウスの法則を適用しますと、やっぱり表面積は\(\frac{E}{4πr^2}\)となります。

ただし、この赤の破線の球面の中にある電荷量はどうなるのかというと、半径\(r\)の中にある電荷量になるわけですから、球の電荷量は\(\frac{r^3}{a^3}\)になるわけですね。

つまり全体には\(\frac{4}{3}πa^3\)という体積上に均等に分布しているわけですが、この半径\(r\)を書いてきた時はそのうちの\(\frac{4}{3}πr^3\)にある部分が、赤の破線の中の電荷量しかないわけですから、これを比を取って\(\frac{r^3}{a^3}\)という形になって、ここが先ほどと変わってきます。

球殻内\((r \ < \ a)\)
\(4πr^2・E \ = \ \frac{1}{ε_0} \frac{r^3}{a^3}Q\)
\(E \ = \ \frac{1}{4πε_0} \frac{Qr}{a^3}(r \ < \ a)\)

そうすると電場の大きさはこのように計算できて、実は\(r\)に比例するような形になっているということで、ここに書きましたように\(r\)に比例するような電場をしてます。

先ほど球殻にある場合は、ここは0でした。

これを積分してあげますと、これは\(V(a)\)に\(a\)から\(r\)まで電場を積分したものによって電場を求められるわけですから、これは素直にどんどん計算していきます。

\(V \ = \ V(a) \ – \displaystyle \int_{a}^{r} \ Edr \ = \ \frac{Q}{4πε_0a}\)
\(= \ \frac{Q}{4πε_0a} \ – \ \frac{Q}{4πε_0a^3} (\frac{r^2 \ – \ a^2}{2})\)

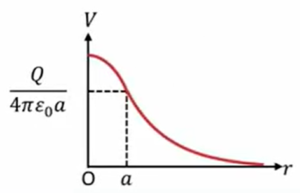
\(\frac{1}{r^1}\)の積分なのでややこしい式も入ってないため、積分していくとこのような形になり、さらに電位が放物線上に\(r^2\)に比例するような形で上がっていく、このような電位を持つということになります。

この場合、先ほどの図ですが、

こちらはよく教科書などその辺りで見かけます。ですが次に紹介したこちらの図の方、\(V\)に近い部分の電位分布（赤線）が「このような形になるんですよ」って書いたものは意外と少ないです。

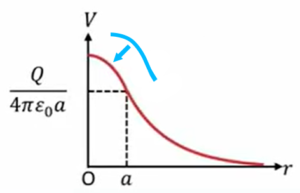
実はあまり見かけません。実は電位分布としては、この場合はこのような形になります。

まとめ：一様に\(Q\)に帯電した導体球 球殻外\((r \ > \ a)\) \(4πr^2・E \ = \ \frac{Q}{ε_0}\) \(E \ = \ \frac{Q}{4πε_0r^2} \ (r \ > \ a) \ \ \ \ \ V \ = \ – \displaystyle \int_{∞}^{r} Edr \ = \ \frac{Q}{4πε_0r}\) 球体内\((r \ < \ a)\) \(4πε^2・E \ = \ \frac{1}{ε_0} \frac{r^3}{a^3}Q\) \(E \ = \ \frac{1}{4πε_0} \frac{Qr}{a^3}(r \ < \ a) \ \ \ \ V \ = \ V(a) \ – \ \displaystyle \int_{a}^{r} Edr \ = \ \frac{Q}{4πε_0a}\) \( = \ \frac{Q}{4πε_0a} \ – \ \frac{Q}{4πε_0a^3}(\frac{r^2 \ – \ a^2}{2})\)

例題

他にも計算できる電荷分布の例はあるのですが、ここまで代表的な例を見てきました。

最後に今回のまとめとして、もうちょっと複雑なケースの計算をして、例題とします。

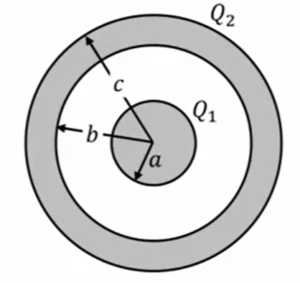
半径\(a\)の導体球を内半径\(b\)、外半径\(c(a \ < \ b \ < \ c)\)の導体球殻で包み、内球に\(Q_1\)、外球に\(Q_2\)の電荷を与えた場合の電場と内球、外球の電位を求めよ。

ここにありますように、半径\(a\)の導体球と、内半径\(b\)、外半径\(c\)の導体球、これが同心円球状に2つ並んでます。

内側の球体に電荷\(Q_1\)を与え、外側の球殻には\(Q_2\)を与えました。この時に、電場の大きさ、あるいは内球、外球の電位の大きさはどうなるかということを計算しなさいという例題です。

これも実はガウスの法則を適用することによって、比較的計算はできます。それを見ていきたいと思います。

まず最初にやることは、ガウスの定理を適用する領域を、次のように外側の球の導体内部にとってみることを考えます。

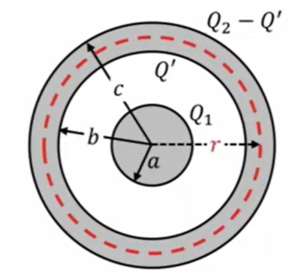
そうすると今回の最初にやったように、導体の内部では電場は0なので、ガウスの法則の左辺は\(4πr^⁠2\)（球の表面積）、そこに電場は0ということになります。

この中にある電場は、この外殻に\(Q’\)の電荷が存在するというふうに仮定すると、電荷保存則、電荷量\(Q_2\)を与えたわけですから、外側の表面には\(Q_2 \ – \ Q’\)という、これだけの電荷がいるということになります。

ということを考えると、この赤の点線の中にある総電荷量は、この場合は\(Q_1+Q’\)ということになります。

すると左辺が0なので、\(Q’\)は\(-Q_1\)ということになります。

外球内面の電荷を\(Q’\)とすると
\(4πr^2・0 \ = \ \frac{Q_1 \ + \ Q’}{ε_0}\)　⇒\( \ (Q’ \ = \ -Q_1\)　⇒　外球の外面の電荷は\(-Q_1 \ + \ Q_2\)

つまり、ここに\(Q_1\)があった時に、ここに外側の内面に誘導される電荷は\(-Q_1\)ですよと。

外側にはトータルの電荷量が\(Q_2\)っていうのは変わらないので、\(Q_1+Q2\)ですよと。まずこのような金属表面に電荷分布が入るということが、ガウスの定理を外側の金属の内部に持ってくることによってまずわかります。

これで各金属表面にある電荷がわかったわけですから、ガウスの法則をどんどん外側から適用していき ます。

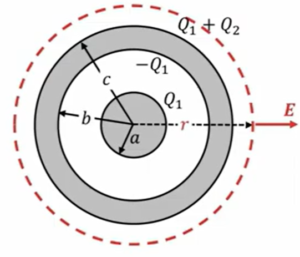
まず1番外側の球体にある場合、この領域にガウスの法則を適用すると、球面の球の表面積が\(4πr^2\)、電場の大きさが\(E\)なので\(4πr^2\)に\(E\)を掛けます。

外側の波線の領域にある電荷量は、これの持ってる電荷量の総和なので、\(Q_1+Q_2\)になります。

なので、この場合の電場は外側で\(\frac{Q_1 \ + \ Q_2}{4πε_0r^2}\)です。

外球の外側\((r \ > \ c)\)で
\(4πr^2・E \ = \frac{Q_1 \ + Q_2}{ε_0}\)　⇒　\(E \ = \frac{Q_1 \ + Q_2}{4πε_0r^2}\)

電位は、これを無限大から\(r\)まで積分してマイナスをつけたものを計算してやればいいわけですから、次のようになります。

\(V(r) \ = \ – \displaystyle \int_{∞}^{r} \ Edr \ = \frac{Q_1 \ + \ Q_2}{4πε_0r}\)

これが外側の電場です。

これで電場が計算できたので、電位が計算できるわけです。ここの中では電位はすべて一緒ですので、\(r\)が\(c\)の時の電場を計算すればいいわけでして、それは図の灰色の中だったらどこでも等電位（金属の導体のため）なので、\(V(b)\)も\(V(c)\)も同じで、この場合はこの\(r\)を\(c\)に持ってきたもの、\(\frac{Q_1 \ + Q_2} {4πε_0c}\)、これが外側の球体の電位ということになります。

外球表面の電位
\(V(b) \ = \ V(c) \ = \frac{Q_1 \ + \ Q_2}{4πε_0c}\)

では次に、内側の球体と外側の球体の内部を考えます。

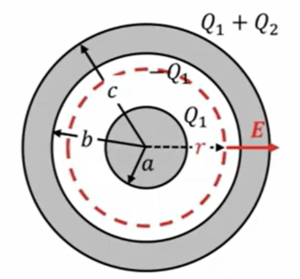
ここの図の赤の破線で書いたような領域を持ってきて、ガウスの法則を適用していきます。

そうすると。左辺はやっぱり同じで\(4πr^2・E\)になりますが、今度は考えてる閉曲面が赤い破線の円ですので、ここの中にある電荷は\(Q_1\)しかありません。なので左辺は\(\frac{Q_1}{ε_0}\)ということになります。

なので、この領域での電場は\(E \ = \ \frac{Q_1}{4πε_0r^2}\)です。

内球と外球の間\((a \ < \ r \ < \ b)\)で
\(4πr^2・E \ = \ \frac{Q_1}{ε_0}\)　⇒　\(E  \ = \ \frac{Q_1}{4πε_0r^2}\)

そうするとここの電場は、ここの\(V(b)\)の電位から下図の青い矢印の範囲を積分してきたものを求めればいいわけです。

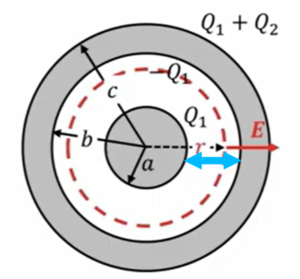
\(V(b)\)に\(-b\)から\(a\)まで\(E\)を積分したものを計算しますと、これも難しい積分の数学が入っていませんので、このような形に表せます。

\(V(r) \ = \ V(b) \ – \displaystyle \int_{b}^{r} \ Edr \ = \ \frac{Q_1}{4πε_0} \ (\frac{1}{r} \ – \ \frac{1}{b}) \ + \ \frac{Q_1 \ + \ Q_2}{4πε_0c}\)

そうすると、最後にこの内側の電位ですが、\(V(r)\)は青矢印で示した、間の電位を計算したやつなので、これに\(r\)を\(a\)にすると内側の電場っていうのは求めることができまして、\(V(a)\)はここの\(r\)に\(a\)を入れてやればいいです。なので、次のような形に表すことができます。

\(=\frac{Q_1}{4πε_0c} (\frac{1}{a} \ – \ \frac{1}{b} \ + \ \frac{1}{c}) \ + \frac{Q_2}{4πε_0c}\)

なのでまとめますと、\(Q\)の外側での電場の大きさは\(E \ = \ \frac{Q_1 \ + \ Q_2}{4πε_0r}\)です。で、外側の灰色や中心部分の灰色のところは導体内なので電場は0です。

この中間部分での電場の大きさは\(E \ = \frac{Q_1}{4πε_0c}\)です。外側の導体球の電位の大きさは\(\frac{Q_1 \ + \ Q_2}{4πε_0c}\)です。内側の導体球の電位の大きさは\(\frac{Q_1}{4πε_0}(\frac{1}{a} \ – \ \frac {1}{b} \ + \ \frac{1}{c}) \ + \ \frac{Q_2}{4πε_0c}\)です。

というのが、求めるべき答えということになります。

おわりに

以上、今回は、前回やったガウスの法則を用いて、いくつかの基本的電荷配置について、電場をどう計算しているかというのを見てみました。

そして最後にちょっと複雑な例として、2つの導体球がある場合の電場での計算、ということを例題として扱いました。

以上です。

↓動画版はこちら！
江口和弘講師：「【大学物理】電磁気学 第5回 – Gaussの法則を用いた電場計算」（所要時間 31:48 ）